度限制最小生成树和第K最短路算法

目录

一、最小生成树和第K最短路算法介绍

二、最小生成树和第K最短路算法原理

1、最小生成树算法原理

1.1、普里姆(Prim)算法

? ? ? ?1.1.1 算法原理：

? ? ? ?1.1.2 实现过程：

? ? ? ? ? ? ?1.1.3??算法代码实现：

1.2、克鲁斯卡尔(Kruskal)算法

? ? ? ? ?1.2.1 算法原理：

? ? ? ? ?1.2.2?算法实现过程： ?

1.2.3?算法代码实现

2、最短路径算法原理

2.1、单源最短路径

? ? ? ? 2.1.1 算法原理

?????????2.1.2?算法实现过程：

? ? ? ??2.1.3 算法代码实现

2.2、Bellman-Ford 和 SPFA 算法 ? ? ??

????????2.2.1 算法原理

? ? ? ? 2.2.2??Bellman-Ford 算法过程：

? ? ?2.2.3 算法代码实现

2.3、Floyd算法

2.3.1 算法原理

2.3.2 其步骤如下

2.3.3 代码实现?

三、总结

---

一、最小生成树和第K最短路算法介绍

????????在一个加权无向图中，最小生成树（Minimum Spanning Tree，MST）指的是一棵包含图中所有顶点的树形结构，它包含的边的总权重最小。最小生成树在网络设计、电路设计等领域有广泛应用。最常用的最小生成树算法有Prim算法和Kruskal算法。

二、最小生成树和第K最短路算法原理

1、最小生成树算法原理

1.1、普里姆(Prim)算法

????????一个含有n个顶点的连通图G，若它的一棵带权生成树的各边权值之和最小，则称该生成树为图G的最小生成树，该树包含图的所有顶点，其边的个数为n-1；在生成最小生成树时可以选择不同的边，所以最小生成树不唯一（存在权值相同的边）；但若当图G的各边权值不同，则此时最小生成树是唯一的。

? ? ? ?1.1.1 算法原理：

????????此算法可以称为“加点法”，每次迭代选择代价最小的边对应的点，加入到最小生成树中。算法从某一个顶点s开始，逐渐长大覆盖整个连通网的所有顶点。

? ? ? ?1.1.2 实现过程：

????????(1).令所有点的集合为V，任选一个点的的集合为U,未选到的点集合为V-U=VV；
????????(2).在U和VV两个集合能组成的边中选一条权值最小的边加入到生成树中，并且更新集合；
????????(3).重复2的过程，直到所有点包括到生成树里或者生成树有n-1条边；??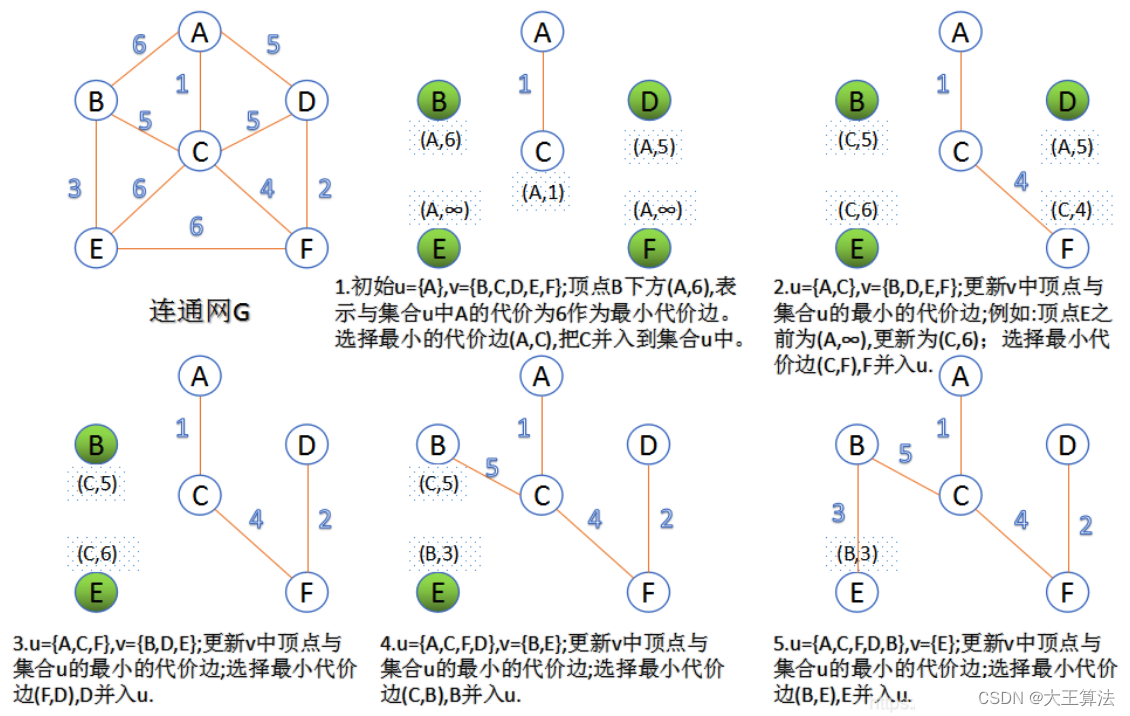

? ? ? ? ? ? ?1.1.3??算法代码实现：

#include<iostream>
#include<string.h>
#include<algorithm>
#include<math.h>
#include<stack>
#include<map>
#include<queue> 
#include<vector>
#include<set>
#define ll long long 
#define INF 0x3F3F3F3F 
#define MOD 1000000007

using namespace std; 
const int MAXN=2e5+7;
int a[3010][3010],,d[3010],n,m,ans;
bool vis[3010];
bool prime(){
	memset(d,0x3F3F3F3F,sizeof(d));
	memset(v,0,sizeof(v));
	d[1] = 0;
	for(int i =1 ;i < n ;i++){
		int x = 0;
		for(int j = 1;j <= n;j++){
			if(!v[j] && (x == 0 || d[j] < d[x])){
				x = j;
			}
		}
		v[x] = 1;
		for(int y = 1;y <= n;y++){
			if(!v[y])d[y] = min(d[y],a[x][y]);
		}
	}
}
int main()
{
	cin>>n>>m;
	memset(a,0x3F3F3F3F,sizeof(a));
	for(int i = 1;i <= n;i++){
		int x , y,z;
		cin>>x>>y>>z;
		a[y][x] = a[x][y] = min(a[x][y],z);
	}
	prime();
	for(int i =2;i<=n;i++){
		ans += d[i];
	}
	cout<<ans<<endl;
	return 0;
}

1.2、克鲁斯卡尔(Kruskal)算法

????????一个含n个顶点的图，克鲁斯卡尔算法的思想是将图的所有边对应的权值按照从小到大的顺序依次开始选取，若选取的某边与先前的树构成回路，则舍去，一直进行下去，直到所有顶点被访问到，当生成树的边的个数为n-1时为止，即可得到最小生成树。

? ? ? ? ?1.2.1 算法原理：

????????此算法可以称为“加边法”，初始最小生成树边数为0，每迭代一次就选择一条满足条件的最小代价边，加入到最小生成树的边集合里。这是一个贪心的过程。? ?

? ? ? ? ?1.2.2?算法实现过程： ?

? ? ? ? (1).首先把所有的边权从小到大排序；
????????(2).把图中的n个顶点看成独立的n棵树组成的森林；
????????(3).选出权值最小两个点形成的边，u，v(u，v应属于不同的树),加入到生成树中；
????????(4).重复3的过程，直到所有点包括到生成树里或者生成树有n-1条边；?

1.2.3?算法代码实现

#include <vector>
#include <algorithm>

// 定义边的结构体
struct Edge {
    int src, dest, weight;
};

// 用于排序的比较函数
bool compareEdge(Edge a, Edge b) {
    return a.weight < b.weight;
}

// 查找集合的根并进行路径压缩
int find(std::vector<int>& parent, int i) {
    if (parent[i] != i)
        parent[i] = find(parent, parent[i]);
    return parent[i];
}

// 按秩合并两个集合
void unionSets(std::vector<int>& parent, std::vector<int>& rank, int x, int y) {
    int xroot = find(parent, x);
    int yroot = find(parent, y);

    if (rank[xroot] < rank[yroot])
        parent[xroot] = yroot;
    else if (rank[xroot] > rank[yroot])
        parent[yroot] = xroot;
    else {
        parent[yroot] = xroot;
        rank[xroot]++;
    }
}

// Kruskal算法主函数
std::vector<Edge> kruskalMST(std::vector<Edge>& edges, int V) {
    std::vector<int> parent(V);
    std::vector<int> rank(V, 0);
    std::vector<Edge> result;

    // 初始化每个顶点的集合
    for (int i = 0; i < V; ++i)
        parent[i] = i;

    // 按照边的权重排序
    std::sort(edges.begin(), edges.end(), compareEdge);

    for (Edge e : edges) {
        int x = find(parent, e.src);
        int y = find(parent, e.dest);

        // 如果加入这条边不会形成环
        if (x != y) {
            result.push_back(e);
            unionSets(parent, rank, x, y);
        }
    }

    return result;
}

2、最短路径算法原理

2.1、单源最短路径

? ? ? ? 2.1.1 算法原理

????????单源最短路径(single source shortest path ,SSPP问题),给定一张有向图G = (V,E），V是点集，E是边集，| V | = n ,| E | = m ，节点以[1,n]之间的连续整数编号，(x,y,z)表示一条从x出发，到达y，长度为z的有向边。设点1为起点，dist[i]表示从起点1到节点i的最短路径的长度。

?????????2.1.2?算法实现过程：

????????(1).初始化 dist[1]=0,其余节点的dist值为INF(无穷大);
????????(2).找出一个未被标记的，dist[x] 最小节点 x，然后标记节点x；
????????(3).扫描节点x的所有出边(x,y,z)，若dist[x]+z < dist[y]，则使用 dist[x]+z 更新dist[y];
????????(4).重复上述2-3的步骤，知道所有节点被标记；?

? ? ? ??2.1.3 算法代码实现

#include<iostream>
#include<string.h>
#include<algorithm>
#include<math.h>
#include<stack>
#include<map>
#include<queue> 
#include<vector>
#include<set>
#define ll long long 
#define INF 0x3F3F3F3F 
#define MOD 1000000007

using namespace std; 
const int MAXN=2e5+7;
int a[3010][3010],d[3010],n,m;
bool v[3010];
void dijkstra(){
	//初始化dist，v数组
	memset(d,0x3f,sizeof(d));
	memset(v,0,sizeof(v));
	d[1] = 0;
	for(int i =1;i<n;i++){
		//找出未标记节点中dist最小的
		int x = 0;
		for(int j = 1;j<=n;j++){
			if(!v[j] && (x == 0 || d[j] < d[x])){
				x == j;
			}
		}
		v[x] = 1;
		//用全局最小节点x更新其他节点
		for(int y = 1; y<= n;y++){
			d[y] = min (d[y],d[x]+a[x][y]);
		}
	}
}
int main()
{
	cin >> n >>m;
	memset(a,0x3f,sizeof(a));
	//构建邻接链表
	for(int i =1;i<=n;i++){
		a[i][i] = 0;
	}
	for(int i = 1;i<=m;i++){
		int x,y,z;cin>>x>>y>>z;
		a[x][y] = min(a[x][y],z);
	}
	dijkstra();
	for(int i =1;i<=n;i++){
		cout<<d[i]<<endl;
	}
	return 0;
}
//以上可用二叉堆对dist数组进行维护，可在o(m*log n)时间内实现

2.2、Bellman-Ford 和 SPFA 算法 ? ? ??

????????2.2.1 算法原理

?????????给定一张有向图，若对图中的某一条(x,y,z)，有dist[y]<=dist[x]+z成立，则该边慢走三角形不等式。若所有的边都满足三角形不等式，则dist数组就 是所求的最短路。

? ? ? ? 2.2.2??Bellman-Ford 算法过程：

? ? ? ?1).扫描所有边(x,y,z),若dist[y] > dist[x]+z，则用 dist[x]+z更新dist[y]
? ? ?? 2).重复上述步骤，知道没有更新操作发生。
? ? ? ?Bellman-Ford 算法时间复杂度o(mn)
? ? ? ?SPFA 算法就是“队列优化的 Bellman-Ford 算法”
? ? ? ?过程
? ? ?1).建立一个队列，最初队列中只含有起点1；
? ? ?2).取出队列头部节点x，扫描它的所有出边(x,y,z),若dist[y] > dist[x]+z，则用 dist[x]+z更新dist[y].同时，若y不在队列中，则把y入队。
? ? ?3).重复上述步骤，知道队列为空。
?????时间复杂度o(km),k为一个随机常数，但特殊构造的图上，很有可能退化成o(n*m)。?

? ? ?2.2.3 算法代码实现

#include<iostream>
#include<string.h>
#include<algorithm>
#include<math.h>
#include<stack>
#include<map>
#include<queue> 
#include<vector>
#include<set>
#define ll long long 
#define INF 0x3F3F3F3F 
#define MOD 1000000007

using namespace std; 
const int MAXN=2e5+7;
const int N = 100010, M = 1000010;
int head[N],ver[N],edge[M],Next[M],d[N];
int n,m,tot;
queue<int>q;
bool v[N];
void add(int x,int y,int z){
	ver[++tot] = y;edge[tot] = z;
	Next[tot] = head[x],head[x] = tot;
}
void spfa(){
	memset(d,0x3f,sizeof(d));
	memset(v,0,sizeof(v));
	d[1] = 0,v[1] = 1;
	q.push(1);
	while(q,size()){
		int x = q.front();q.pop();
		v[x] = 0;
		for(int i = head[x];i;i=Next[i]){
			int y = ver[i],z = edge[i];
			if(d[y] > d[x]+z){
				d[y] = d[x]+z;
				if(!v[y])q.push(y),v[y] =1;
			}
		}
	}
}
int main()
{
	cin >> n >>m;
	for(int i = 1;i<=m;i++){
		int x,y,z;cin>>x>>y>>z;
		add(x,y,z);
	}
	spfa();
	for(int i =1;i<=n;i++){
		cout<<d[i]<<endl;
	}
	return 0;
}

2.3、Floyd算法

2.3.1 算法原理

????????弗洛伊德算法用于求一对顶点之间的最短路径，任意两点间的最短路。

2.3.2 其步骤如下

• 若对于图中的顶点vi和顶点vj，规定若两个顶点之间存在边，则将该边上的权值作为其最短路径长度，否则以∞表示其最短路径长度；
• 然后在每条路径中加入中间顶点，若加入后的路径长度减少了，则新路径替换旧路径，得到新的最短路径长度。
• 动态转移方程：d[k][i][j] = min(d[k-1][i][j],d[k-1][i][k]+d[k-1][k][j])

2.3.3 代码实现?

#include<iostream>
#include<string.h>
#include<algorithm>
#include<math.h>
#include<stack>
#include<map>
#include<queue> 
#include<vector>
#include<set>
#define ll long long 
#define INF 0x3F3F3F3F 
#define MOD 1000000007

using namespace std; 
const int MAXN=2e5+7;
int d[310][310],n,m;

int main()
{
	cin>>n>>m;
	memset(d,0x3F3F3F3F,sizeof(d));
	for(int i =1;i<=n;i++){
		d[i][i] = 0;
	}
	for(int i = 1;i<=m;i++){
		int x,y,z;cin>>x>>y>>z;
		d[x][y] = min(d[x][y],z);
	}
	//floyd算法
	for(k=1;k<=n;k++)  
    for(i=1;i<=n;i++)  
    for(j=1;j<=n;j++)  
    	d[i][j] = min(d[i][j],d[i][k]+d[k][j])
    for(int i =1 ;i<=n;i++){
    	for(int j =1;j<=m;j++){
    		cout<<d[i][j];
    	}
    	puts("");
	}
	return 0;
    
}

三、总结

? ? ??最小生成树算法和第K最短路算法都是图论中的经典算法，它们在网络设计、路由选择等多个领域有着重要应用。这些算法在实际应用中通常需要根据具体问题的特点来选择合适的算法。MST算法着重于构造最小权重的树，而第K最短路算法侧重于寻找多条不同的路径。

?参考资料：

https://wenku.baidu.com/view/535da811edfdc8d376eeaeaad1f34693daef10cc.html?fr=income1-doc-search&_wkts_=1705245210619&wkQuery=%E5%BA%A6%E9%99%90%E5%88%B6%E6%9C%80%E5%B0%8F%E7%94%9F%E6%88%90%E6%A0%91%E5%92%8C%E7%AC%ACK%E6%9C%80%E7%9F%AD%E8%B7%AF%E7%AE%97%E6%B3%95&needWelcomeRecommand=1