整数和浮点数在内存中的存储

数据在内存中的存储

在计算机系统中，数据在内存（RAM - Random Access Memory）中的存储方式取决于数据类型、操作系统、处理器架构以及编程语言等因素。以下是一些关键点来描述数据如何被存储在内存中：

1. 字节寻址:
? ?内存通常是按照字节进行寻址的，这意味着每个内存位置可以保存一个字节（8位）的信息。

2. 连续分配:
? ?当程序声明一个变量时，编译器会为该变量分配一段连续的内存空间。例如，如果声明了一个整型数组 int arr[10]; 并且假设整型占用4个字节，则此数组将占用40个连续的字节。

3. 对齐约束:
? ?出于性能优化和硬件要求的原因，许多处理器对某些数据类型有特定的对齐规则。例如，在32位系统上，可能需要将4字节大小（如整数）放置在地址是4倍数的地方。

4. 大端和小端模式 (Endianness):
? ?不同体系结构可能采用不同方式来表示多字节值：
? ? - 大端模式：高序位（最重要位）保存在低地址处。
? ? - 小端模式：高序位保存在高地址处。
5. 栈与堆:
? ?数据可以存在于两种主要区域之一——栈或堆：
? ? - 栈：函数调用时自动管理局部变量所使用的区域。它具有后进先出(LIFO) 的特性，并且当函数返回时由编译器负责清理。
? ? - 堆：通常由程序员显式分配和释放，并且生命周期不受函数作用域限制。

6. 虚拟内存管理:
? ?现代操作系统使用虚拟内存来管理物理RAM资源。应用程序看到并使用虚拟地址空间而非直接操控物理地址；操作系统和CPU通过页表将虚拟地址转换为实际物理地址。

7. 缓冲与Caching:?
? ?为了提高效率, CPU 可能会利用快速但容量较小的缓冲(比如 L1, L2 或者 L3 缓存) 来暂时保持近期访问过得数据.

8. 二进制表示法:?
? ?所有类型数据最终都以二进制形式存在于 RAM 中; 比如数字通过各类数码(binary code), 字符串通过字符集编码(比如 ASCII 或 UTF-8).

9. 逻辑结构:?
? ? 高级语言往往支持复杂类型(比如对象, 结构体等), 这些复杂类型背后也会被转化成基本单元组合起来并按照上述原则进行布局.

总之，在现代计算机架构下，数据以非常精确和有效率地方式被组织、管理并储存在 RAM 中供 CPU 访问执行指令。

整数在内存中的存储

在计算机内存中，整数通常以二进制形式存储。不同的编程语言和操作系统可能会有不同的表示方式，但大多数情况下遵循以下几种标准：

1. 定长表示：整数一般用固定长度的位(bit)来表示，常见的长度有8位、16位、32位和64位等。

2. 无符号与有符号：
? ?- 无符号整数（Unsigned Integers）只能表示非负值，其所有位都用于存储实际数字。
? ?- 有符号整数（Signed Integers）可以表示正负值，通常最高位被用作符号位（sign bit），0代表正数或零，1代表负数。剩余的部分则用于存储实际数字。

3. 补码表示法：对于有符号整数而言，在现代计算机系统中普遍采用补码（Two's Complement）来处理负值。这种方法允许加法运算统一处理正负值，并且解决了原码和反码存在+0和-0两个零点问题。

4. 字节序/端序(Byte Order/Endianness)：
? ?- 大端模式(Big-endian)：较高有效字节(high-order byte)放在低地址处。
? ?- 小端模式(Little-endian)：较低有效字节(low-order byte)放在低地址处。

5. 对齐(Alignment): 整型数据经常按照它们自身大小进行对齐。例如, 一个32-bit 的整型可能会被要求放置在一个地址是4倍数上。

假设我们使用32-bit系统并考虑一个带符号的32-bit整型变量int x = -123; 在内存中如何存储：

• 首先将123转换为二进制得到 00000000 00000000 00000000 01111011
• 然后取反得到 11111111 11111111 11111111 10000100
• 最后加1得到补码 11111111 11111111 11111111 10000101
• 如果是小端模式，则这些字节从左至右依次写入更高地址；如果是大端模式，则顺序相反。

浮点数在内存中的存储

浮点数在计算机内存中的存储遵循IEEE 754标准，这是一个国际标准，用于确保不同计算机系统之间能够一致地表示和处理浮点数。根据这个标准，浮点数分为几种不同的格式，其中最常见的有单精度（32位）和双精度（64位）。

以单精度浮点数为例，其由三部分组成：
1. 符号位（Sign bit）：1位
2. 指数部分（Exponent）：8位
3. 尾数或有效数字部分（Mantissa）：23位

具体结构如下：

S EEEEEEEE FFFFFFFFFFFFFFFFFFFFFFF
| ? ?| ? ? ? ? ? ? ? |
| ? ?| ? ? ? ? ? ? ? +-- 尾数部分 (23 bits)
| ? ?+-- 指数部分 (8 bits)
+-- 符号位 (1 bit)

- 符号位决定了数字的正负。0代表正值，1代表负值。
- 指数用来表示数字的范围或者大小级别。它使用“偏移量”编码方式，在单精度中偏移量是127。实际指数等于存储指数值减去127。
- 尾数包含了该数字除去整个小数点前面那个非零数字后剩余的所有有效数字。例如对于十进制中的1234.56,如果我们只写出234.56，则省略掉了第一个非零整数；类似地，在二进制下也会省略掉第一个非零比特。

举例说明：

考虑将十进制中的5.75转换为IEEE 754格式下的32-bit单精度浮点表示方法：

• 首先将5.75转换为二进制形式得到101.11。
• 然后找到二进制科学记法形式即 ( 1.0111 \times 2^2 )。
• 接着确定各个字段：
• 因为是正值所以符号位置0；
• 指数字段需要加上偏移量127: ( 2 + 127 = 129 )，而129在二进制下是10000001；
• 将尾数组成23比特长度(若不足则补0): (01110000000000000000000)。

因此5.75在内存里面按照IEEE754标准被编码成如下32比特序列:

0 ? | ? 10000001 ? | ? 01110000000000000000000
(符号)| ? ? (指针) ? ? ? | ? ? ? ? ?(尾数组成)
?

对于双精度格式（64-bit），结构类似但每一部份都更长：
- 符号仍旧占用1bit，
- 指针扩展至11bits，
- 尚余52bits给予尾示意义上更多细节与范围广阔性之尺寸数据段落(Mantissa)使用。

总体来说，IEEE754规范使得浮点运算可以跨平台进行，并且提供了相当程度上稳定可靠之结果输出保证。
?

好啦！介绍完了整数和浮点数在内存中的存储，让我们来看一个神奇的小栗子ovo

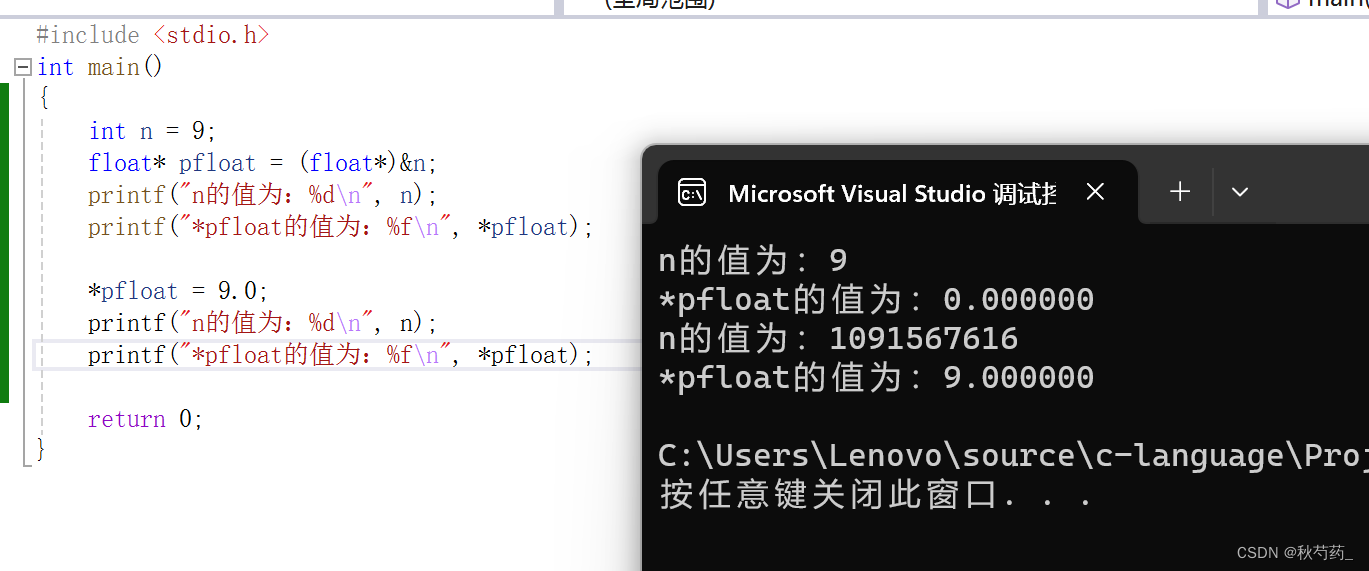
q1:为什么9还原成浮点数，就成了0.000000？

9以整数的形式存储在内存中，得到如下二进制序列：

0000 0000 0000 0000 0000 0000 0000 1001

然后，将9的二进制序列按照浮点数的形式拆分，第一位符号位s=0，后面八位指数E=00000000

最后23位有效数字为M=000 0000 0000 0000 0000 1001

由于指数E全为0，所以

V=（-1)^0 ? 0.00000000000000000001001 ? 2^(-126)

显然V是一个很小的数字

q2：浮点数9.0，以整数的形式打印出来为什么是1091567616？

浮点数9.0相当于二进制的1001.0，科学计数法形式就是1.001 ? 2^3 ,9.0=(-1)^0 * 1.001 *2^3

所以第一位符号位是S，E=3+127=130，M等于001后面加上20个0

二进制形式就是 0 10000010 001 0000 0000 0000 0000 0000

当这个32位二进制数，被当作整数来拆解时就是整数在内存中的补码，原码是1091567616

本篇文章到此就结束啦，创作不易，给博主点个赞吧！！