循环神经网络

一、序列模型

1、解决问题：

对于事件有关的序列数据，通过使用历史观测来预测下一个未来观测。

2、自回归模型

第一种策略：可能不需要相当长的序列，只需要满足某个长度为的时间跨度。模型即自回归模型（autoregressive models）。

第二种策略：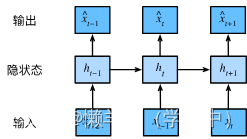

保留一些对过去观测的总结，同时更新预测和总结。模型基于，以及公式更新的模型。由于从未被观测到，故该类模型称为隐变量自回归模型（latent autoregressive models）

3、马尔可夫模型

可以理解为自回归模型的第一种策略

例如：一阶马尔可夫模型即为1表示为：

二、文本预处理

主要流程有以下几个步骤：

2.1 词元化（tokenize）

将文本列表转化为词元（token）列表，这里的词元一般为一个字符串。中文词元一般为一个字或者一个词。

2.2 获取语料（corpus）

将词元列表统计每个唯一词元的出现频率，为该词元分配一个数字索引，并按频率高低排序得到词元和频率的键值对列表。同时，为了将来数据的处理方便，使用词元的索引作为corpus中的“键”。

三、语言模型

3.1?语言模型估计文本序列的联合概率

利用马尔可夫模型，涉及一个、两个和三个变量的概率公式分别被称为?一元语法（unigram）、二元语法（bigram）和三元语法（trigram）模型。使用统计方法时常采用n元语法（长为n的词元序列）。

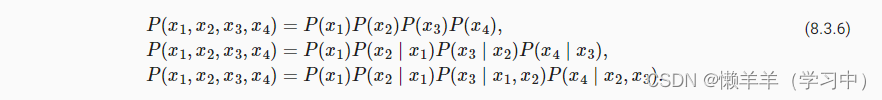
3.2??拉普拉斯平滑

使用统计词元x在整个文本中的出现次数，表示连续单词对的出现次数，

计算为任何以单词x开头的句子的概率,为了防止出现除以0的情况，通常在所有计数添加一个小常量。

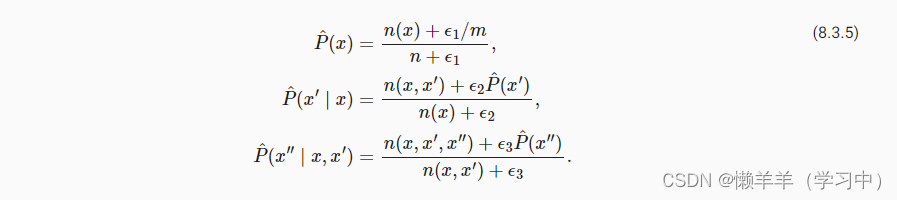
四、循环神经网络

4.1 隐变量模型

? ? ? ? 其中是隐状态，也称为隐藏变量，存储到时间步t-1的序列信息。

循环层:

输出层：

4.2 困惑度（Perplexity)

公式：

困惑度的最好的理解是“下一个词元的实际选择数的调和平均数”，也可直观理解为当我们给定一段非常标准的，高质量的，符合人类自然语言习惯的文档作为测试集时，模型生成这段文本的概率越高，就认为模型的困惑度越小，模型也就越好。

五、现代循环神经网络

5.1 门控循环单元（GRU）

1.问题背景

考虑到早期观测值对预测所有未来观测值具有重要意义，或者一些词元没有相关的观测值，以及序列的各个部分存在逻辑中断的情况，通过使用门控单元来控制信息的流动。这些门控单元允许网络选择性地从输入中选择性地忽略一些信息，或者从过去的状态中选择性地记忆一些信息。这样就可以更好地捕捉时间序列数据中的长期依赖关系，从而提高模型的性能。

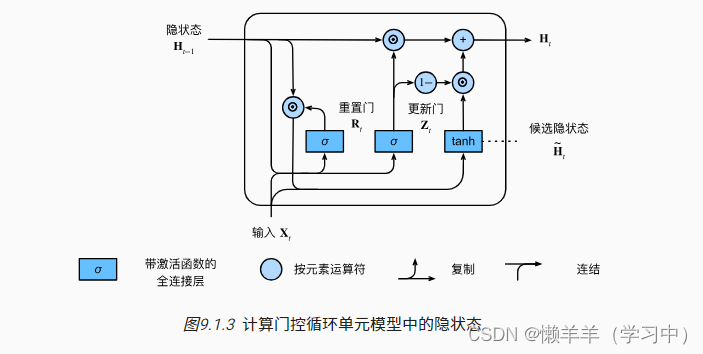
2.门控隐状态

• 重置门和更新门

? ? ? ? 重置门控制"可能还想记住“的过去状态的数量；更新门控制新状态有多少个是旧状态的副本。

• 候选隐状态

将重置门与常规隐状态更新机制集成，得到在时间步t的候选隐状态。

和 的元素相乘可以减少以往状态的影响。 每当重置门中的项接近1时， 我们恢复普通的循环神经网络。 对于重置门中所有接近0的项， 候选隐状态是以作为输入的多层感知机的结果。 因此，任何预先存在的隐状态都会被重置为默认值。

• 隐状态

将上述候选隐状态结合更新门的效果，进一步确定新的隐状态在多大程度上来自旧的状态和新的候选状态。更新门仅需要在和之间进行按元素的凸组合就可以实现这个目标。 这就得出了门控循环单元的最终更新公式：

当更新门接近1时，模型就倾向只保留旧状态。这些设计可以帮助我们处理循环神经网络中的梯度消失问题， 并更好地捕获时间步距离很长的序列的依赖关系。 例如，如果整个子序列的所有时间步的更新门都接近于1， 则无论序列的长度如何，在序列起始时间步的旧隐状态都将很容易保留并传递到序列结束。

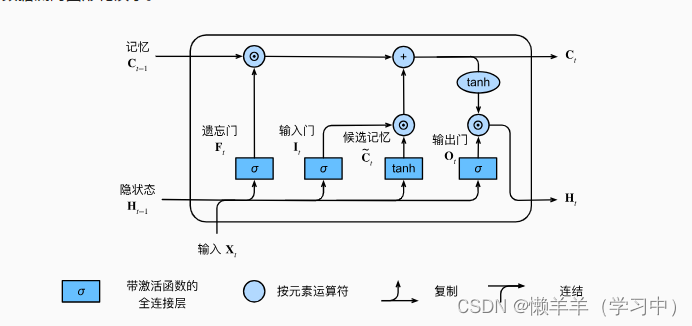
5.2 长短期记忆网络（LSTM）

LSTM的关键是细胞状态，细胞状态类似于传送带，细胞的状态在整个链上运行，只有一些小的线性操作作用其上，信息很容易保持不变的流过整个链。

1.门控记忆元

• 候选记忆元
• 输入门、忘记门和输出门

? ? ? ? 输入门：决定在细胞状态中存储什么信息，在LSTM机制中控制采用多少来自候选记忆元的新数据。

? ? ? ? 忘记门：决定从细胞状态中丢弃什么信息，在LSTM机制中控制保留多少过去的记忆元的内容，

? ? ? ? 输出门：决定要输出什么。 此输出将基于细胞状态

• 记忆元：控制输入和遗忘
• 隐状态：
• 

????????