力扣120. 三角形最小路径和(Java 动态规划)
Problem: 120. 三角形最小路径和
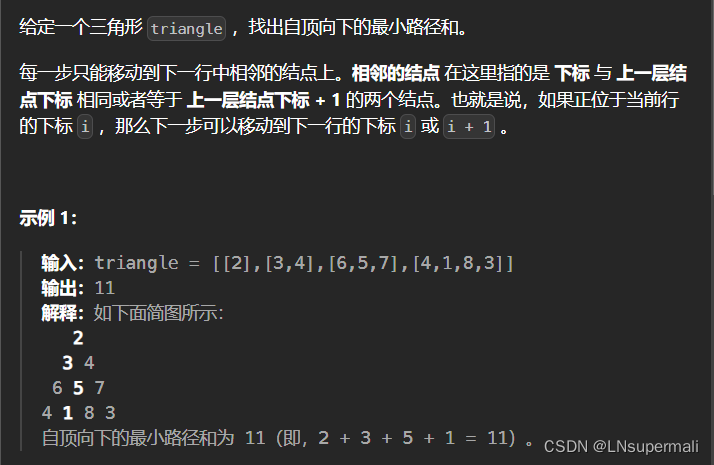
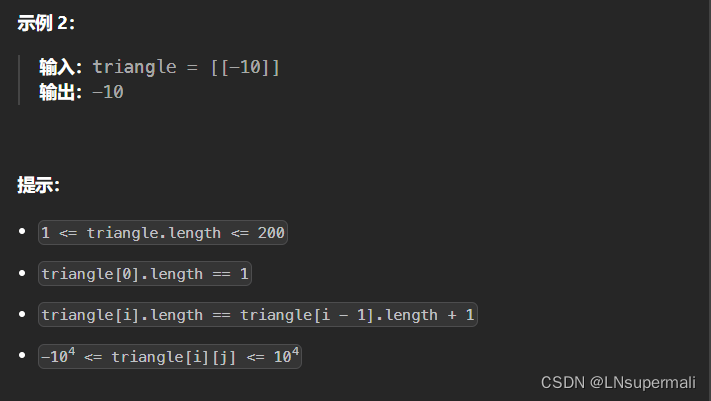
题目描述
思路
Problem:64. 最小路径和
本题目可以看作是在上述题目的基础上改编而来,具体的思路:
1.记录一个int类型的大小的 n 乘 n n乘n n乘n的数组(其中 n n n为数组triangle的行数)用于记录每一个当前阶段的最小路径和
2.大体上可以依据题意得出动态转移方程为dp[i][j] = Math.min(dp[i - 1][j - 1], dp[i - 1][j]) + triangle.get(i).get(j);(其中i与j为遍历数组时的下标)即当前位置的最小路径和为其相邻左侧位置和左上方位置中的最小值加上数组triangle当前位置的值;
3.我们需要单独处理dp数组的第一列和dp主对角线位置的值(由于dp可以看作为一个方阵,主对角线即为下标(i,i)位置的值):第一列依次向下累加;主对角线位置沿主对角线向下累加
3.我们仔细思考便可注意到,由于我们需要对主对角线的元素做一个单独的处理,而该处理会使得dp数组中最后一个位置不一定是最小路径和!!!(我们很容易想到,由于本题目是在求取三角形最小路径和因为我们在单独处理主对角线时不是由其相邻的正上方与正左侧共同得出所以在往下的动态转移过程中就不能确保当前位置就是当前整个决策阶段的最小值,但是我们可以得出对于整个阶段的最小值是存在于dp数组的最后一行的)所以我们求出dp数组中最后一行的最小值,即为给定三角形的最小路径和
解题方法
1.得出数组triangle的大小int n = triangle.size();;并定义int数组dp大小为 n 行 n 列 n行n列 n行n列
2.初始化dp数组第1行第1列位置(索引下标为(0,0))的值dp[0][0] = triangle.get(0).get(0);
3.从dp数组第二行开始执行动态转移方程,同时处理第一列和dp主对角线位置的值
4.求取dp数组最后一行的最小值并返回。
复杂度
时间复杂度:
O ( N × N ) O(N\times N) O(N×N)其中 N N N为数组triangle的大小
空间复杂度:
O ( N × N ) O(N\times N) O(N×N)
Code
class Solution {
/**
* The minimum path sum of triangles is obtained by dynamic programming
* @param triangle Given martix
* @return int
*/
public int minimumTotal(List<List<Integer>> triangle) {
int n = triangle.size();
//Record the sum of the shortest paths
int[][] dp = new int[n][n];
dp[0][0] = triangle.get(0).get(0);
for (int i = 1; i < n; ++i) {
//Handle the Column 0
dp[i][0] = dp[i - 1][0] + triangle.get(i).get(0);
for (int j = 1; j < i; ++j) {
dp[i][j] = Math.min(dp[i - 1][j - 1], dp[i - 1][j]) + triangle.get(i).get(j);
}
//Dispose of (i, i)
dp[i][i] = dp[i - 1][i - 1] + triangle.get(i).get(i);
}
int min = Integer.MAX_VALUE;
for (int i = 0; i < n; ++i) {
if (dp[n - 1][i] < min) {
min = dp[n - 1][i];
}
}
return min;
}
}
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!