前缀和——OJ题（二）

📘北尘_：个人主页
🌎个人专栏:《Linux操作系统》《经典算法试题 》《C++》 《数据结构与算法》

??走在路上，不忘来时的初心

---

一、和为 k 的子数组

1、题目讲解

2、思路讲解

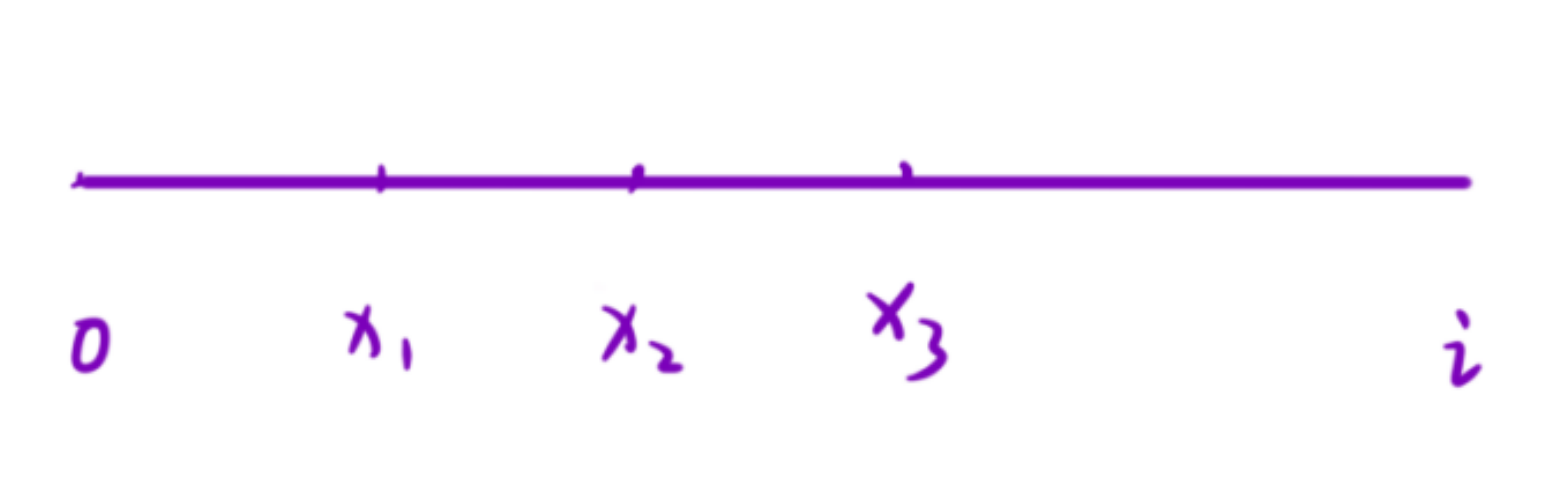
设 i 为数组中的任意位置，? sum[i] 表? [0, i] 区间内所有元素的和。
想知道有多少个「以 i 为结尾的和为 k 的?数组」，就要找到有多少个起始位置为 x1, x2, x3… 使得 [x, i] 区间内的所有元素的和为 k 。那么 [0, x] 区间内的和是不是就是sum[i] - k 了。于是问题就变成：
? 找到在 [0, i - 1] 区间内，有多少前缀和等于 sum[i] - k 的即可。
我们不?真的初始化?个前缀和数组，因为我们只关?在 i 位置之前，有多少个前缀和等于sum[i] - k 。因此，我们仅需??个哈希表，?边求当前位置的前缀和，?边存下之前每?种前缀和出现的次数。

3、代码实现

class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
        unordered_map<int,int> hash;
        hash[0]=1;

        int sum=0,ret=0;
        for(auto x:nums)
        {
            sum+=x;  
            if(hash.count(sum-k)) ret+=hash[sum-k];
            hash[sum]++;  
        }
        return ret;
    }
};

---

二、和可被 K 整除的?数组

1、题目讲解

2、思路讲解

? 同余定理
如果 (a - b) % n == 0 ，那么我们可以得到?个结论： a % n == b % n 。??字叙述就是，如果两个数相减的差能被 n 整除，那么这两个数对 n 取模的结果相同。
例如： (26 - 2) % 12 == 0 ，那么 26 % 12 == 2 % 12 == 2 。
? c++ 中负数取模的结果，以及如何修正「负数取模」的结果
a. c++ 中关于负数的取模运算，结果是「把负数当成正数，取模之后的结果加上?个负号。
例如： -1 % 3 = -(1 % 3) = -1
b. 因为有负数，为了防?发?「出现负数」的结果，以 (a % n + n) % n 的形式输出保证为正。
例如： -1 % 3 = (-1 % 3 + 3) % 3 = 2

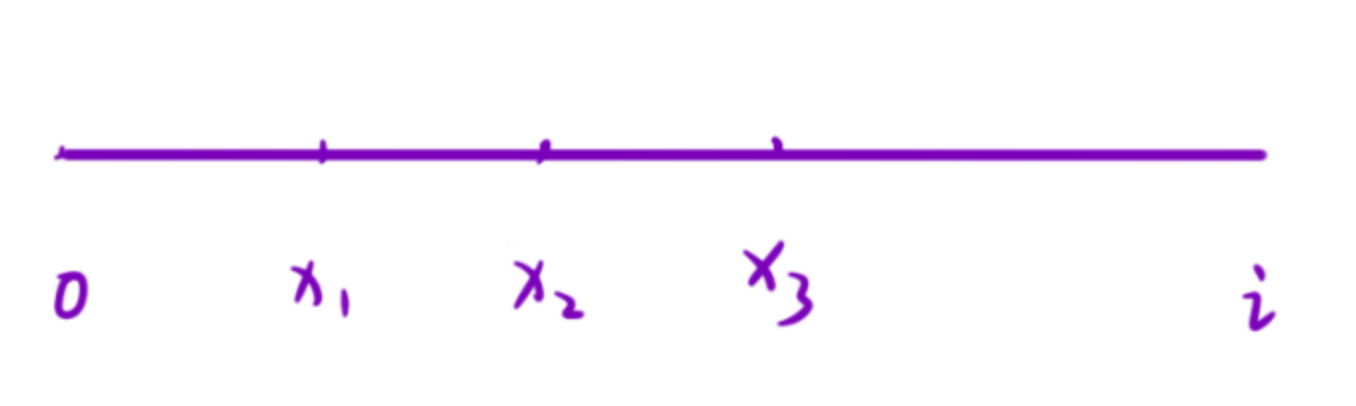
设 i 为数组中的任意位置，? sum[i] 表? [0, i] 区间内所有元素的和。
? 想知道有多少个「以 i 为结尾的可被 k 整除的?数组」，就要找到有多少个起始位置为 x1, x2, x3… 使得 [x, i] 区间内的所有元素的和可被 k 整除。
? 设 [0, x - 1] 区间内所有元素之和等于 a ， [0, i] 区间内所有元素的和等于 b ，可得(b - a) % k == 0 。
? 由同余定理可得， [0, x - 1] 区间与 [0, i] 区间内的前缀和同余。于是问题就变成：
? 找到在 [0, i - 1] 区间内，有多少前缀和的余数等于 sum[i] % k 的即可。
我们不?真的初始化?个前缀和数组，因为我们只关?在 i 位置之前，有多少个前缀和等于sum[i] - k 。因此，我们仅需??个哈希表，?边求当前位置的前缀和，?边存下之前每?种前缀和出现的次数。

3、代码实现

class Solution {
public:
    int subarraysDivByK(vector<int>& nums, int k) {
        unordered_map<int,int> hash;
        hash[0]=1;

        int sum=0,ret=0;
        for(auto x:nums)
        {
            sum+=x;
            int r=(sum%k+k)%k;
            if(hash.count(r)) ret+=hash[r];
            hash[r]++;
        }
        return ret;
    }
};

---

三、连续数组

1、题目讲解

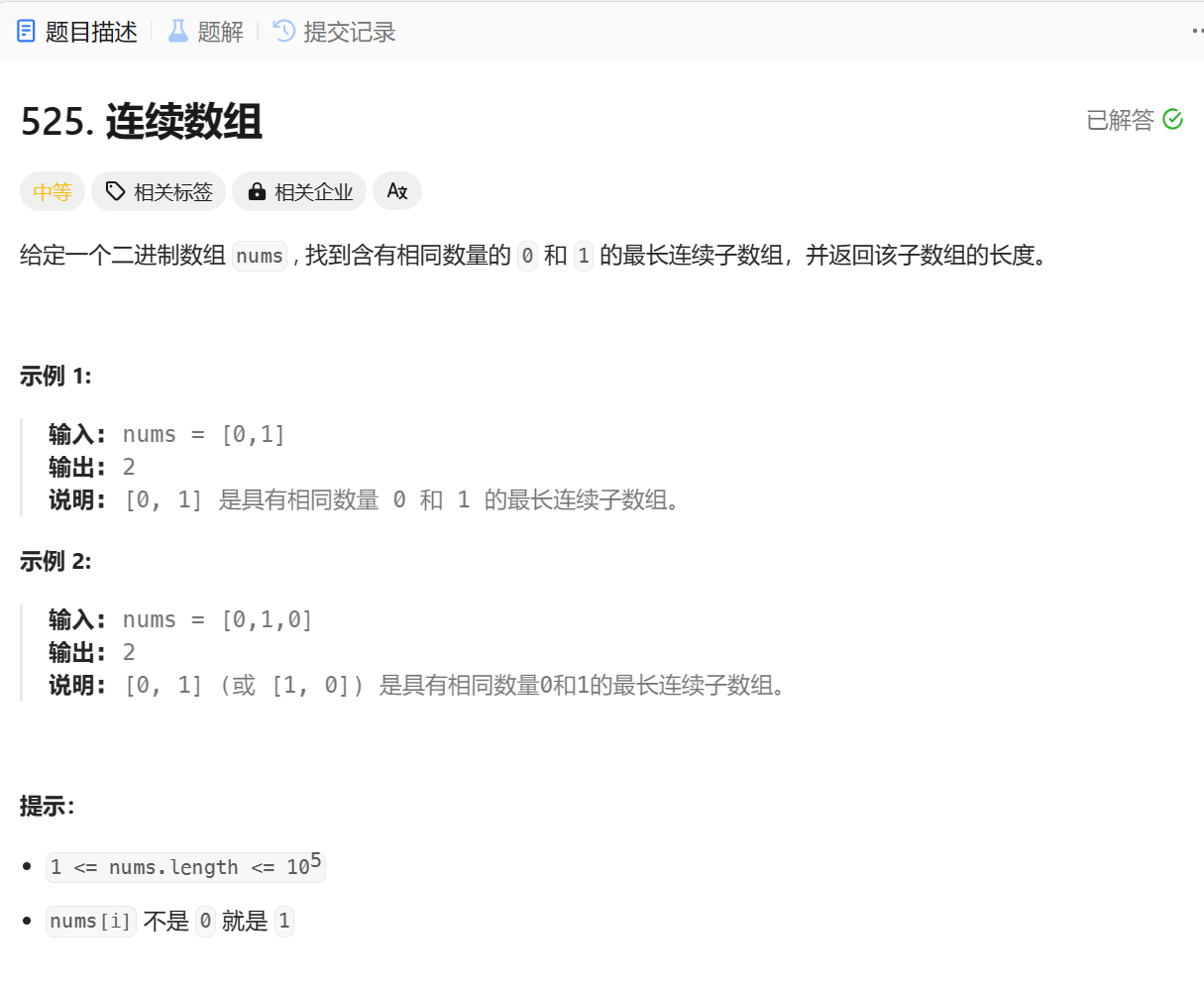
2、思路讲解

稍微转化?下题?，就会变成我们熟悉的题：
? 本题让我们找出?段连续的区间， 0 和 1 出现的次数相同。
? 如果将 0 记为 -1 ， 1 记为 1 ，问题就变成了找出?段区间，这段区间的和等于 0 。
? 于是，就和 560. 和为 K 的?数组 这道题的思路?样

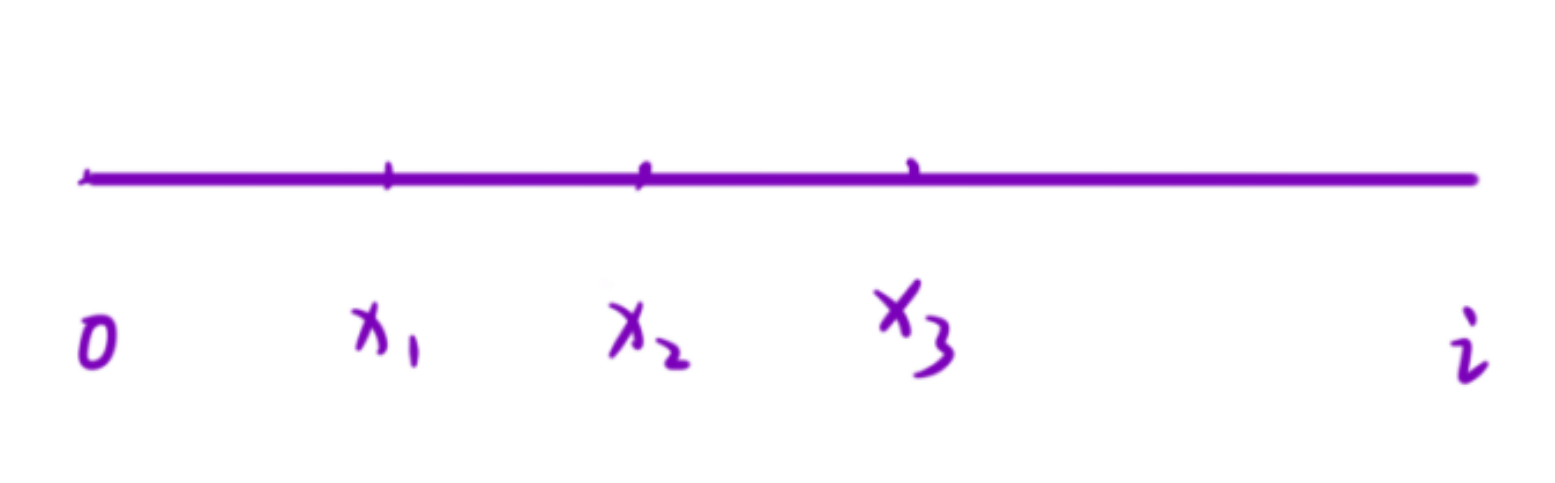
设 i 为数组中的任意位置，? sum[i] 表? [0, i] 区间内所有元素的和。
想知道最?的「以 i 为结尾的和为 0 的?数组」，就要找到从左往右第?个 x1 使得 [x1, i]区间内的所有元素的和为 0 。那么 [0, x1 - 1] 区间内的和是不是就是 sum[i] 了。于是问题就变成：
? 找到在 [0, i - 1] 区间内，第?次出现 sum[i] 的位置即可。
我们不?真的初始化?个前缀和数组，因为我们只关?在 i 位置之前，第?个前缀和等于 sum[i]的位置。因此，我们仅需??个哈希表，?边求当前位置的前缀和，?边记录第?次出现该前缀和的位置。

3、代码实现

class Solution {
public:
    int findMaxLength(vector<int>& nums) {
        unordered_map<int,int> hash;
        hash[0]=-1;
        int sum=0,ret=0;
        for(int i=0;i<nums.size();i++)
        {
            sum+=(nums[i]==0?-1:1);
            if(hash.count(sum)) ret=max(ret,i-hash[sum]);
            else hash[sum]=i;
        }
        return ret;
    }
};

---

四、矩阵区域和

1、题目讲解

2、思路讲解

?维前缀和的简单应?题，关键就是我们在填写结果矩阵的时候，要找到原矩阵对应区域的「左上?」以及「右下?」的坐标（推荐?家画图）
左上?坐标： x1 = i - k，y1 = j - k ，但是由于会「超过矩阵」的范围，因此需要对 0 取?个 max 。因此修正后的坐标为： x1 = max(0, i - k), y1 = max(0, j - k) ;
右下?坐标： x1 = i + k，y1 = j + k ，但是由于会「超过矩阵」的范围，因此需要对 m - 1 ，以及 n - 1 取?个 min 。因此修正后的坐标为： x2 = min(m - 1, i + k), y2 = min(n - 1, j + k) 。
然后将求出来的坐标代?到「?维前缀和矩阵」的计算公式上即可~（但是要注意下标的映射关系）

3、代码实现

class Solution {
public:
    vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int k) {
        int m = mat.size(), n = mat[0].size();
        vector<vector<int>> dp(m + 1, vector<int>(n + 1));
        // 1. 预处理前缀和矩阵
        for(int i = 1; i <= m; i++)
        for(int j = 1; j <= n; j++)
        dp[i][j] = dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1] + mat[i - 1][j - 1];
        
        // 2. 使?
        vector<vector<int>> ret(m, vector<int>(n));
        for(int i = 0; i < m; i++)
        for(int j = 0; j < n; j++)
        {
        int x1 = max(0, i - k) + 1, y1 = max(0, j - k) + 1;
        int x2 = min(m - 1, i + k) + 1, y2 = min(n - 1, j + k) + 1;
        ret[i][j] = dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] +dp[x1 - 1][y1 - 1];
        }
        return ret;  
    }
};

---