LeetCode(33) 搜索旋转排序数组
发布时间:2024年01月04日

整数数组?nums?按升序排列,数组中的值?互不相同?。
在传递给函数之前,nums?在预先未知的某个下标?k(0 <= k < nums.length)上进行了?旋转,使数组变为?[nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]](下标?从 0 开始?计数)。例如,?[0,1,2,4,5,6,7]?在下标?3?处经旋转后可能变为?[4,5,6,7,0,1,2]?。
给你?旋转后?的数组?nums?和一个整数?target?,如果?nums?中存在这个目标值?target?,则返回它的下标,否则返回?-1?。
你必须设计一个时间复杂度为?O(log n)?的算法解决此问题。
示例 1:
输入:nums = [4,5,6,7,0,1,2], target = 0 输出:4
示例?2:
输入:nums = [4,5,6,7,0,1,2], target = 3 输出:-1
示例 3:
输入:nums = [1], target = 0 输出:-1
提示:
1 <= nums.length <= 5000-104 <= nums[i] <= 104nums?中的每个值都?独一无二- 题目数据保证?
nums?在预先未知的某个下标上进行了旋转 -104 <= target <= 104
?思路:看到规定时间复杂度肯定是二分查找 在二分查找上有一点点改动,首先你最开始分的时候会把数列分成两部分,有一个部分肯定有序。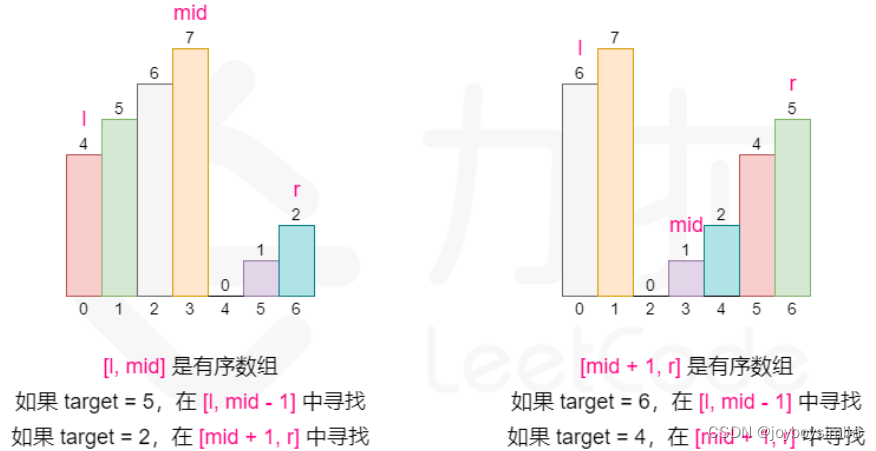
class Solution {
public int search(int[] nums, int target) {
int n = nums.length;
if (n == 0) {
return -1;
}
if (n == 1) {
return nums[0] == target ? 0 : -1;
}
int l = 0, r = n - 1;
while (l <= r) {
int mid = (l + r) / 2; // 以mid分成2个部分
if (nums[mid] == target) {
return mid;
}
if (nums[0] <= nums[mid]) { // 左边部分有序
if (nums[0] <= target && target < nums[mid]) {
r = mid - 1;
} else {
l = mid + 1;
}
} else { // 右边有序
if (nums[mid] < target && target <= nums[n - 1]) {
l = mid + 1;
} else {
r = mid - 1;
}
}
}
return -1;
}
}
文章来源:https://blog.csdn.net/m0_48590589/article/details/135385588
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 【论文阅读】Video-to-Video Synthesis
- LLM之RAG理论(一)| CoN:腾讯提出笔记链(CHAIN-OF-NOTE)来提高检索增强模型(RAG)的透明度
- <C++>STL->list
- kafka发送大消息
- MSE Nacos:解决敏感配置的安全隐患
- Spark原理——运行过程
- 大模型:我也会自监督学习~
- 深度学习(4)--Keras安装
- 设计模式(4)--类行为(3)--解释器
- Flink运行架构以及容错机制