leetcode - 1026. Maximum Difference Between Node and Ancestor
Description
Given the root of a binary tree, find the maximum value v for which there exist different nodes a and b where v = |a.val - b.val| and a is an ancestor of b.
A node a is an ancestor of b if either: any child of a is equal to b or any child of a is an ancestor of b.
Example 1:

Input: root = [8,3,10,1,6,null,14,null,null,4,7,13]
Output: 7
Explanation: We have various ancestor-node differences, some of which are given below :
|8 - 3| = 5
|3 - 7| = 4
|8 - 1| = 7
|10 - 13| = 3
Among all possible differences, the maximum value of 7 is obtained by |8 - 1| = 7.
Example 2:
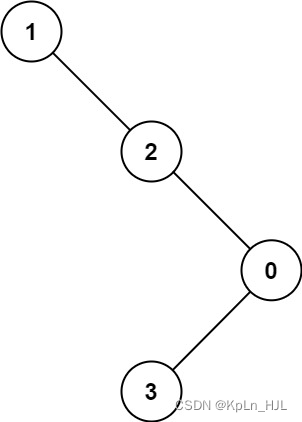
Input: root = [1,null,2,null,0,3]
Output: 3
Constraints:
The number of nodes in the tree is in the range [2, 5000].
0 <= Node.val <= 10^5
Solution
Solved after hints.
For each node, find the smallest and largest value of its descendants, and the result will be either node.val - smallest or largest - node.val.
Go with postorder traversal, and use a map to store the values of the nodes.
Time complexity:
o
(
n
)
o(n)
o(n)
Space complexity:
o
(
n
)
o(n)
o(n)
Code
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def maxAncestorDiff(self, root: Optional[TreeNode]) -> int:
nodes_info = {None: [100001, -1]}
stack = [(root, 0)]
res = 0
while stack:
node, status = stack.pop()
if status == 0:
stack.append((node, 1))
if node.right:
stack.append((node.right, 0))
if node.left:
stack.append((node.left, 0))
else:
left_min, left_max = nodes_info[node.left]
right_min, right_max = nodes_info[node.right]
nodes_info[node] = [min(left_min, right_min, node.val), max(left_max, right_max, node.val)]
res = max(res, max([nodes_info[node][1] - node.val, node.val - nodes_info[node][0]]))
return res
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- CHAPTER 13:《DESIGN A SEARCH AUTOCOMPLETE SYSTEM》 第13章 《设计搜索自动补全系统》
- Java 基础学习(十一)File类与I/O操作
- leetcode刷题(剑指offer) 287.寻找重复数
- 【linux提权】利用setuid进行简单提权
- 中国化妆品头部企业环亚集团携美肤宝、法兰琳卡、滋源、肌肤未来等“新朋友”加入实在智能数智生态圈
- FreeRTOS学习--59讲 Tickless低功耗
- Elasticsearch8 创建新用户PUT请求方式
- 【小沐学Python】Python实现语音识别(vosk)
- 基于Java (spring-boot)的宠物管理系统
- 淘宝商品详情数据接口指南(taobao.item_get)