数据结构第十三弹---链式二叉树基本操作(上)

1、结构定义

实现一个数据结构少不了数据的定义，所以第一步需要定义二叉树的机构。

typedef char BTDataType;//定义数据类型，可以根据需要更改

typedef struct BinaryTreeNode
{
	struct BinaryTreeNode* left;//左指针
	struct BinaryTreeNode* right;//右指针
	BTDataType data;//存储数据
}BTNode;

2、手动创建二叉树

初次学习链式二叉树，对于创建一个二叉树较难理解，所以先手动创建二叉树，学习一些操作之后再来通过函数实现链式二叉树。

//创建结点函数
BTNode* BuyTree(BTDataType x)
{
	BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
	newnode->data = x;
	newnode->left = NULL;
	newnode->right = NULL;

	return newnode;
}
//创建结点

	BTNode* A = BuyTree('A');
	BTNode* B = BuyTree('B');
	BTNode* C = BuyTree('C');
	BTNode* D = BuyTree('D');
	BTNode* E = BuyTree('E');
	BTNode* F = BuyTree('F');
//链接结点
	A->left = B;
	A->right = E;
	B->left = C;
	B->right = D;
	E->left = F;

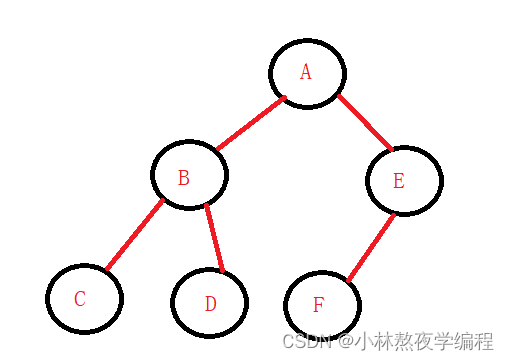
3、前序遍历

前序遍历，又称先根遍历。
遍历顺序：根，左子树，右子树。

代码实现

void PrevOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	printf("%c ", root->data);//根
	PrevOrder(root->left);//左子树
	PrevOrder(root->right);//右子树
}

此处实现的遍历版本是将空指针也打印出来的版本，更适合新手理解
测试

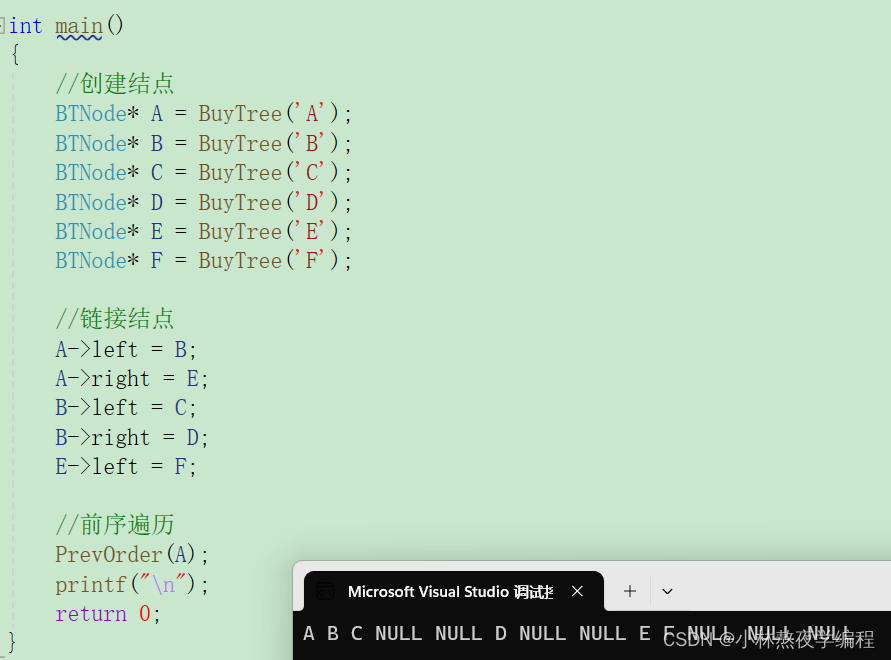
4、中序遍历

中序遍历，又称中根遍历。
遍历顺序：左子树，根，右子树。

代码实现

void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	InOrder(root->left);//左子树
	printf("%c ", root->data);//根
	InOrder(root->right);//右子树
}

测试

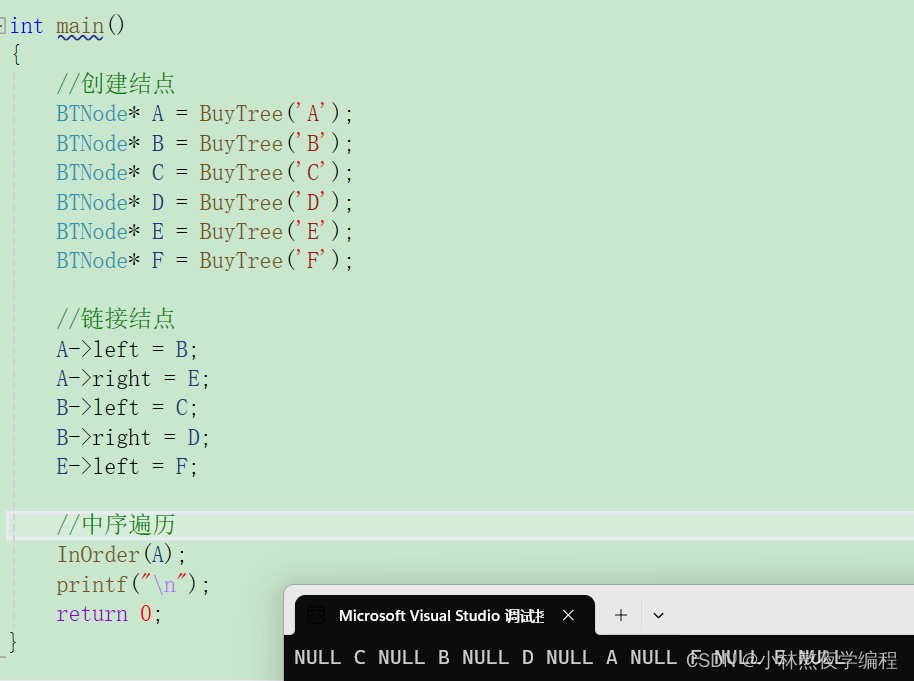
5、后序遍历

后序遍历，又称后根遍历。
遍历顺序：左子树，右子树，根。

代码实现

void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	PostOrder(root->left);//左子树
	PostOrder(root->right);//右子树
	printf("%c ", root->data);//根
}

测试

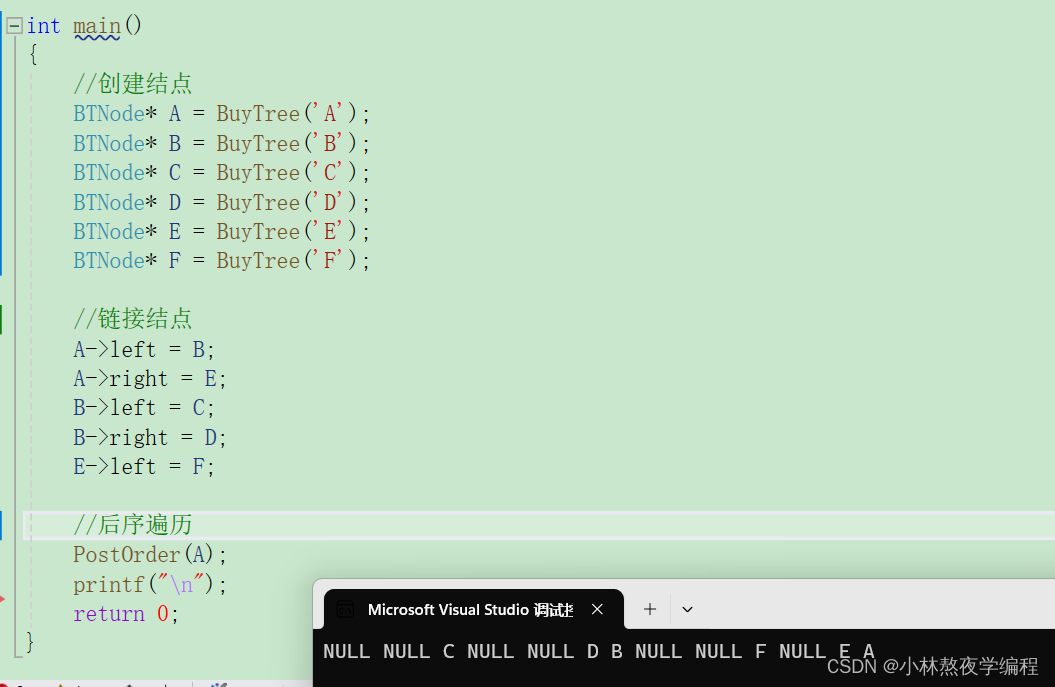
6、层序遍历

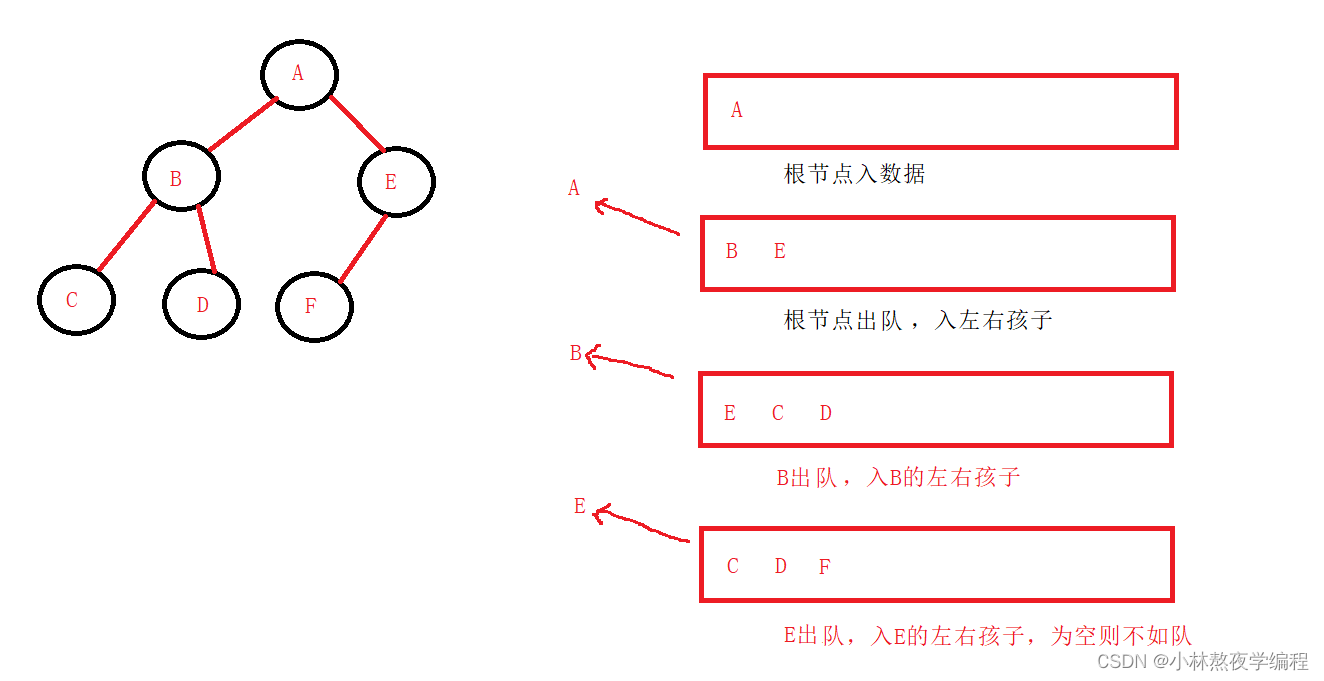
层序遍历，自上到下，自左到右依次访问数的结点就是层序遍历。

思想（借助一个队列）：
1、先将根节点入队，然后开始从队头出数据
2、出队头的数据同时将队头左右子树的结点入队（遇到NULL则不入队）
3、重复第二步，直到队列为空

代码实现

void LevelOrder(BTNode* root)
{
	Queue q;//创建爱你队列
	QueueInit(&q);//初始化队列
	if (root)//根节点不为空则入队
		QueuePush(&q, root);
	while (!QueueEmpty(&q))//队列不为空，循环继续
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);//出队
		printf("%c ", front->data);//打印数据

		if (front->left)//如果左子树不为空则入队
			QueuePush(&q, front->left);
		if (front->right)//右子树不为空入队
			QueuePush(&q, front->right);
	}

	QueueDestory(&q);//销毁队列
}

测试

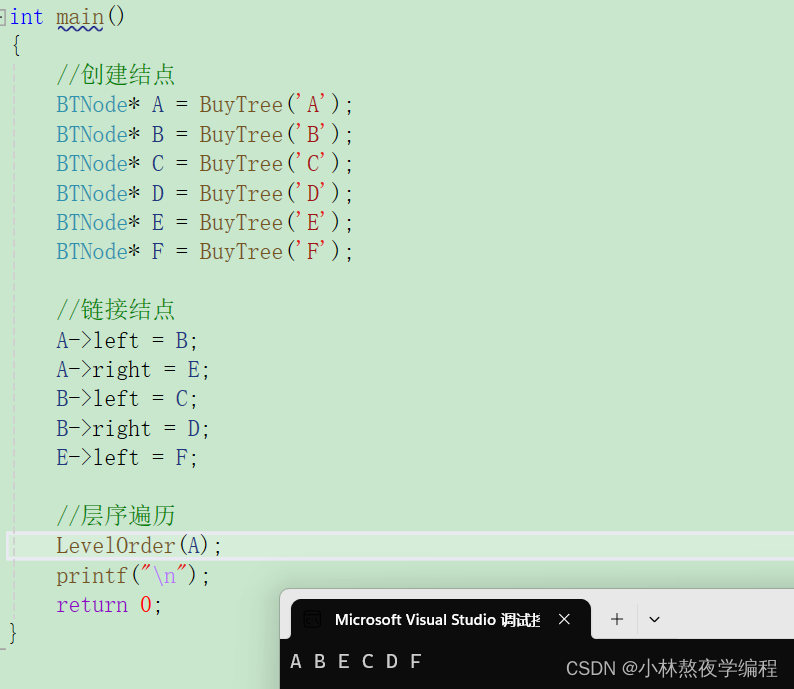
7、计算结点个数

计算结点个数时，可以将问题拆成子问题
1、为空时，结点个数为0
2、不为空时，结点个数=左子树结点个数+右子树结点个数+1(根节点)

代码实现

int TreeSize(BTNode* root)
{
	return root==NULL?0:TreeSize(root->left) + TreeSize(root->right) + 1;
}

测试

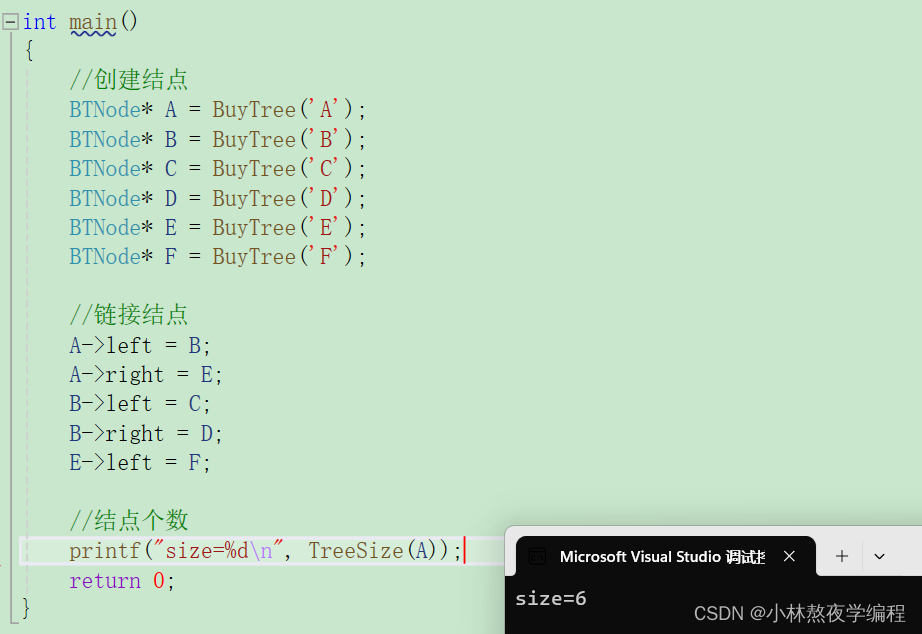
8、计算叶子结点个数

计算叶子结点个数时，可以将问题拆成子问题
1、为空时，叶子结点个数为0
2、结点左右孩子为空时，叶子结点个数为1
3、结点不为空，叶子结点个数=左子树叶子结点个数+右子树叶子结点个数

代码实现

int TreeLeafSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	if (root->left == NULL && root->right==NULL)
	{
		return 1;
	}
	return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}

测试

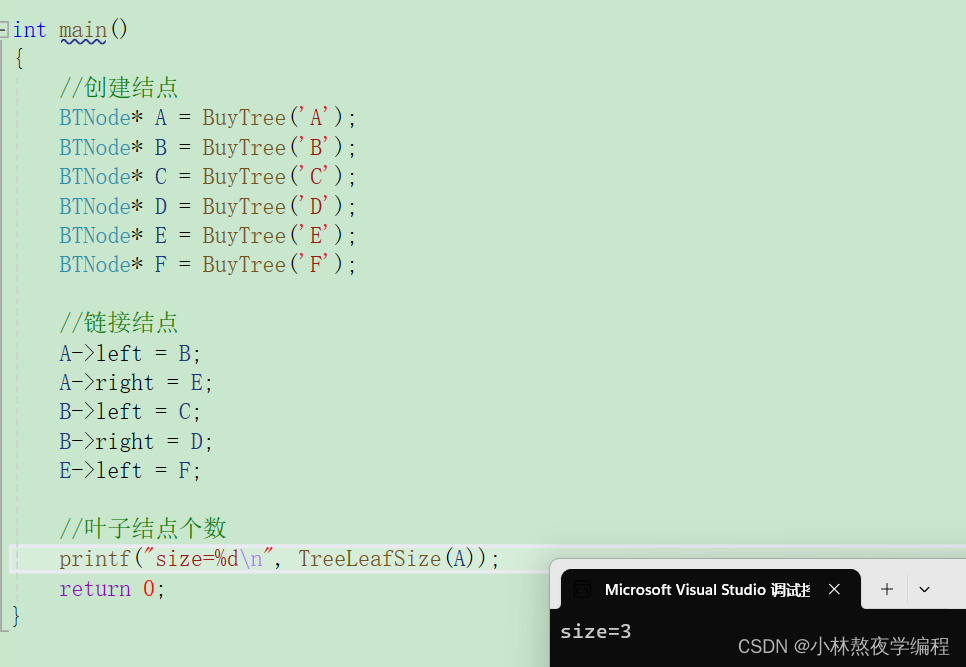
9、计算第K层结点个数

计算第K层结点个数时，可以将问题拆分成子问题。
1、为空和非法时，结点个数为0个
2、为第一层时，结点个数为1个
3、不为空且合法时，第K层的结点个数=第K-1层的左子树结点个数+第K-1层的右子树结点个数

代码实现

//第k层结点的个数
int TreeKLevelSize(BTNode* root, int k)
{
	if (k < 1 || root == NULL)//空树或输入k值不合法
		return 0;
	if (k == 1)//第一层结点个数
		return 1;
  //不为空且合法时，第K层的结点个数=第K-1层的左子树结点个数+第K-1层的右子树结点个数
	return TreeKLevelSize(root->left, k - 1) + TreeKLevelSize(root->right, k - 1);
}

测试

10、计算树的最大深度

计算树的最大深度时，可以将问题拆成子问题
1、为空时，深度为0
2、不为空时，最大深度为左子树和右子树较大的深度+1(自己)

代码实现

int maxDepth(BTNode* root) {
	if (root == NULL)
		return 0;//为空，深度为0
	int leftDepth = maxDepth(root->left);//记录左子树最大深度
	int rightDepth = maxDepth(root->right);//记录右子树最大深度
    //不为空时，最大深度为左子树和右子树较大的深度+1(自己)
	return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;
}

测试

总结

本篇博客就结束啦，谢谢大家的观看，如果公主少年们有好的建议可以留言喔，谢谢大家啦！