Leetcode学习之120. 三角形最小路径和 (经典动态规划)

思路:这道题其实属于一个问题基于上一个问题的解,也就是一个大的问题可以不断分割成一个一个的小问题,从而对总的问题求一个最优解,是很适合动态规划的。因此,由于是一个三角形,我们可以用一个二维数组作为我们的dp[][],对每一个子问题进行记录,求解,从而一步一步得出最短路径。
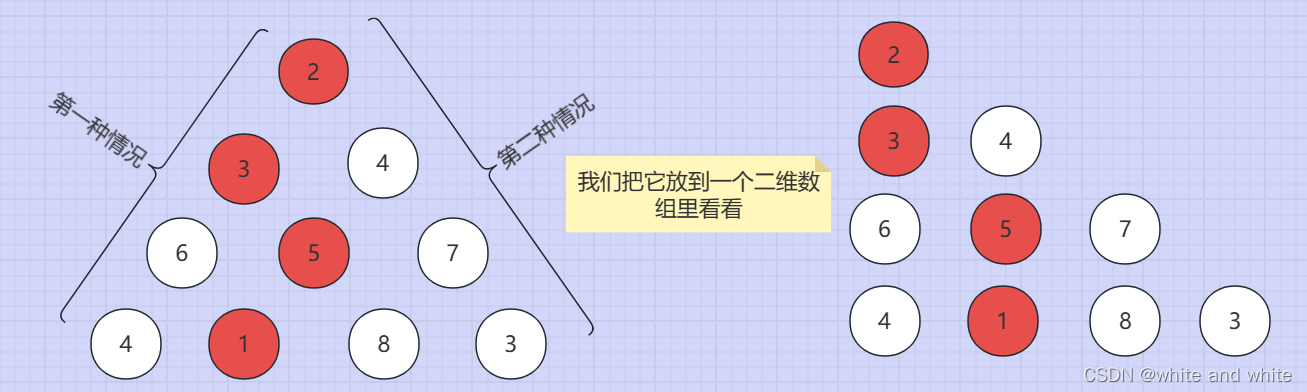
先来看下图第一种情况:每层的最左节点他有且只有一个父亲节点,假设每个节点的下标为 num[i][j],可以他到最左节点的父节点的 j 都是一样的且都是0 ,节点2 为 nums[0][0],节点3为nums[1][0],节点6为nums[2][0]以此类推
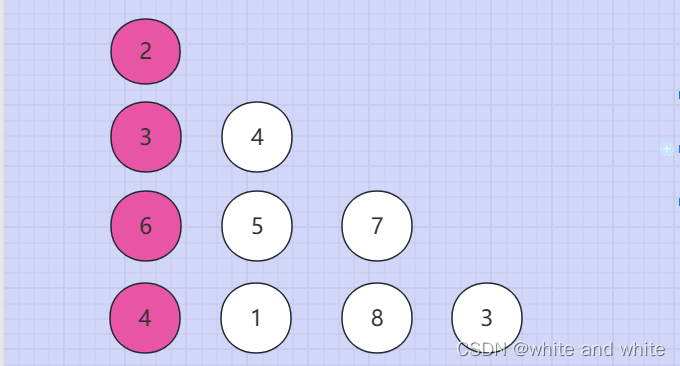
接着下图就是第二种情况。每层的最右节点有且只有一个父亲节点,假设每个节点的下标为 num[i][j],可以观察到最右节点的父节点的 i 和 j 为i -1,j-1 的,节点2 nums[0][0],节点 nums[1][2]…以此类推
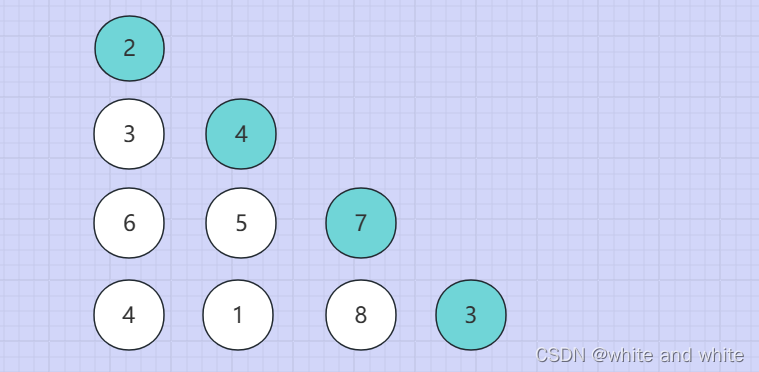
最后第三种情况:每个节点都有两个父亲节点,假设每个节点的下标为 num[i][j],可以观察到节点的父节点的 i 和 j 为i -1,j-1 或者 i 和j-1
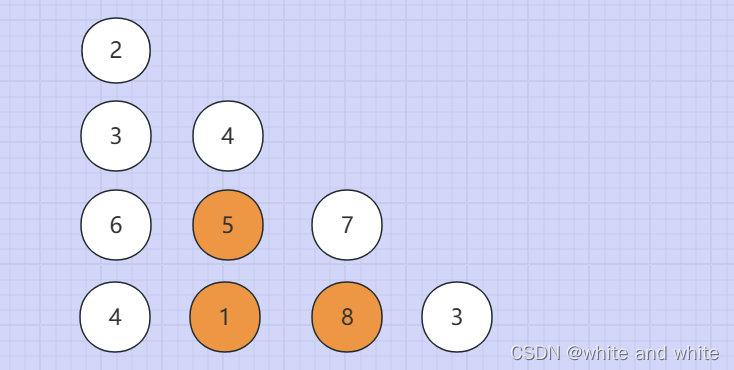
由此,我们可以列出如下动态转移方程:
* dp[0][0] = List.get(0).get(0); 第一个元素(初始元素)
* dp[i][j] = Min(dp[i][j-1],dp[i-1][j-1]) + List.get(i).get(j) 这是针对有左右父节点的元素
* dp[i][j] = dp[i][j-1] + List.get(i).get(j) 这是针对每层左节点,也就是j = 0的情况
* dp[i][maxIdx] = dp[i-1][j-1] + List.get(i).get(j) 这是针对每层最右节点,也就是j = 当前层最大idx的情况
接下来代码的问题也就一下解决了:
public static int minimumTotal(List<List<Integer>> triangle) {
//找出三角形最下层长度
int len = triangle.size();
int width = triangle.get(len - 1).size();
//新建dp矩阵
int[][] dp = new int[width][width];
dp[0][0] = triangle.get(0).get(0);
//最小值初始化
int min = dp[0][0];
//开始遍历三角形
for(int i = 1;i < len;i++){
//获取每一层
int size = triangle.get(i).size();
for(int j = 0;j < size;j++){
//遍历dp,第一种处于边界,也就是只有一个点可以到达
if(j == 0){
dp[i][j] = dp[i-1][j] + triangle.get(i).get(j);
}
//第三种每层最右节点
else if(j == size-1){
dp[i][j] = dp[i-1][j-1] + triangle.get(i).get(j);
}
//第三种,有左右父节点可以到达
else{
dp[i][j] = Math.min(dp[i-1][j-1],dp[i-1][j]) + triangle.get(i).get(j);
}
//最后一层需要对比min
if(i == len-1&&j==0){
min = dp[i][j];
}else if(i == len-1&&j!=0){
min = Math.min(dp[i][j],min);
}
}
}
return min;
}
这只是最经典的动态规划解决,其实还有dp+空间优化,可以看到我们的矩形其实只占用了一半的空间,而且每个子问题只会与上一个**dp[i][j-1],dp[i-1][j-1]**相关,其他的都是无关的,我们可以替换掉这些无关变量,以达到O(n)的空间复杂度
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- scala方法与函数
- 基于SSM的旅游管理系统论文
- SpringBean生命周期是怎样的?
- JavaSE 万字总结知识点(期末复习指南)
- 【Linux】深挖进程地址空间
- 【每日论文阅读】生成模型篇
- 【C++干货铺】会搜索的二叉树(BSTree)
- 代码随想录算法训练营第三十六天| 435.无重叠区间、763.划分字母区间、56.合并区间
- 【学习】将一个文件夹中所有的文件夹按照顺序编号重命名
- 二、安全与风险管理—信息安全治理