11.3、信赖域策略优化算法TRPO强化学习-运用实践

基于LunarLander登陆器的TRPO强化学习（含PYTHON工程）

TRPO强化学习算法主要分为3个部分，分别介绍其理论、细节、实现

本文主要介绍TRPO的理论和代码的对应、实践

TRPO系列（TRPO是真的复杂，全部理解花费了我半个月的时间嘞，希望也能帮助大家理解一下）：
11.1、信赖域策略优化算法TRPO强化学习-从理论到实践
11.2、信赖域策略优化算法TRPO强化学习-约束优化求解
11.3、信赖域策略优化算法TRPO强化学习-运用实践

其他算法：
07、基于LunarLander登陆器的DQN强化学习案例（含PYTHON工程）

08、基于LunarLander登陆器的DDQN强化学习（含PYTHON工程）

09、基于LunarLander登陆器的Dueling DQN强化学习（含PYTHON工程）

10、基于LunarLander登陆器的Dueling DDQN强化学习（含PYTHON工程）

11、基于LunarLander登陆器的A2C强化学习（含PYTHON工程）

参考：
【TRPO系列讲解】（五）TRPO_理论推导篇

1、替代优势函数的计算

信赖域策略优化算法TRPO强化学习-从理论到实践中介绍了TRPO的核心函数：替代优势函数。
要优化的式子是：
$$\begin{array}{l}{\max }_{\theta }{L}_{{\theta }_{old}}(\theta )={\max }_{\theta }E{}_{s～{\rho }_{{\theta }_{old}},a～{\theta }_{old}}\left[\frac{{\pi }_{\theta }(a\mid s)}{{\pi }_{{\theta }_{old}}(a\mid s)}{A}_{{\theta }_{old}(s,a)}\right]\\ subjectto{E}_{s～{\rho }_{{\theta }_{old}}}\left[D_{KL}({\pi }_{{\theta }_{old}}(?\mid s)\parallel {\pi }_{\theta }(?\mid s))\right]\le \delta \end{array}$$

替代优势函数$L_{{\theta }_{old}}(\theta )$的表达式为：
$$L_{{\theta }_{old}}(\theta )=E{}_{s～{\rho }_{{\theta }_{old}},a～{\theta }_{old}}\left[\frac{{\pi }_{\theta }(a\mid s)}{{\pi }_{{\theta }_{old}}(a\mid s)}{A}_{{\theta }_{old}(s,a)}\right]$$
其中：
$$A_{\pi }(s,a)=Q_{\pi }(s,a)?V_{\pi }(s)$$

对应核心代码（考虑到熵实际上是额外的改进了）：

	# 计算新旧动作概率之比，即当前策略与旧策略在给定状态下的动作选择概率之比
	prob_ratio = action_prob / old_action_prob  # pi(a|s) / pi_old(a|s)
	# 计算替代损失。这个损失主要由两部分组成：1) 基于新旧策略的动作概率之比的收益；2) entropy正则化项，由self.ent_coeff控制权重。
	loss = tf.reduce_mean(prob_ratio * advantage) + self.ent_coeff * entropy

状态价值函数V可以通过批评者网络得到，但是Q函数在TRPO中属于未知的，在此使用$U_t$近似，其原因如下：

Q(s,a)和Ut关系：Q(s,a)是Ut的期望，期望可以理解为求积分，实际上Q是对Ut把所有t之后的时刻（t+1、t+2等等）当作变量求积分得到的。因此Q(s,a)可以直观反应当前状态s下执行各个动作的好坏。
$$Q_{\pi }(s_t,a_t)=\mathbb{E}[U_t\mid s_t,a_t]$$

由此替代优势函数的计算的代码表达如下（代码里面叫surrogate_loss，其实是一样的）：

# 计算状态价值函数
Vs = self.value_model(obs).numpy().flatten()
# 计算优势函数,Gs就是Ut
advantage = Gs - Vs
# 直接标准化
advantage = (advantage - advantage.mean())/(advantage.std() + 1e-8)
actions_one_hot = tf.one_hot(actions, self.envs[0].action_space.n, dtype="float64")
# 计算其替代函数L的损失
policy_loss = surrogate_loss()

def surrogate_loss(theta=None):
	# 如果theta为None，则使用self.model作为模型，否则使用self.tmp_model并为其赋值
	if theta is None:
		model = self.model
	else:
		model = self.tmp_model
		assign_vars(self.tmp_model, theta)
	# 使用模型对obs进行预测，得到logits
	logits = model(obs)
	# 对logits应用softmax函数，得到action的概率分布
	action_prob = tf.nn.softmax(logits)
	# 计算每个动作的概率之和，这里假设actions_one_hot是动作的one-hot编码
	action_prob = tf.reduce_sum(actions_one_hot * action_prob, axis=1)
	# 使用原始模型对obs进行预测，得到旧的logits
	old_logits = self.model(obs)
	# 对旧的logits应用softmax函数，得到旧的动作概率分布
	old_action_prob = tf.nn.softmax(old_logits)
	# 计算每个动作的旧概率之和，并加上一个小的常数以避免除以0的错误
	old_action_prob = tf.reduce_sum(actions_one_hot * old_action_prob, axis=1).numpy() + 1e-8
	# 计算新旧动作概率之比，即当前策略与旧策略在给定状态下的动作选择概率之比
	prob_ratio = action_prob / old_action_prob  # pi(a|s) / pi_old(a|s)
	# 计算替代损失。这个损失主要由两部分组成：1) 基于新旧策略的动作概率之比的收益；2) entropy正则化项，由self.ent_coeff控制权重。
	loss = tf.reduce_mean(prob_ratio * advantage) + self.ent_coeff * entropy
	# 返回计算得到的损失值。
	return loss

2、替代优势函数导数的计算

信赖域策略优化算法TRPO强化学习-约束优化求解的第2部分中，替代优势函数的导数在更新中扮演着十分重要的作用，需要进行求解：
$$g^T={?}_{\theta }{L}_{{\theta }_{old}}(\theta ){|}_{\theta ={\theta }_{old}}$$
$${\theta }^{\prime }=\sqrt{\frac{2\delta }{g^T{H}^{?1}g}}{H}^{?1}g+\theta$$

其对应的代码为：

# 计算替代优势函数的导数g
policy_gradient = flatgrad(surrogate_loss, self.model.trainable_variables).numpy()

其中，flatgrad是求导的函数，在代码中会多次用到：

# Makes gradient of function loss_fn wrt var_list and
# flattens it to have a 1-D vector 计算梯度，并将其扁平化
def flatgrad(loss_fn, var_list):
	with tf.GradientTape() as t:
		loss = loss_fn()
	grads = t.gradient(loss, var_list, unconnected_gradients=tf.UnconnectedGradients.ZERO)
	return tf.concat([tf.reshape(g, [-1]) for g in grads], axis=0)

3、海森向量积的计算

对于TRPO的不等式约束，我们对其使用二阶泰勒展开（证明参考自然梯度Natural Policy）：
$$\begin{array}{r}\overline{D_{KL}^{{\rho }_{old}}}({\pi }_{old},{\pi }_{new})\to \frac{1}{2}(\theta ?{\theta }_{old}{)}^{T}A({\theta }_{old})(\theta ?{\theta }_{old})\\ \\ H=A({\theta }_{old})={?}_{\theta }^2\overline{D_{KL}^{{\rho }_{old}}}({\pi }_{old},{\pi }_{new})\end{array}$$

此外，我们需要使用共轭梯度法求解$H^{?1}g$矩阵，这等价于求解线性方程$Hx=g$，需要频繁使用到海森矩阵H和向量x的乘积。而且，海森矩阵需要对KL散度求二阶导得到，这是一个相对复杂的过程。【TRPO系列讲解】（六）TRPO_求解实现篇的第12min介绍了一种简单的运算加速方式，就是先对KL散度求一阶导数，然后乘以向量x，然后再对相乘后的式子求导：
$$\begin{array}{rl}& H_{ij}=\frac{?}{?{\theta }_j}\frac{?D_{KL}}{?{\theta }_i}\\ & y_i=\frac{?}{?\theta }\sum _j\frac{?D_{KL}}{?{\theta }_j}{x}_j\\ & y_k=\sum _j{H}_{kj}{x}_j=\sum _j\frac{?}{?{\theta }_j}\frac{?D_{KL}}{?{\theta }_k}{x}_j\\ & =\frac{?}{?{\theta }_k}\sum _j\frac{?D_{KL}}{?{\theta }_j}{x}_j\end{array}$$

对应代码如下：

# 计算Hessian向量积
def hessian_vector_product(p):
	# 此处的p实际输入的是x
	def hvp_fn():
		# 使用flatgrad函数计算kl_fn损失函数关于模型可训练变量的梯度，得到一个扁平化的梯度数组kl_grad_vector
		kl_grad_vector = flatgrad(kl_fn, self.model.trainable_variables)
		# 计算梯度向量与给定向量p的点积，并将结果存储在grad_vector_product中
		grad_vector_product = tf.reduce_sum(kl_grad_vector * p)
		# 返回grad_vector_product的值
		return grad_vector_product

	# 使用flatgrad函数计算hvp_fn内部函数关于模型可训练变量的梯度，得到一个扁平化的梯度数组fisher_vector_product
	fisher_vector_product = flatgrad(hvp_fn, self.model.trainable_variables).numpy()
	# 返回fisher_vector_product的值，并加上cg_damping与向量p的乘积？
	return fisher_vector_product + (self.cg_damping * p)

4、共轭梯度法求解$H^{?1}g$

信赖域策略优化算法TRPO强化学习-约束优化求解的第4部分提到了，我们需要使用共轭梯度法求解$H^{?1}g$矩阵，这等价于求解线性方程$Hx=g$，需要频繁使用到海森矩阵H和向量x的乘积，这实际上是残差的计算。

其中policy_gradient 是对替代优势函数的导数，也就是g。hessian_vector_product函数作为conjugate_grad函数的第一个输入Ax，之后再调用Ax§计算海森矩阵和向量p的乘积。（至始至终都没有单独计算过海森矩阵的值，都是计算的海森矩阵和向量的乘积）

对共轭梯度法不了解的参考我的另一个博客：最速下降法、梯度下降法、共轭梯度法—理论分析与实践

代码中step_direction 其实就是要计算的$H^{?1}g$矩阵。

# 计算替代优势函数的导数g
policy_gradient = flatgrad(surrogate_loss, self.model.trainable_variables).numpy()
# 使用共轭梯度法
step_direction = conjugate_grad(hessian_vector_product, policy_gradient)

		# 共轭梯度法
		def conjugate_grad(Ax, b):
			"""
			Conjugate gradient algorithm
			(see https://en.wikipedia.org/wiki/Conjugate_gradient_method)
			"""
			x = np.zeros_like(b)
			r = b.copy() # Note: should be 'b - Ax(x)', but for x=0, Ax(x)=0. Change if doing warm start.
			p = r.copy()
			old_p = p.copy()
			r_dot_old = np.dot(r,r)
			for _ in range(self.cg_iters):
				z = Ax(p)
				alpha = r_dot_old / (np.dot(p, z) + 1e-8)
				old_x = x
				x += alpha * p
				r -= alpha * z
				r_dot_new = np.dot(r,r)
				beta = r_dot_new / (r_dot_old + 1e-8)
				r_dot_old = r_dot_new
				if r_dot_old < self.residual_tol:
					break
				old_p = p.copy()
				p = r + beta * p
				if np.isnan(x).any():
					print("x is nan")
					print("z", np.isnan(z))
					print("old_x", np.isnan(old_x))
					print("kl_fn", np.isnan(kl_fn()))
			return x

5、计算策略网络的更新步长

信赖域策略优化算法TRPO强化学习-约束优化求解的第3部分提到了，在TRPO算法中，其更新公式为：
$${\theta }^{\prime }=\sqrt{\frac{2\delta }{g^T{H}^{?1}g}}{H}^{?1}g+\theta$$

$H^{?1}g$的数值我们可以通过共轭梯度法进行求解，那我们该如何计算更新的参数呢？

# 计算替代优势函数的导数g
policy_gradient = flatgrad(surrogate_loss, self.model.trainable_variables).numpy()
# 使用共轭梯度法，step_direction 是H-1*g
step_direction = conjugate_grad(hessian_vector_product, policy_gradient)
# 中间变量，计算的是
shs = .5 * step_direction.dot(hessian_vector_product(step_direction).T)

lm = np.sqrt(shs / self.delta) + 1e-8
fullstep = step_direction / lm

根据如上的代码：
$$\begin{array}{l}shs=\left(\frac{1}{2}{H}^{?1}g\right){\left(H{H}^{?1}g\right)}^T=\frac{1}{2}{g}^T{H}^{?1}g\\ lm=\sqrt{\frac{g^T{H}^{?1}g}{2\delta }}\\ fullstep=\frac{H^{?1}g}{\sqrt{\frac{g^T{H}^{?1}g}{2\delta }}}=\sqrt{\frac{2\delta }{g^T{H}^{?1}g}}{H}^{?1}g\end{array}$$

和更新数据一致。

6、更新步长回溯衰减

但是，信赖域策略优化算法TRPO强化学习-约束优化求解的第5部分提到了，TRPO使用了太多的近似，理论的方程并不一定是最好的，那我们我们该如何做呢？我们可以选择小于 $\alpha$的学习率多次尝试（如$0.9^1\alpha$、$0.9^2\alpha$、$0.9^3\alpha$、$0.9^4\alpha$…），直到找到一个能够提升替代优势$L_{{\theta }_{old}}(\theta )$的学习率，这个过程被称为LineSearch：

	# 在给定方向上找到函数的局部最小值，最优化算法
	def linesearch(x, fullstep):
		# fval = surrogate_loss(x)
		for (_n_backtracks, stepfrac) in enumerate(self.backtrack_coeff**np.arange(self.backtrack_iters)):
			xnew = x + stepfrac * fullstep
			newfval = surrogate_loss(xnew)
			kl_div = kl_fn(xnew)
			if np.isnan(kl_div):
				print("kl is nan")
				print("xnew", np.isnan(xnew))
				print("x", np.isnan(x))
				print("stepfrac", np.isnan(stepfrac))
				print("fullstep",  np.isnan(fullstep))
			if kl_div <= self.delta and newfval >= 0:
				print("Linesearch worked at ", _n_backtracks)
				return xnew
			if _n_backtracks == self.backtrack_iters - 1:
				print("Linesearch failed.", kl_div, newfval)
		return x

7、基于LunarLander登陆器的TRPO强化学习（含PYTHON工程）

基于TensorFlow 2.10

主要代码来自github上的一位小哥，但是原来的效果太差了：

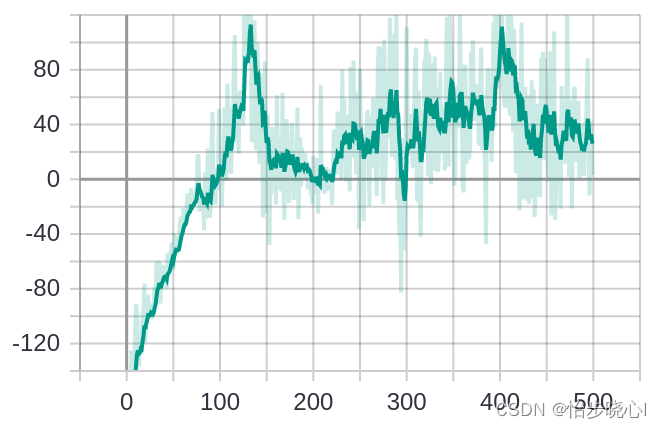
我稍微修改优化了一下，下面的两张图第一个是每次运行的得分，第二张为均值平滑后的曲线，因为使用了wandb，实际上运行了大约300个episode，作者原来的因该是运行500个episode的结果嘞（LR是价值网络的学习率，因为使用了自然梯度法，策略网络的学习率无需手动设置）。优化后基本能跑个200多分，算是还可以吧。

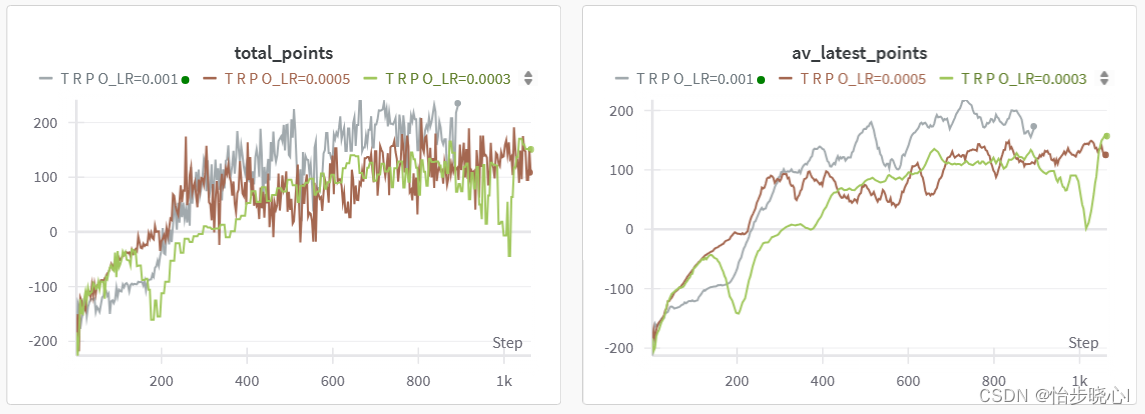
工程可以从最上方链接下载，喜欢就点个赞吧。