MATLAB - 四元数（quaternion）

系列文章目录

前言

一、简介

四元数是一种四元超复数，用于三维旋转和定向。

四元数的表示形式为 a+bi+cj+dk，其中 a、b、c 和 d 为实数，i、j 和 k 为基元，满足等式：i2 = j2 = k2 = ijk =-1。

四元数集用 H 表示，定义在实数的四维向量空间 R4 中。H 中的每个元素都有一个基于基元素 i、j 和 k 线性组合的唯一表示。

三维空间中的所有旋转都可以用旋转轴和围绕该轴的角度来描述。与旋转矩阵相比，四元数的优势在于旋转轴和旋转角度易于解释。例如，考虑 R3 中的一个点。要旋转该点，需要定义一个旋转轴和一个旋转角度。

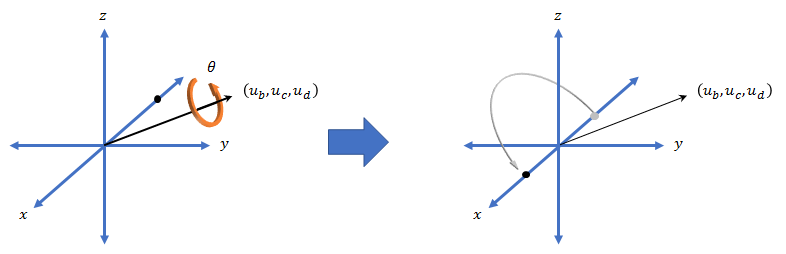
旋转的四元数表示可表示为 ，其中 θ 是旋转角度，[ub、uc 和 ud] 是旋转轴。) ，其中 θ 是旋转角度，[ub、uc 和 ud] 是旋转轴。

二、MATLAB 用法?

quat = quaternion()
quat = quaternion(A,B,C,D)
quat = quaternion(matrix)
quat = quaternion(RV, "rotvec")
quat = quaternion(RV, "rotvecd")
quat = quaternion(RM, "rotmat",PF)
quat = quaternion(E, "euler",RS,PF)
quat = quaternion(E, "eulerd",RS,PF)
quat = quaternion(transformation)
quat = quaternion（rotation）

?三、四元数的优点

1.非奇异表达（和例如欧拉角之类的表示相比）

2.比矩阵更紧凑（更快速）

3.单位四元数的对可以表示四维空间中的一个转动。