Seer*Stat乳腺癌数据预测模型-Step3特征选择

Seer*Stat乳腺癌数据预测模型-Step3特征选择

这里特征选择我采用了三种方法，基于方差阈值，主成分分析和ExtraTreesClassifier这三种方法进行特征选择，最后通过比较同一个模型的准确率和召回率来确定最后的一些特征。

方差阈值法

方差：顾名思义，在一个单一的度量中显示分布的可变性。它显示了分布是如何分散的，并显示了平均距离的平方: 使用零方差的特性只会增加模型的复杂性，而不会增加它的预测能力。相当于这个特征没有发生变化，每个特征都是相同的值而对最后的结果并没有什么影响。

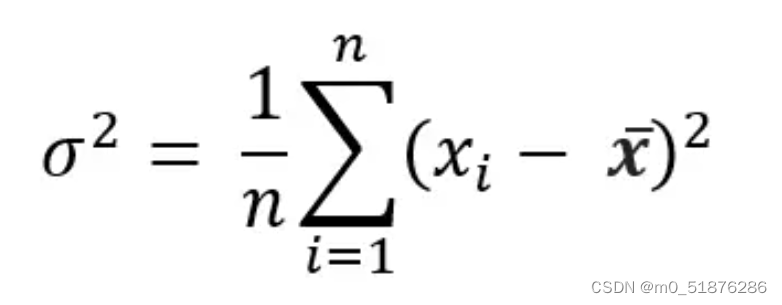
比较方差和特征归一化，将特征值除以均值来进行归一化。

from sklearn.feature_selection import VarianceThreshold
vt=VarianceThreshold()#需要将数字特征放到同一个数据集中，因为估计器无法识别分类特征。
df_number=df.select_dtypes(include="number")
#transformed=vt.fit_transform(df_number)
_ = vt.fit(df_number)
mask = vt.get_support()
df_number=df_number.loc[:,mask]
print(f'df的shape:{df.shape},df_number的shape:{df_number.shape}')
df_normal=df_number/df_number.mean()
print(df_normal.var())

vt=VarianceThreshold(threshold=0.2)
_ = vt.fit(df_normal)
mask = vt.get_support()
df_final=df_number.loc[:,mask]
print(df_final.columns)
lable1=list(df_final.columns)
lable1=['ajcc', 'Psite', 'cs', 'rx', 'Survival.month']

将参数设置为0.2，特征选择为`‘Psite’,‘ajcc’,‘cs’,‘rx’,‘survial.month’

主成分分析法

主成分分析法是一种常见的数据分析方式，常用于高维数据的降维，可用于提取数据的主要特征分量。PCA通常用于降低大型数据集的维数，方法是数据集中的指标数量变少，并且保留原数据集中指标的大部分信息。总而言之：减少数据指标数量，保留尽可能多的信息。`

components_: 选定的主成分。是一个形状为 (n_components, n_features) 的数组，表示每个主成分的特征向量。
explained_variance_: 每个主成分的解释方差。它是一个包含了按降序排列的每个主成分的解释方差值的一维数组。
explained_variance_ratio_: 每个主成分的解释方差比例。它是一个包含了按降序排列的每个主成分的解释方差比例的一维数组。
n_components: 这个参数决定了PCA算法应该保留的主成分数量。如果设置为None（默认值），则保留所有主成分。如果设置为一个整数k，则只保留前k个主成分；k为小数表示保留的主成分的方差百分比。通过选择适当的主成分数量，可以实现数据的降维。

如何使用这些函数和属性得到提取的特征值：我们调用fit函数之后会得到n_components组数据存放在components_中，再将每一组中的主成分中的最大的特征选择出来就是经过PCA提取的特征

from sklearn.decomposition import PCA
pca=PCA()
pca.fit(df[lable[:-1]])
cumsum=np.cumsum(pca.explained_variance_ratio_)
d=np.argmax(cumsum>=0.95)+1
print(d)#d=4
model=PCA(n_components=4).fit(df[lable[:-1]])
x_pc=model.transform(df[lable[:-1]])
n_pcs=model.components_.shape[0]
print(f"components_={model.components_}")
print(f"n_pcs={n_pcs}")
most_important = [np.abs(model.components_[i]).argmax() for i in range(n_pcs)]#选择这四个组中每个组中最大的一个特征。
print(f"most_important={most_important}")
most_important_names = [lable[most_important[i]] for i in range(n_pcs)]
dic = {'PC{}'.format(i): most_important_names[i] for i in range(n_pcs)}
end=pd.DataFrame(dic.items())
print(end)

lable2=[‘Survial.month’,‘cs’,‘rx’,‘Dage’]

极度随机树

极度随机树ExtraTreesClassifier是一种集成学习技术，它将森林中收集的多个去相关决策树的结果聚集起来输出分类结果。极度随机树的每棵决策树都是由原始训练样本构建的。在每个测试节点上，每棵树都有一个随机样本，样本中有k个特征，每个决策树都必须从这些特征集中选择最佳特征，然后根据一些数学指标(一般是基尼指数)来拆分数据。这种随机的特征样本导致多个不相关的决策树的产生。

# from sklearn.ensemble import ExtraTreesClassifier
# clf=ExtraTreesClassifier()
# etc=clf.fit(train_x,train_y)
# print(etc.feature_importances_)
# plt.bar(lable[:-1],etc.feature_importances_)
# plt.show()

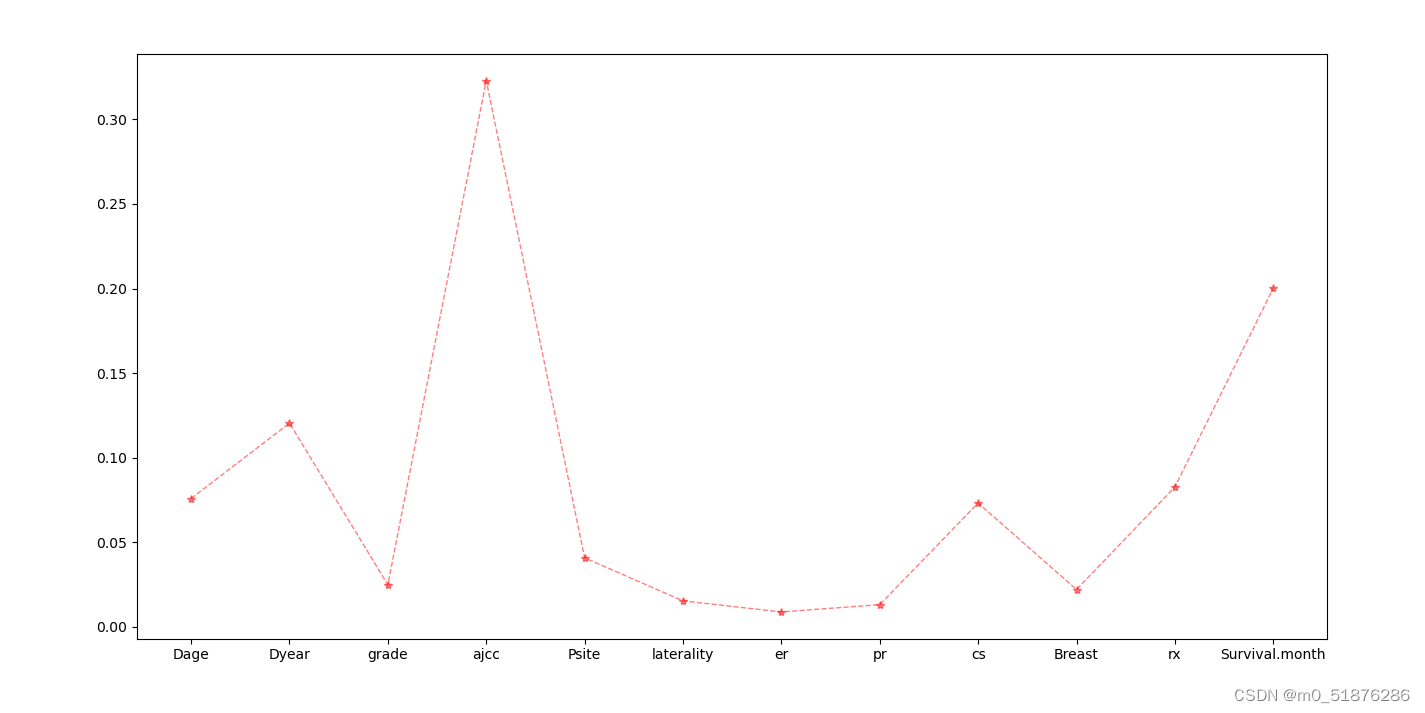
lable3=[‘Dage’, ‘Dyear’, ‘ajcc’, ‘cs’,‘rx’, ‘Survival.month’]

最后选择第三类特征。