二叉树进阶oj题目

二叉树进阶oj题目

• 两个结点的最近公共祖先
• 前序中序（中序后序）还原二叉树

1、两个结点的最近公共祖先（两种方法）

leetcode链接
题目描述：给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”如下图所示：

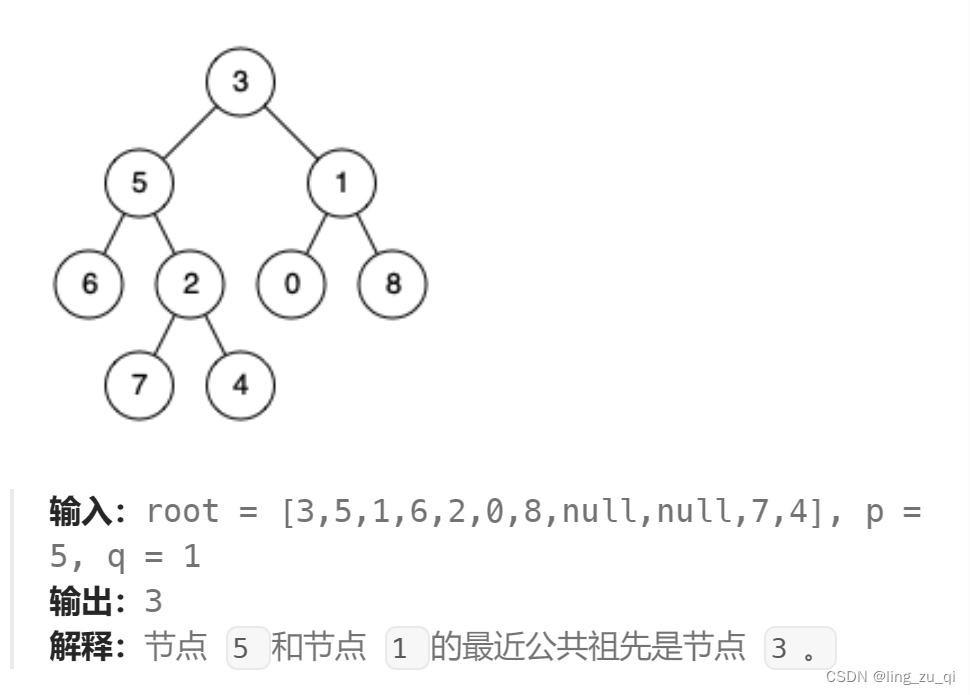
对于这个问题，有两种方法可以解决。
方法一：分类讨论
思考一下，p和q结点相较于最初的根结点root的位置有哪几种情况？

• 1、p和q结点中的一个是root结点
• 2、p和q结点分别在root结点的左右子树中
• 3、p和q结点都在root结点的一颗子树中

对于情况1，p和q结点的最近公共祖先必然为root，直接返回root即可。
对于情况2，p和q的最近公共祖先也为root，直接返回root即可。
对于情况3，我们需要对于root结点的左孩子和右孩子递归调用这个寻找公共祖先的方法，如果两个方法得到的返回值都不为空，返回当前结点即可。否则，返回非空的那个结点。（不存在两个都为空的情况）。以下是代码的呈现：

public TreeNode lowestCommonAncestor(TreeNode root,TreeNode p,TreeNode q) {
        if(root==null) return null;
        if(q==root) return q;//找到了结点就返回
        if(p==root) return p;
        TreeNode retleft = lowestCommonAncestor(root.left,p,q);//左孩子递归
        TreeNode retright = lowestCommonAncestor(root.right,p,q);//右孩子递归
        if(retleft!=null&&retright!=null) {
            return root;
        }else if(retleft==null) {
            return retright;
        }else {
            return retleft;
        }
}

方法二：记录路径
实际上，我们只要能够**记录下根节点到p结点和q结点的路径，这两个路径事实上是两个链表，这个问题就可以转化成两个链表相交的问题。**由于二叉树的结点并没有parent引用，无法从下往上将路径贯通，那我们该如何来记录路径呢？**我们使用的思路类似于dfs（深度优先搜索），同时使用栈这种数据结构，一条条路径去尝试。**对于非叶子结点，将左孩子结点入栈，不断递归判断是否为p或q，是p或q结点就返回，否则直到叶子节点开始返回，将不在所求路径上的结点出栈，并将右孩子结点放入。在将结点反复地出入栈后，最后栈里留下的就是root到p或q结点的路径。（p和q结点的路径需要分别存放在两个栈中）。
代码如下：

 public boolean getPath(TreeNode root, TreeNode node,
                           Stack<TreeNode> stack) {
        if(root == null) {
            return false;
        }
        stack.push(root);
        if(root == node) {
            return true;
        }
        boolean flgLeft = getPath(root.left,node,stack);
        if(flgLeft) {
            return true;
        }
        boolean flgRight = getPath(root.right,node,stack);
        if(flgRight) {
            return true;
        }
        stack.pop();
        return false;
    }

接下来，就是处理链表相交结点的问题，解决步骤：
1、计算两个栈（链表）的大小之差diff（大-小）
2、将较大的栈（链表）中diff个元素出栈（尾删）
3、当两个栈（链表）不为空时，遍历比较栈顶（链表头）的元素，相同则直接返回，不同则分别出栈（尾删），重复操作直到相同。

2、前序中序（中序后序）还原二叉树

前序中序：leetcode链接
中序后序：leetcode链接
在讲解这道题目前，我们要对二叉树的前序、中序和后序遍历有一个更深刻的了解。
我们先来对前序和中序遍历还原二叉树的过程做一个模拟。比如说我们有一个前序和中序的二叉树遍历序列：
preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
我们要做的就是从前到后遍历preorder，而inorder是用来确定左子树和右子树是由哪些部分构成的。我们来模拟一下这个过程：
1、preorder中第一个结点3，在inorder中3在下标1的位置，3的左边就是左子树，右边就是右子树
2、preorder中第二个结点9，在inorder中9在下标0的位置，9的左边没有数，左树为空，右边本来应该是3，但是3已经访问过了，所以9的右树也为空。

以此类推，我们就可以还原出整棵树。我们在还原过程中要用到四个参数，preorder序列，inorder序列，以及inBegin，inEnd来判断是否这个结点的子树是否还原完成，**初始值分别赋为0和preorder.length-1,**可以通过构建一个函数buildChildTree方法来实现。

  public int preIndex；//定义为静态成员变量，防止受到递归的影响
  public TreeNode buildTree(int[] preorder, int[] inorder) {
        return buildTreeChild(preorder,inorder,0,preorder.length-1);
  }

buildTreeChild方法实现步骤：
1、创建结点

   TreeNode root = new TreeNode(preorder[preIndex]);

2、中序遍历中找到当前结点下标

   int rootIndex = findRooIndex(inorder,inBegin,inEnd,preorder[preIndex]);
   preIndex++；

   public int findRooIndex(int[] inoder,int inBegin,int inEnd,int key) {
        for(int i=inBegin;i<=inEnd;i++) {
            if(inoder[i]==key) {
                return i;
            }
        }
        return -1;
    }

3、分别创建左右子树

   root.left = buildTreeChild(preorder,inorder,inBegin,rootIndex-1);
   root.right =buildTreeChild(preorder,inorder,rootIndex+1,inEnd);

4、判断条件：inBegin>inEnd，子树构建完毕，返回null
以结点9为例，root.left调用buildTreeChild方法后，这个方法内部，inBegin的值为0，inEnd的值为-1，左树为null，root.right调用buildTreeChild方法后，这个方法内部inBegin为1，inEnd为preorder.length-1，因为查找不到9，rootIndex返回-1。
下面是完整的代码呈现:

class Solution {
    public int preIndex;
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        return buildTreeChild(preorder,inorder,0,preorder.length-1);
    }
    public TreeNode buildTreeChild(int[] preorder,int[] inorder,int inBegin,int inEnd) {
        if(inBegin>inEnd) {
            return null;
        }
        //1、创建结点
        TreeNode root = new TreeNode(preorder[preIndex]);
        //2、中序遍历中找到当前结点下标
        int rootIndex = findRooIndex(inorder,inBegin,inEnd,preorder[preIndex]);
        preIndex++;
        //3、分别创建左右子树
        root.left = buildTreeChild(preorder,inorder,inBegin,rootIndex-1);
        root.right =buildTreeChild(preorder,inorder,rootIndex+1,inEnd);
        return root; 
    }
    public int findRooIndex(int[] inoder,int inBegin,int inEnd,int key) {
        for(int i=inBegin;i<=inEnd;i++) {
            if(inoder[i]==key) {
                return i;
            }
        }
        return -1;
    }
}

而对于后序中序还原二叉树，我们也可以按照这种思路模拟实现。唯一需要注意的是我们要从后向前遍历posorder这个序列，同时要先创建右子树，再创建左子树，这样才能符合二叉树后序遍历的顺序。下面直接呈现代码：

class Solution {
    public int postIndex;
    public TreeNode buildTree(int[] inorder, int[] postorder) {
        postIndex = inorder.length-1;
        return buildTreeChild(postorder,inorder,0,inorder.length-1);
    }
    public TreeNode buildTreeChild(int[] postorder,int[] inorder,int inBegin,int inEnd) {
        if(inBegin>inEnd) {
            return null;
        }
        //1、创建结点
        TreeNode root = new TreeNode(postorder[postIndex]);
        //2、中序遍历中找到当前结点下标
        int rootIndex = findRooIndex(inorder,inBegin,inEnd,postorder[postIndex]);
        postIndex--;
        //3、分别创建右左子树
        root.right =buildTreeChild(postorder,inorder,rootIndex+1,inEnd);
        root.left = buildTreeChild(postorder,inorder,inBegin,rootIndex-1);
        return root; 
    }
    public int findRooIndex(int[] inoder,int inBegin,int inEnd,int key) {
        for(int i=inBegin;i<=inEnd;i++) {
            if(inoder[i]==key) {
                return i;
            }
        }
        return -1;
    }
}