Probabilistic Concept Bottleneck Models (ProbCBM)

本篇文章发表于ICML 2023。

文章链接：https://arxiv.org/abs/2306.01574

代码链接：GitHub - ejkim47/prob-cbm: Official code for "Probabilistic Concept Bottleneck Models (ICML 2023)"

---

一、概述

? ? ? ? 对于基于概念的模型（CBM）而言，可靠的concept predictions对于模型的可信度是至关重要的，存在于数据中的ambiguity会严重损害模型的可靠性；然而，data中的ambiguity却是广泛存在的，CBM却“predicts concepts deterministically without considering this ambiguity”。

? ? ? ? 针对以上问题，本文提出ProbCBM——使用probabilistic concept embeddings，ProbCBM将concept prediction中的uncertainty进行建模，基于concept以及其对应的uncertainty为最终的prediction提供explanations；此外，由于class uncertainty来源于concept uncertainty，因此我们也可以使用concept uncertainty来解释class uncertainty。

（类似于standard NNs与Bayesian NNs的区别，前者的weights是deterministic的，而后者的weights遵循一个概率分布。）

? ? ? ? 在Introduction部分作者指出了post-hoc方法的不足：cannot entirely explain the model's prediction and provide approximate explanations in a human-understandable form, which may lead to incorrect explanations(Rudin, 2019.https://arxiv.org/abs/1811.10154).

? ? ? ? 而concept-based model如CBM有着它的不足，“The concept prediction in CBM is trained as deterministic binary classfication by using a dataset that includes concept labels indicating the existence 1 or non-existence 0 of a concept.”

? ? ? ? 然而，concept的存在与否有时是ambiguous的，比如下图这个例子：

? ? ? ? 这四幅图片都对应于同一种鸟，即绿松鸦（green jay）；然而，它们之间的concept却不共享、混淆、存在ambiguity，要么没有尾巴、要么没有肚子、要么颜色不统一。而当使用离散概念的时候，这个问题可能会进一步加剧；并且在实际标注概念的时候，为了减轻标注负担，通常将相同的concept分配给不同的图像，但是如上图所示这是不合理的，因为有些example并不包含所提供的概念；反过来，提供的概念也不一定足以解释一张图片；此外，data augmentation，比如随机裁剪也会引入一定的视觉歧义。

? ? ? ? ProbCBM将图像project到具有probabilistic distribution的concept embedding中，对概念的不确定性进行建模；随后，将concept embeddings投影为class embeddings, "Thus, the final class prediction is derived from concept prediction."

? ? ? ? 总之，ProbCBM不同于CBM在瓶颈层将concept表征为确定性的值/向量，而是使其服从一个概率分布，由此引入uncertainty，使得预测更加可靠。即，不仅提供concept prediction，还提供concept uncertainty。

Note：uncertainty有三种：(i) model uncertainty (comes from the model parameters); (ii) data uncertainty (comes from the noise of the data); (iii) distribution uncertainty. 而probabilistic embedding主要考虑的是data uncertainty——“where the representations of input samples are expressed as probabilistic distributions.”

---

二、方法

? ? ? ? 图像被映射为concept embedding space中的概率嵌入，之后probabilistic concept embedding又被映射到class embedding space。

????????越大的椭圆代表越多的ambiguity，不确定性也越高。

????????实心点代表concept的存在，×代表concept不存在，可以看到有些concept并不存在于图像中（或只存在于部分图像中），这就是所谓的ambiguity。

? ? ? ? 与CBM类似，ProbCBM有一个concept predictor以及一个class predictor；

????????训练数据具有形式：?（仍然需要annotation）

(i) Probabilistic Concept Modeling

A. Probabilistic conept embedding

Given an input ?, the concept predictor makes probabilistic concept embedding ??for each concept ?, which is formulated as a normal distribution with a mean vector and a diagonal covariance matrix.

????????where???and???represents the dimension of the concept embedding space.

??????????通过probabilistic embedding module (PEM)进行预测，every concept uses a shared backbone and individual PEMs.

B. Concept prediction

? ? ? ? 输入图像经过backbone得到对应的feature，将feature输入到PEM中，得到???个均值以及???个方差；然后我们在这???个分布中采样以得到每个concept在当前采样步下的representation，即 ?，；??在不同的采样时刻是不一样的。

? ? ? ? 采样得到 ??后，需要判断 ??对应的图像中是否真的存在概念??，即计算??；具体做法如下：

? ? ? ? 从???中采样 ??个点，

????????概念???存在于 ??的概率用Monte-Carlo estimation进行估计，

?

?

??????????is a learnable parameter and???represents a sigmoid function.

??????????and???are tainable anchor points in??.??represents the? dimension of the concept embedding space)

????????如果在时间步 ??采样得到的???距离???距离更近（Euclidean distance），则概念的存在概率增加；如果???距离???距离更近，则概念存在的概率降低。

(ii) Probabilistic Class Modeling

A. Class embedding

? ? ? ? 将时间步???下对每一个概念采样得到的???使用FC层投影到class embedding space，得到当前时间步???对应的class embedding??，??is the dimension of the class embedding space：

B. Class prediction

The logit for class?? is defined by the Euclidean distance between the class embedding for the image and a trainable anchor point for class??,??.

We obtain the class probabilities by applying softmax to the logits for overall classes. The classification probability is obtained via Monte-Carlo estimation:

????????where???is a learnable parameter.

????????由于 ??由?? 得来，?是在时间步???下对???采样得到的，因此 ??也相当于是采样得到的；最终的classification probability将同样由MC estimation得到，对应上面的公式。

??????????与 anchor point ??距离(Euclidean distance)越近，分类概率就越高。

(iii) Training and Inference

A. Training objective

We additionally use a KL divergence loss between the predicted concept embedding distributions and the standard normal distribution.

This prevents the variances from collapsing to zero and makes the distribution??have only salient information for predicting the probability that the concept c exists.

????????即，用KL散度作为正则项，使???趋近于标准正态分布，避免方差坍缩为0，并保证???只有用于预测概念存在的显著信息。

? ? ? ? Thus, the overall training loss for the concept predictor is expressed as:

? ? ? ? We?use a cross-entropy loss for training class predictor (?).

B. Training scheme

????????分别训练concept predictor与class predictor

????????首先用???训练concept predictor，用以实现从输入到concept embedding space的准确projection；

????????然后用???训练class predictor；Note：以概率???的概率将concept predictor预测并采样得到的???替换为anchor point (??or???)，以???的概率不替换；这样做可以防止class predictor使用incorrect concepts进行学习。

C. Inference

Inference can be done by approximating the probabilities via Monte-Carlo sampling or using ??as ??without sampling.——可以通过Monte-Carlo estimation来估计最终的概率值，或者直接使用高斯分布的均值作为???从而得到最终的概率值而不用采样。

(iv) Derivation of Uncertainty

????????ProbCBM利用probabilistic modeling，使我们能够直接从预测的概率分布中估计不确定性，而不需要采样。具体而言，使用协方差矩阵的行列式来量化uncertainty，因为行列式代表了概率分布的体积，体积越大，uncertainty越大。由于the distribution of the concept embedding是用diagonal covariance matrix来参数化的，所以每个概念 ??的不确定性可以用对角元素 ??的几何平均值来计算。

????????而class embedding ??是the concatenation of concept embedding，即

??????????的linear transformation:

????????因此，the class embeddings follow??,

????????where???and??

????????Hence, the determinant of?? serves as an uncertainty measure of class prediction.

(v) Architecture

---

三、实验及结果

使用合成的数据集进行实验：

??

1. 将0-9共10个数字分为五组，每组的两个数字有相同颜色；

2. 从其中四组中各抽取1个数字构成新的图像（图像中含有4个数字），并分为12个类别；

3. 每个数字就作为图像中的一个concept；

4. 为了增加diversity，可以随机抹除一个数字。

????????图（左）“concept 1”存在的概率为1；图（中）“concept 1”存在的概率为0（很自信），因为它检测到了0的存在，而有0就不可能有1（符合事实）；

????????图（右）既没有0也没有1，这个时候对于“concept 1”存在预测的概率虽然很小，但不确定性uncertainty很大。（模型在疑惑：怎么0和1都没有呢？）

? ? ? ? 👆通过遮挡，人为地引入ambiguity。观察遮挡前后分类概率和不确定度的变化，以及concept uncertainty的变化，发现遮挡后对应concept的不确定度提高。

? ? ? ? 并且，遮挡后在embedding space中对应的椭圆（黄色）更大，代表着不确定度更大。

? ? ? ? 👆Real-world datasets的实验结果。图中展示了在不同图像中可能导致的concept ambiguity；左侧鸟所有的概念都能较为清楚地观察到，而中间和右侧的鸟某些concept无法被观察到，表现为uncertainty增加。

? ? ? ? 👆人为改变图像使其ambiguous：例如裁剪或改变色调。这会影响原始图像中的某些concept（如物体被删除，或颜色改变），从而增加不确定度。

????????实验结果与预期相符。

????????👆leg color的两个anchor point；

????????如果图像中看不到leg，则体现为较大的椭圆，并且偏离anchor更远。

? ? ? ? 👆uncertainty越大，performance越差。

Intervention

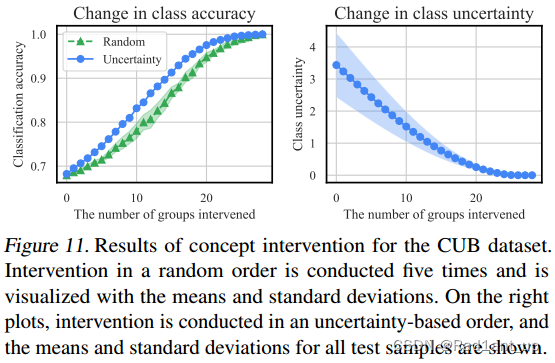
? ? ? ? 👆干预的concept越多，accuracy越高，class的不确定度越低。

? ? ? ? 👆干预的例子，红色为预测错误的concept，干预后分类结果正确。干预后，uncertainty相应的变为0，因为此时concept是人为确定的，不存在不确定度。

????????最后是本篇论文的一些讨论：

????????Limitations：和CBM类似，需要annotation，受人工标注质量的影响较大。

????????一个潜在的问题：图像中可能包含计算机能识别但人类无法理解的concept，但人类无法意识到，甚至会避免这种concept的出现，即使它们对于分类是有用的。