如何用离散二维卷积公式描述卷积过程（说实话，我没搞懂为什么索引为什么设置成对称的模式。）

发布时间：2024年01月05日

问题描述：如何用离散二维卷积公式描述卷积过程（说实话，我没搞懂为什么索引为什么设置成对称的模式。）

众所周知，描述图像卷积过程，可以使用图形法描述，也可以用公式法描述，但是具体用代码实现可能使用的for循环之类的，或者数组索引。

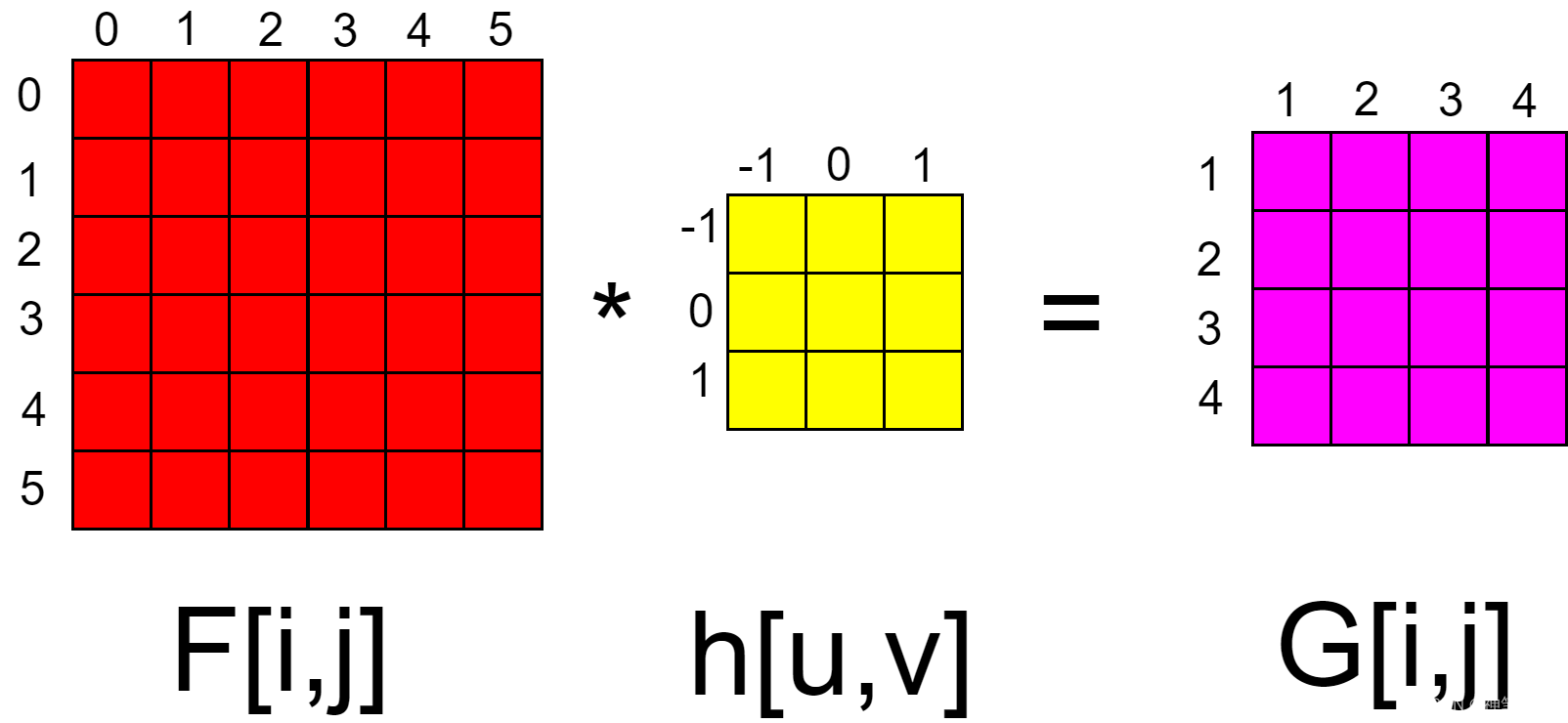
图像法描述卷积如下图所示。

描述：卷积时，以滑动窗口的形式，从左到右，从上到下，3个通道对应的位置相乘在求和。但是，在代码中，如何进行滑动的，还未知。

公式表示二维卷积过程。（为了解释方便这里仅展示二维卷积过程）

cross-correlation（互相关）公式表示如下：有网友说的卷积其实就是用的互相关。

G[i,j]=\sum_{u=-k}^{k}\sum_{v=-k}^{k}h[u,v]F[i+u,j+v]

实际上，Convolution?离散二维卷积运算公式和互相关cross-correlation类似，区别在于离散二维卷积将输入特征图进行了180度的翻转，公式如下。

G[i,j]=\sum_{u=-k}^{k}\sum_{v=-k}^{k}h[u,v]F[i-u,j-v]

其中输入特征图的索引被定义成了0，1，2，3，4，5，6；卷积核的索引被定义成了-1，0，1；输出特征图的索引被定义成了1，2，3，4。（至于为什么输入的索引从0开始，卷积核的索引是对称式，并且包含负数，输出特征图的索引从1开始，不得而知）

当i=1,j=1时，G[1,1]=

h[-1，-1]×F[2,2]+h[-1，0]×F[2,1]+h[-1，1]×F[2,0]+

h[0，-1]×F[1,2]+h[0，0]×F[1,1]+h[0，1]×F[1,0]+

h[1，-1]×F[0,2]+h[1，0]×F[0,1]+h[1，1]×F[0,0]

扩展一下成三维的卷积。

G[i,j]=\sum_{u=-k}^{k}\sum_{v=-k}^{k}\sum_{m=0}^{c}h[u,v,m]F[i-u,j-v,c-m]

事实上，普通卷积，如果只有一个卷积核，输入是三维，卷积核是三维，那么输出是二维的。

文章来源:https://blog.csdn.net/weixin_43501408/article/details/135413451
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
最新文章