【考研数学】03早鸟课 函数极限计算（3）泰勒公式求极限

文章目录

一、【黄金重点】和取低阶原则（有限个无穷小相加减）

二、高阶无穷小运算法则?

三、等价无穷小的充分必要条件

四、泰勒公式及介绍

五、泰勒公式的用法（展开原则）

原则1：相消不为0原则

【考】补充5个重点等价无穷小公式（由泰勒公式推出）

原则2：上下同阶原则（经验原则）

六、和取低阶原则易错点

八、最后真题应用

---

不同于教材的枯燥严谨，本文章旨在帮助研友快速接触考研数学，进入备考状态，基于考研内容进行学习。一些定义可能是出于对知识的应用，以做题应试为目的，而非课本准确定义。所以，对于零基础、期末备考以及考研新手同学非常友好！希望能成为大家做题的指导书。

?下面开始讲知识点3，想要看知识点1 极限定型 内容的同学，请移步：

【考研数学】01早鸟课 函数极限计算（1）

想要看知识点2 等价无穷小代换（无穷小量）?内容的同学，请移步：?

【考研数学】02早鸟课 函数极限计算（2）等价无穷小代换

---

一、【黄金重点】和取低阶原则（有限个无穷小相加减）

内容如下：

f(x) = o[g(x)],规定f(x)为g(x)高阶无穷小。用记号o

解释：当有 有限个无穷小 相加减时，最终取（等价于）最低阶的式子，即“和取低阶原则”

那到底是不是这样呢？我们来证明一下

要想知道是不是等价无穷小，只需把两者作比，结果为1就行。

简单应用例子：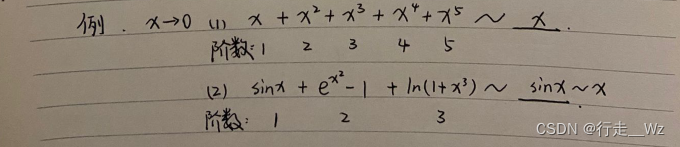

下面看一下这个原则的应用，到底在真题中如何考察

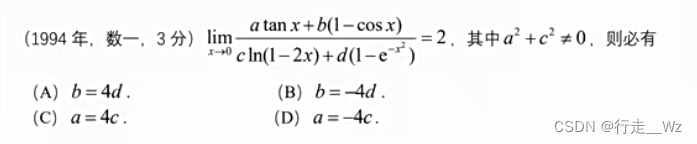
答案如下：

【分析答案】

因为分子分母涉及到加减法等价无穷小代换（不清楚的，可以去最上面找，我放了链接），所以能不能代换还需判断，而本题这里并没有直接代换掉，而是想看一下无穷小的阶数。

然后，利用“和取低阶原则”，将阶数小的项保留下来。本步是利用“和取低阶原则”删掉某些项，而不是等价无穷小直接代换。加减法等价无穷小代换是有条件的（不清楚的，可以在最上面找，我放了链接）。

之后又进行了乘除法因式的等价无穷小代换（不清楚的，可以在最上面找，我放了链接）。

将【分析】整合到一起就是我上面放的答案

二、高阶无穷小运算法则?

真题考察：

答案如下：

三、等价无穷小的充分必要条件

由泰勒公式推导而来的几个等价无穷小代换公式的理论依据↑

四、泰勒公式及介绍

要想利用泰勒公式做题，甚至是考研真题（下面会讲解）。上面三个部分：和取低阶原则，高阶无穷小运算法则，等价无穷小的充分必要条件，大家需要了解清楚。

---

大家在零基础阶段只需记住公式，会做题。后面会讲到公式来源

泰勒公式如下：

x->0时，

下面挑第一个公式进行拓展了解：

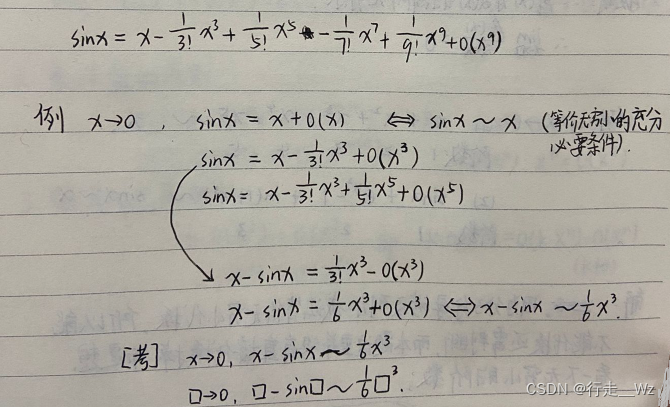
通过泰勒公式推出x - sinx ~ ，接下来看看真题的考法：

答案如下：

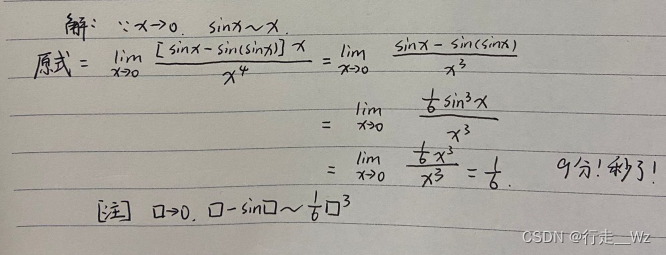
五、泰勒公式的用法（展开原则）

记住了公式只是第一步，怎么使用泰勒公式求函数极限才是关键

---

原则1：相消不为0原则

做两个题练一下泰勒公式展开：

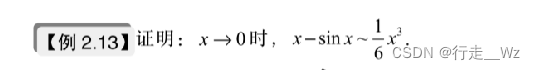
答案如下：

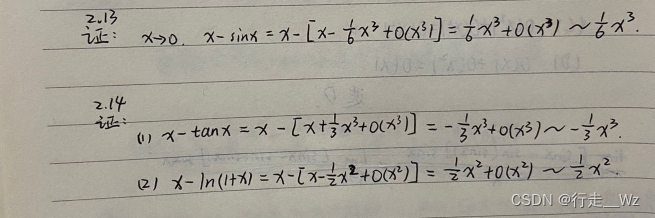
【考】补充5个重点等价无穷小公式（由泰勒公式推出）

由上面的证明题可以看出这几个公式是怎么得到的。

原则2：上下同阶原则（经验原则）

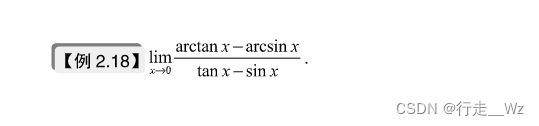
答案如下：

【分析】在泰勒公式原则1相消不为0已经知道tanx - sinx ~1/2，根据上下同阶原则，所以分子泰勒展开到三次方项。

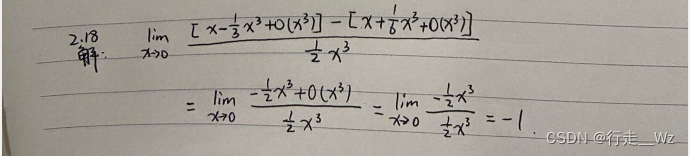
六、和取低阶原则易错点

本部分没写在第一部分和取低阶原则部分，是因为第一部分想让大家初步了解，如果一股脑儿都说了的话，可能会“劝退”大家，为了让大家“先完成，再完美”，所以放在最后进行说明。

---

解释：无穷小相加减，同阶数的式子放在一起进行利用等价无穷小看阶数是多少，比如本题，x与sinx都是1阶，放在一起看的话（x-sinx）~1/6，所以整体阶数是3，而ln(1+) ~?，阶数是2。"和取低阶原则"，留下ln(1+) ~?.

八、最后真题应用

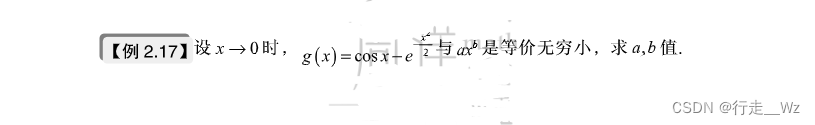
答案如下：

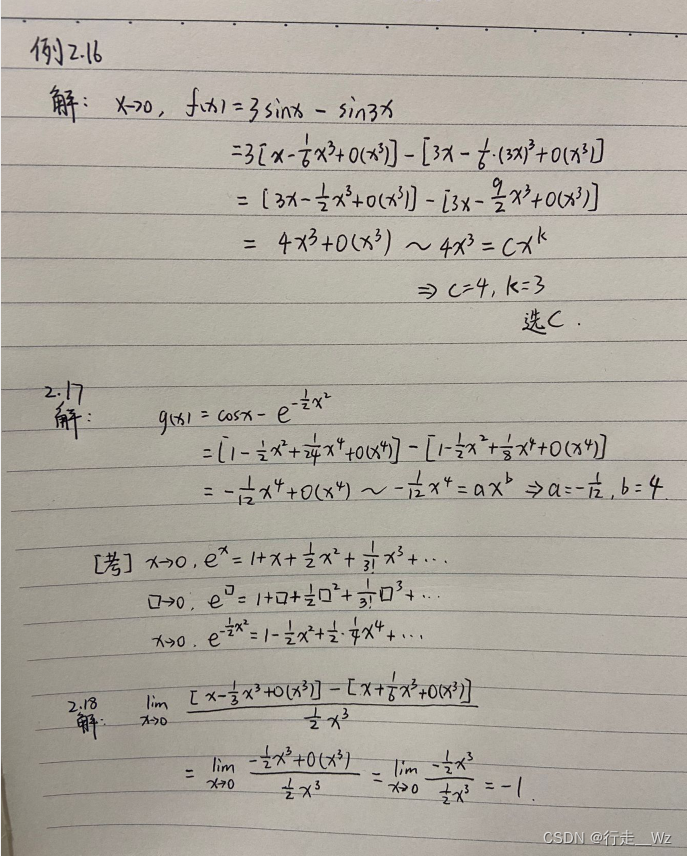
2012年真题解答：

如果上面对泰勒公式的讲解对大家有所帮助，荣幸之至！