Linux内核之红黑树详解（2）

该博客结合了维基百科、博客和一些其他的资料，按照理解整理的，如有错误，欢迎指正。

1、创建红黑树：

在实现插入、删除等操作之前，需要先创建一棵红黑树，返回的是红黑树的根结点：

RBRoot* create_rbtree()
{
    RBRoot *root = (RBRoot *)malloc(sizeof(RBRoot));
    root->node = NULL;
    return root;
}

2、插入：

在一棵红黑树中插入一个结点Z的步骤是：首先，将红黑树当作一棵二叉查找树，将结点插入树中；然后，将结点着色为红色（如果设置为黑色，就会造成根到叶子结点的路径上有一条路多一个额外的黑结点，这个很难调整，如果插入的是红色结点，可能会导致出现连续两个红色结点的冲突，可以通过颜色调换和树的旋转进行调整）；最后根据红黑树的性质来调整树的结构。红黑树的插入可能会出现5种情况，令将要插入的节点标为N，N的父节点标为P，N的祖父节点标为G，N的叔父节点标为U。我们分别进行分析：
将结点插入到红黑树中（把红黑树当作一棵二叉查找树，将结点添加到二叉查找树中）：

static void rbtree_insert(RBRoot *root, Node *node)
{
    Node *y = NULL;
    Node *x = root->node;
    while (x != NULL)// 将红黑树当作一颗二叉查找树，将节点添加到二叉查找树中。
    {
        y = x;
        if (node->key < x->key)
            x = x->left;
        else
            x = x->right;
    }
    ((y)->parent);
}

a、情况1：新结点位于树的根上，没有父节点。

这个可以分为两种情况：第一种情况是，新创建了一个红黑树，里面还没有数据，新插进的数据作为根结点；第二种情况是，红黑树中已经有了数据，但是在经过排序后，新插入的结点作为根结点。
第一种情况：

第二种情况：

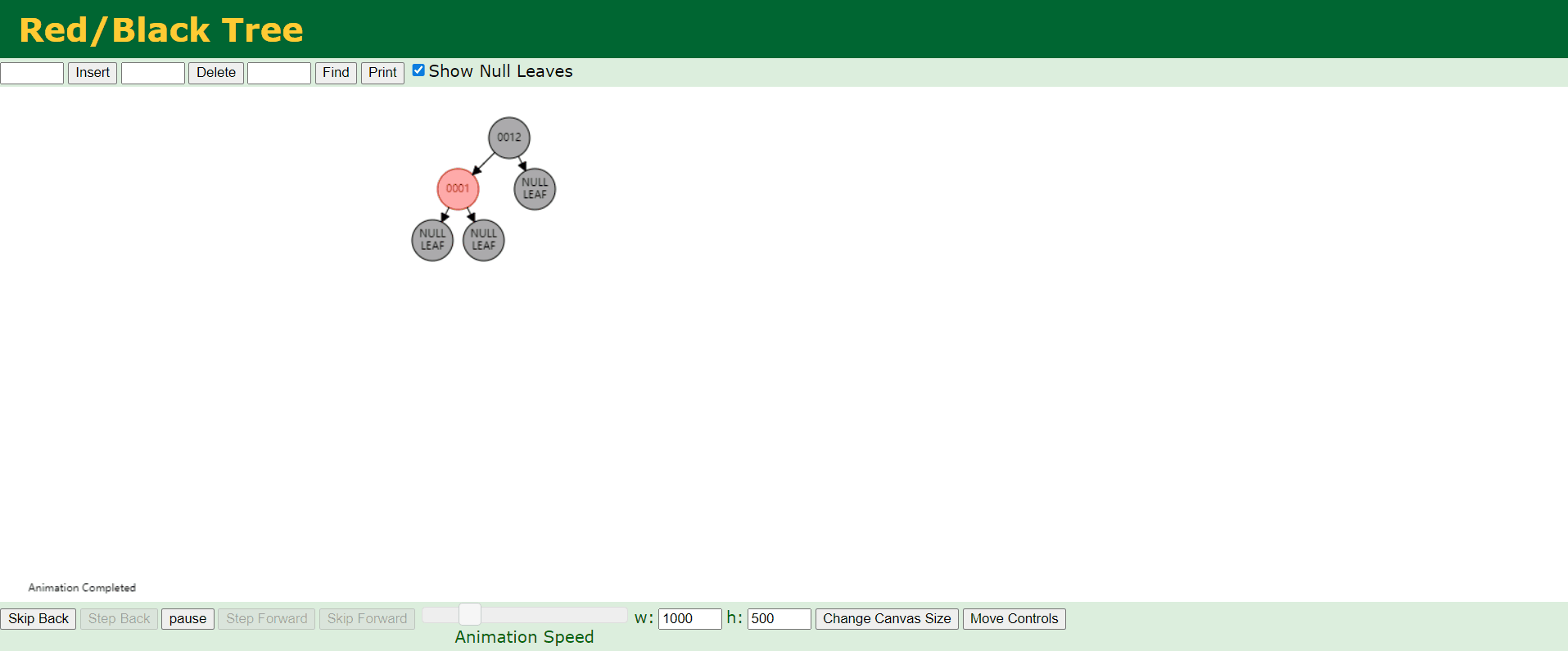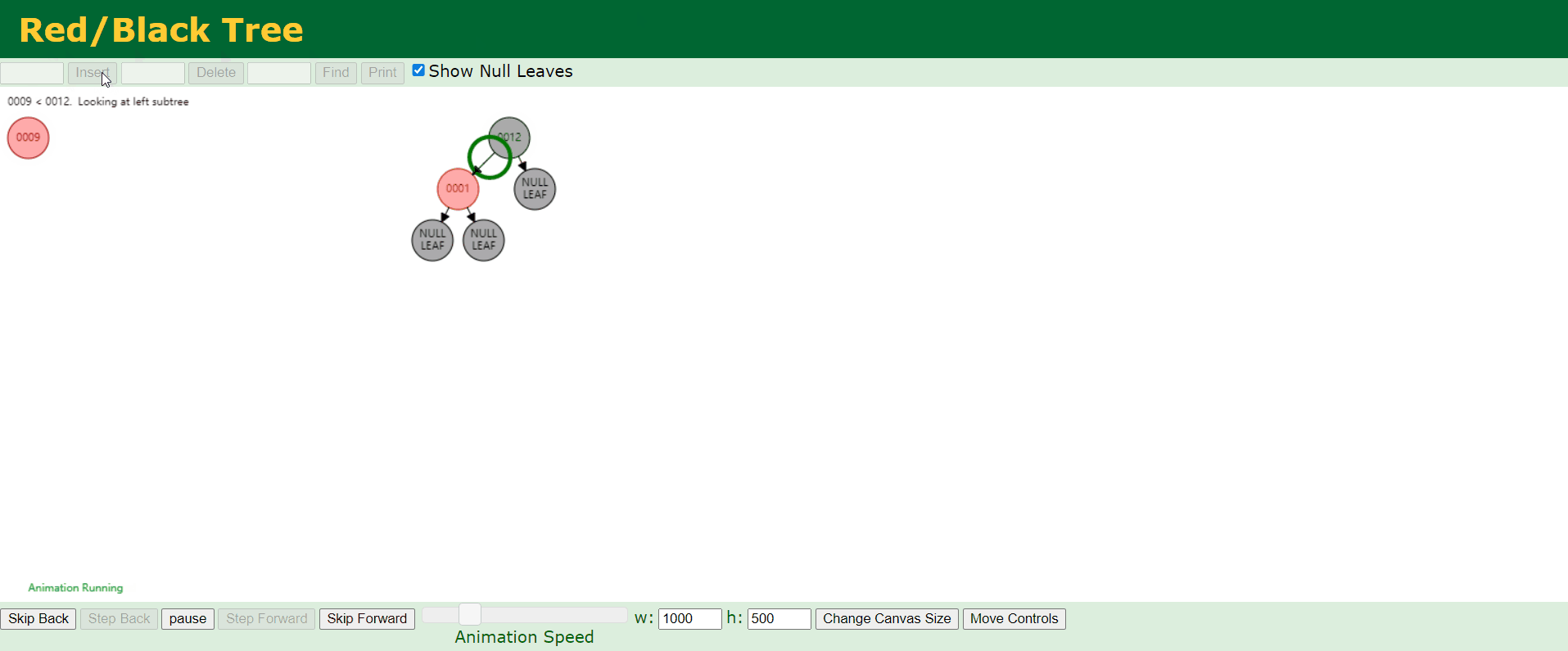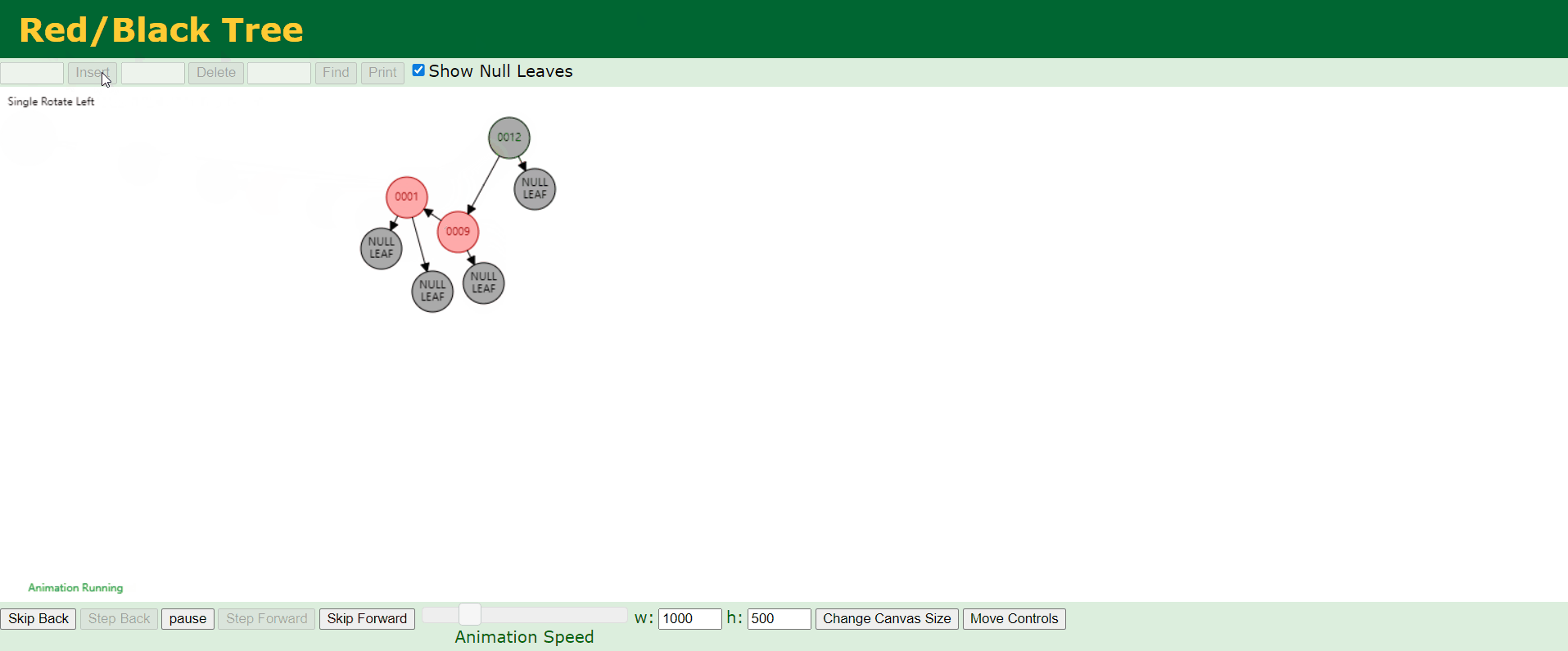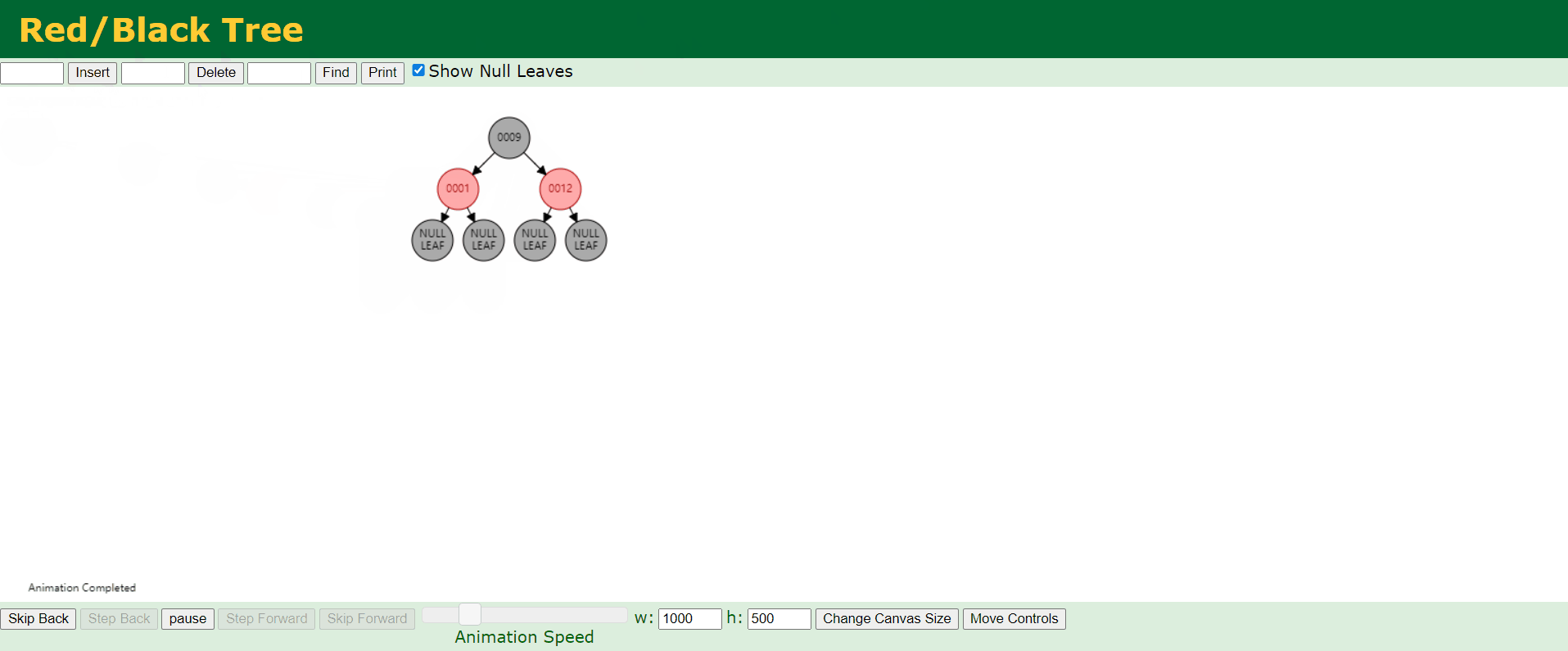
b、情况2：新结点的父结点P是黑色。

这种情况中，树仍然是有效的。虽然新结点N有两个黑色的叶子结点，但是新结点N是红色的，通过它的每个子结点的路径长度和未插入之前是相同的，所以仍满足红黑树的要求。

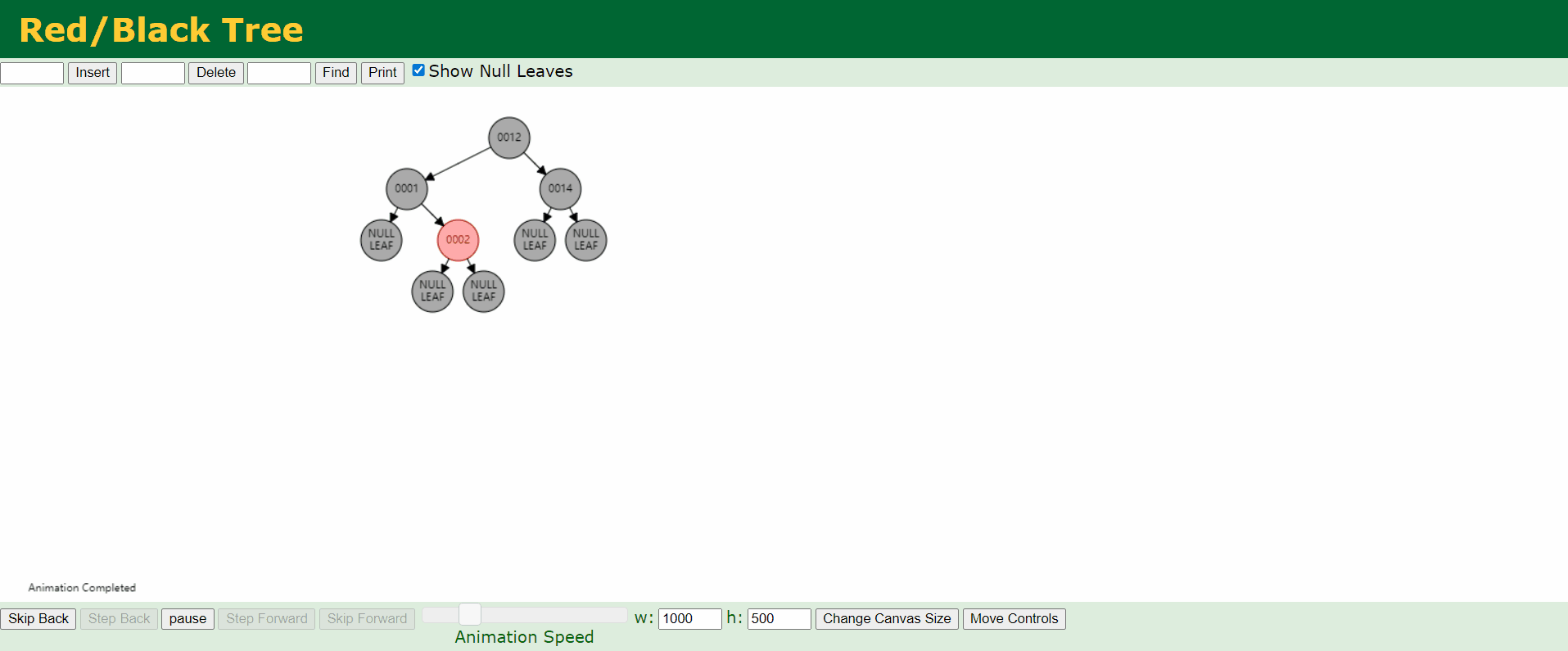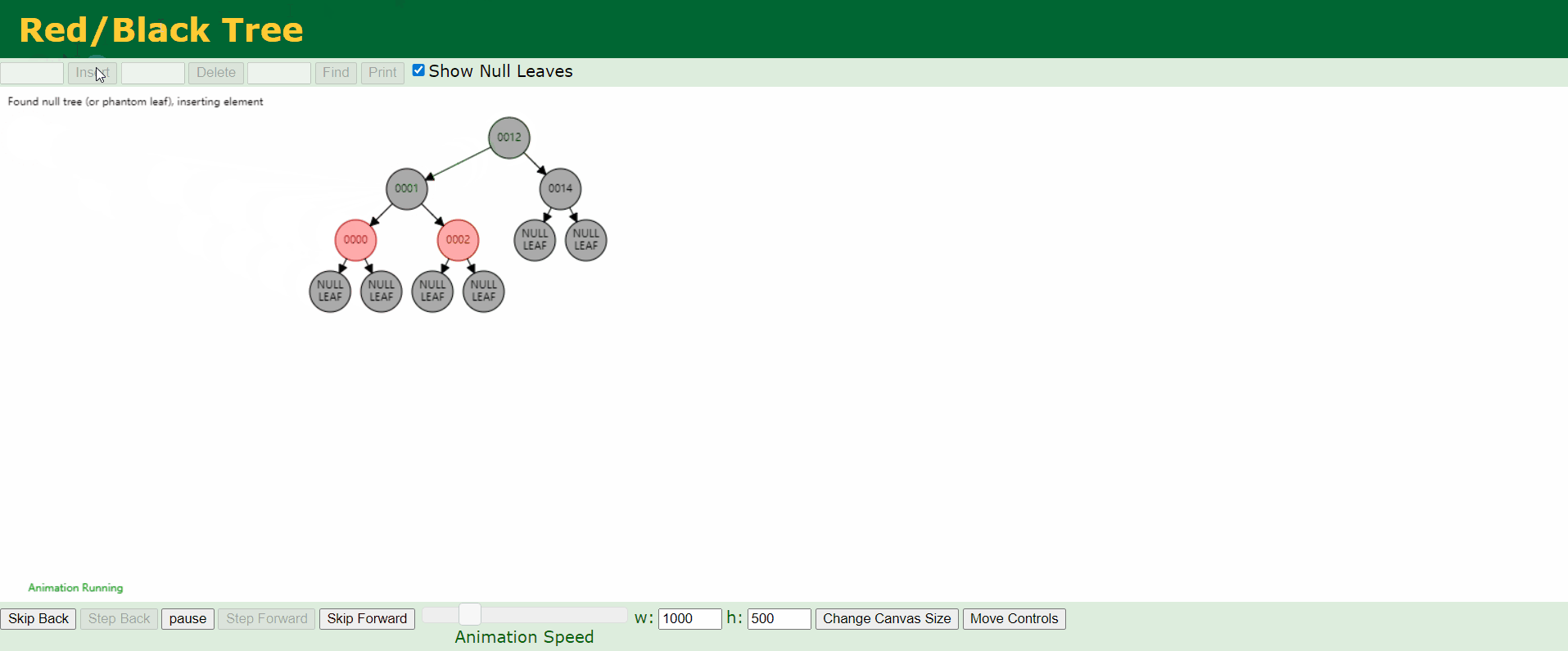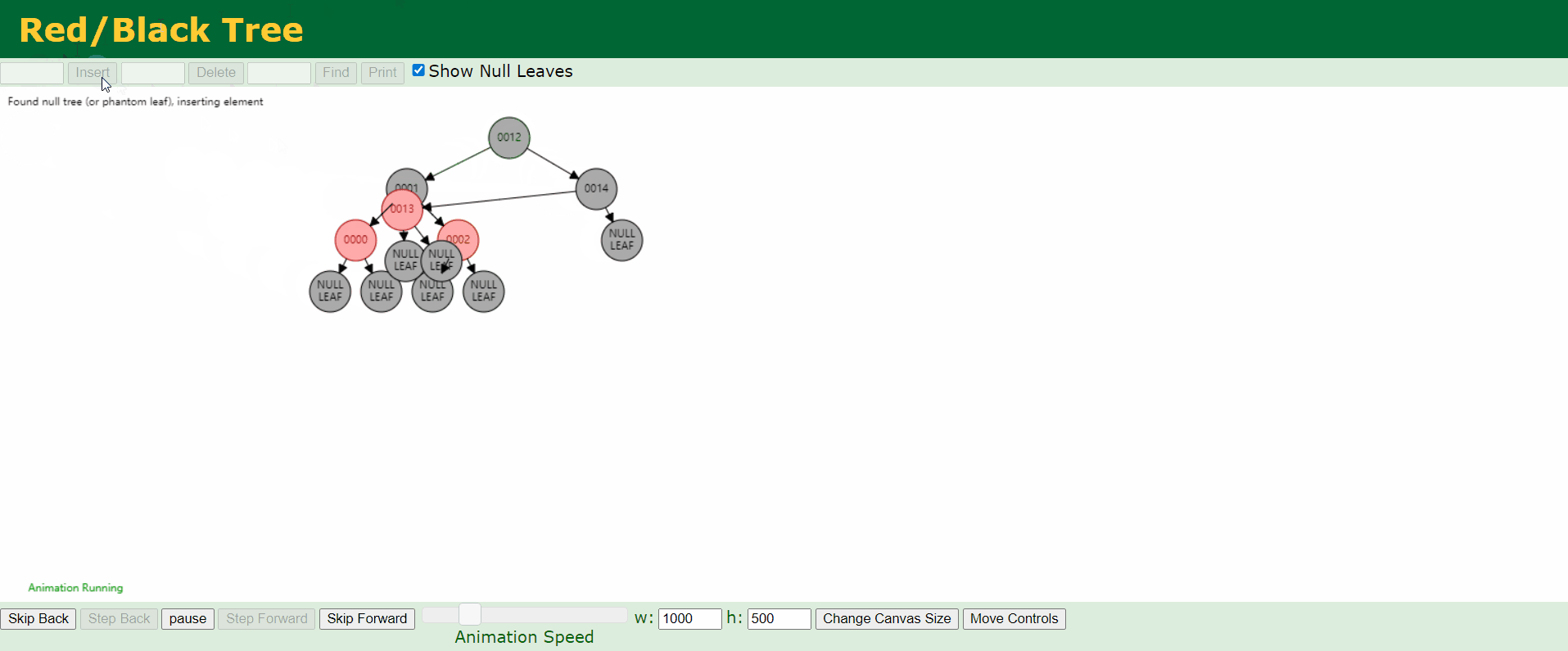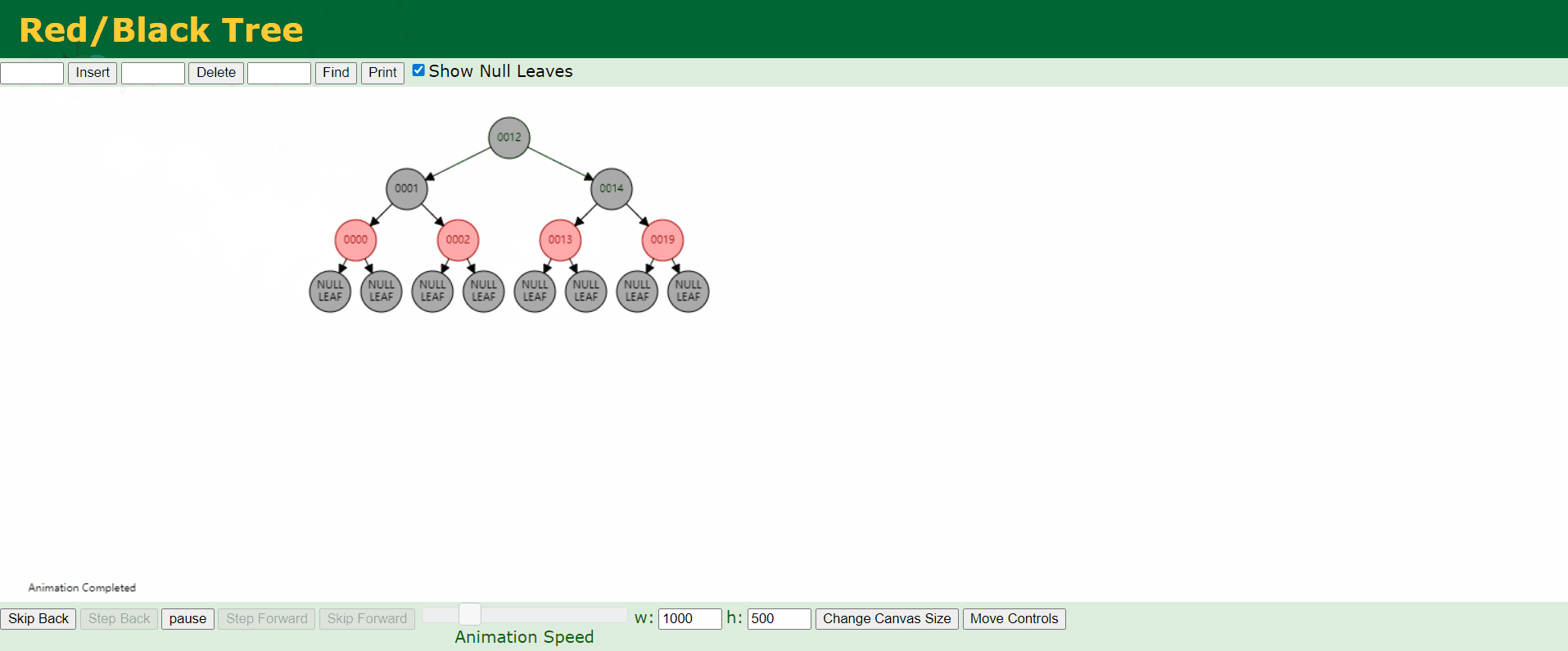
c、情况3：父结点P和叔结点U都是红色。

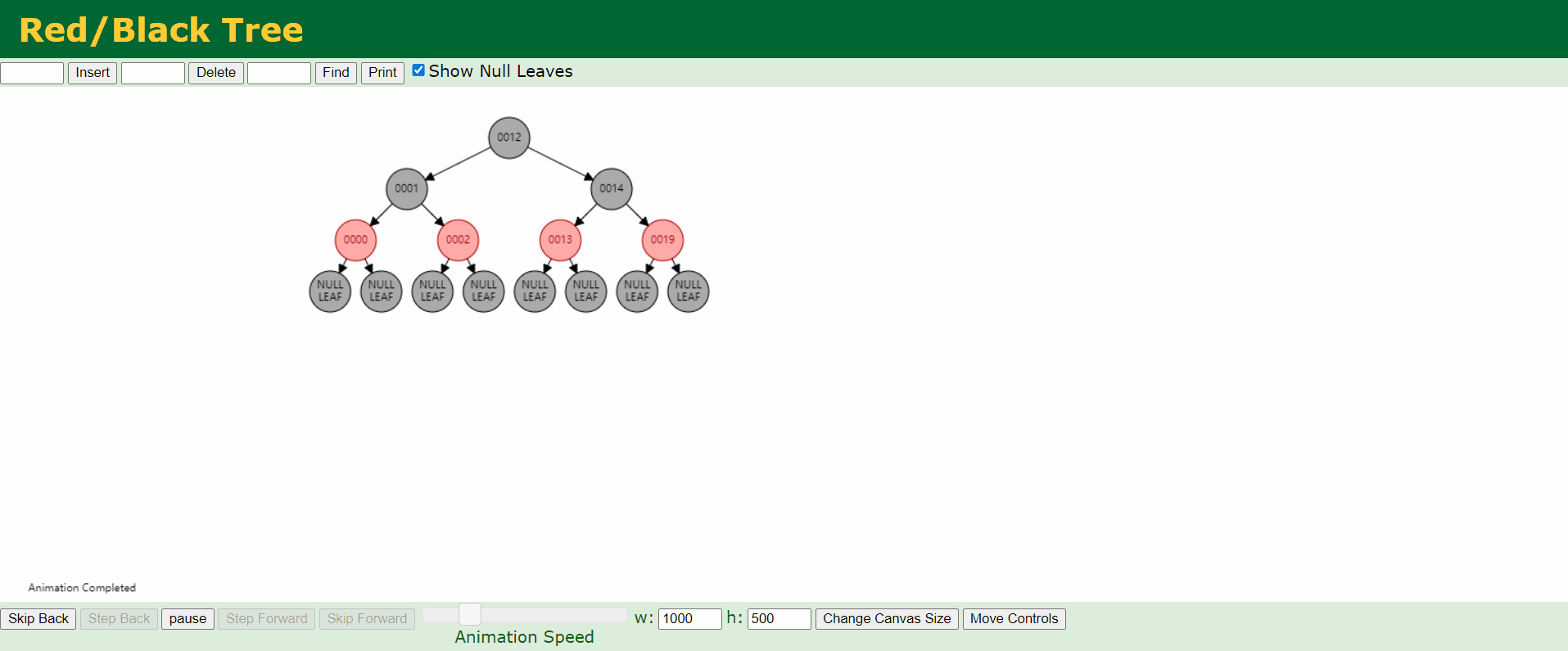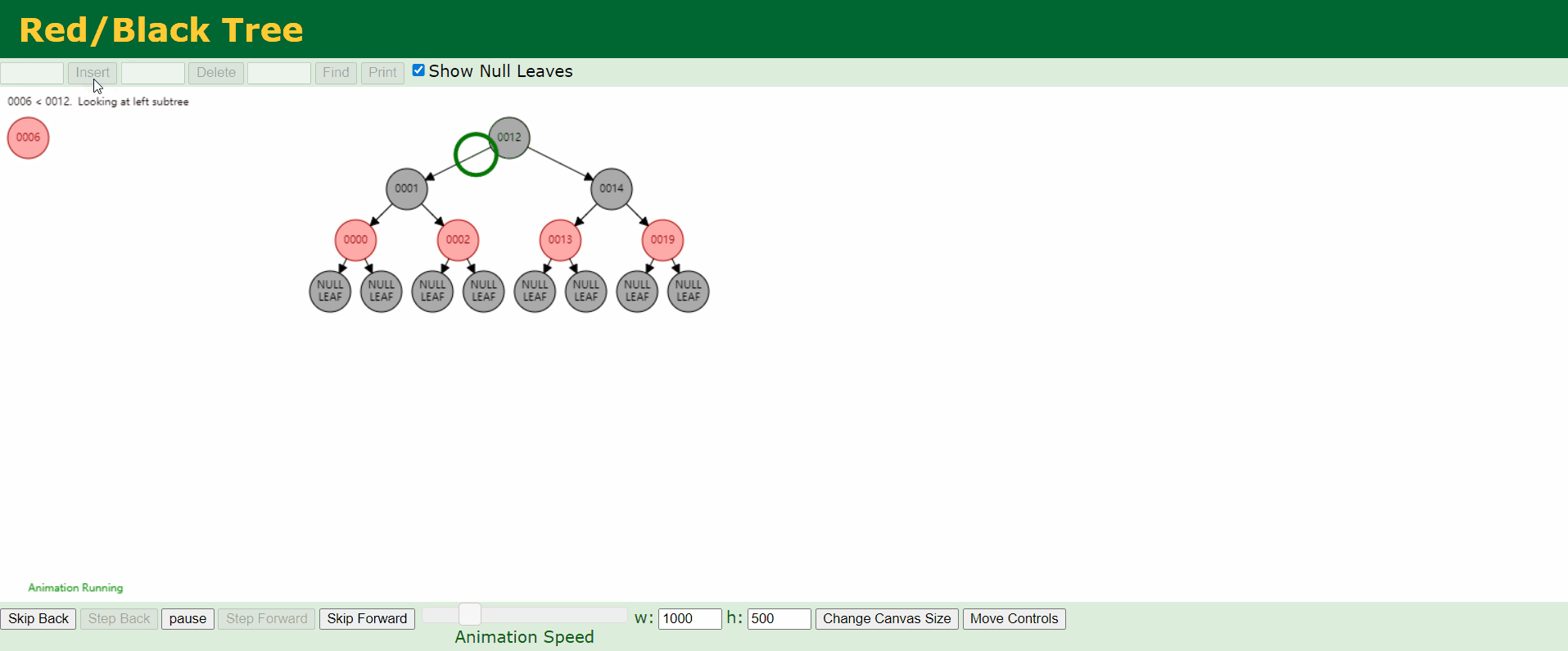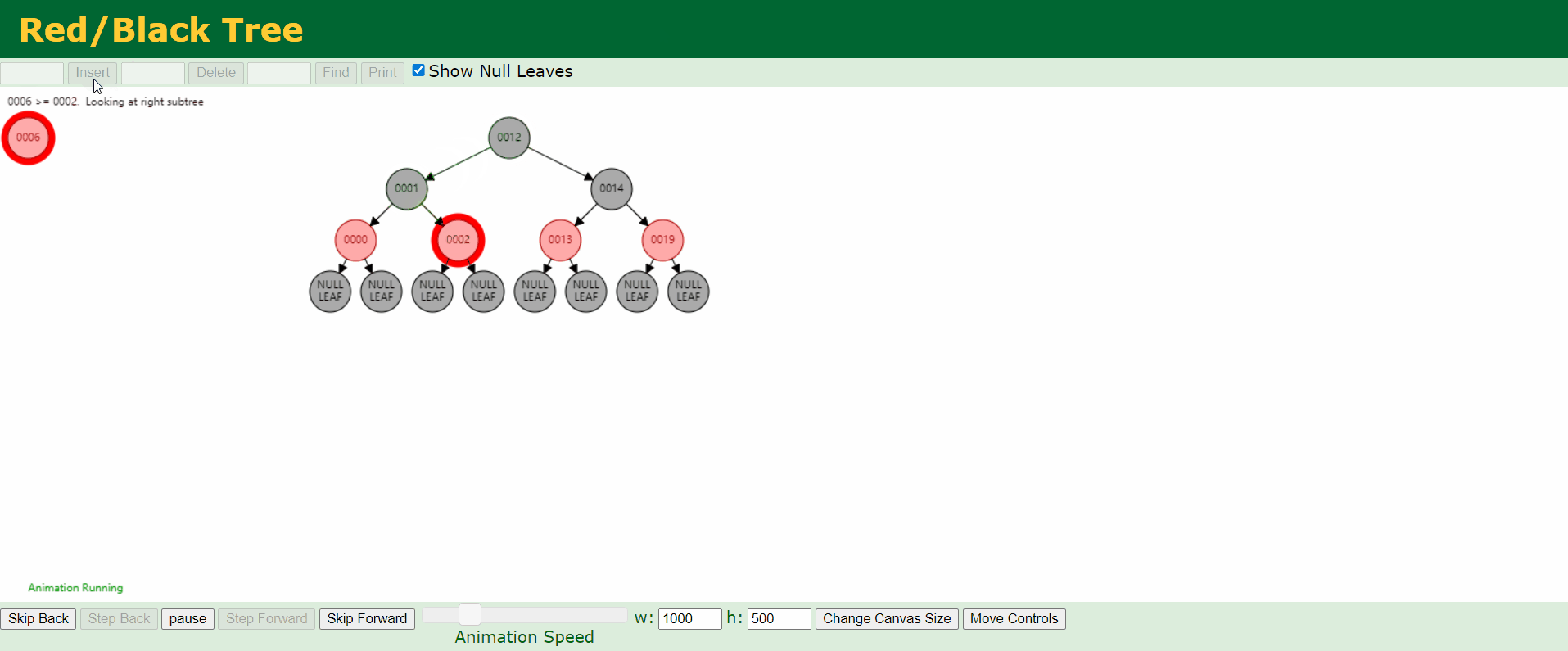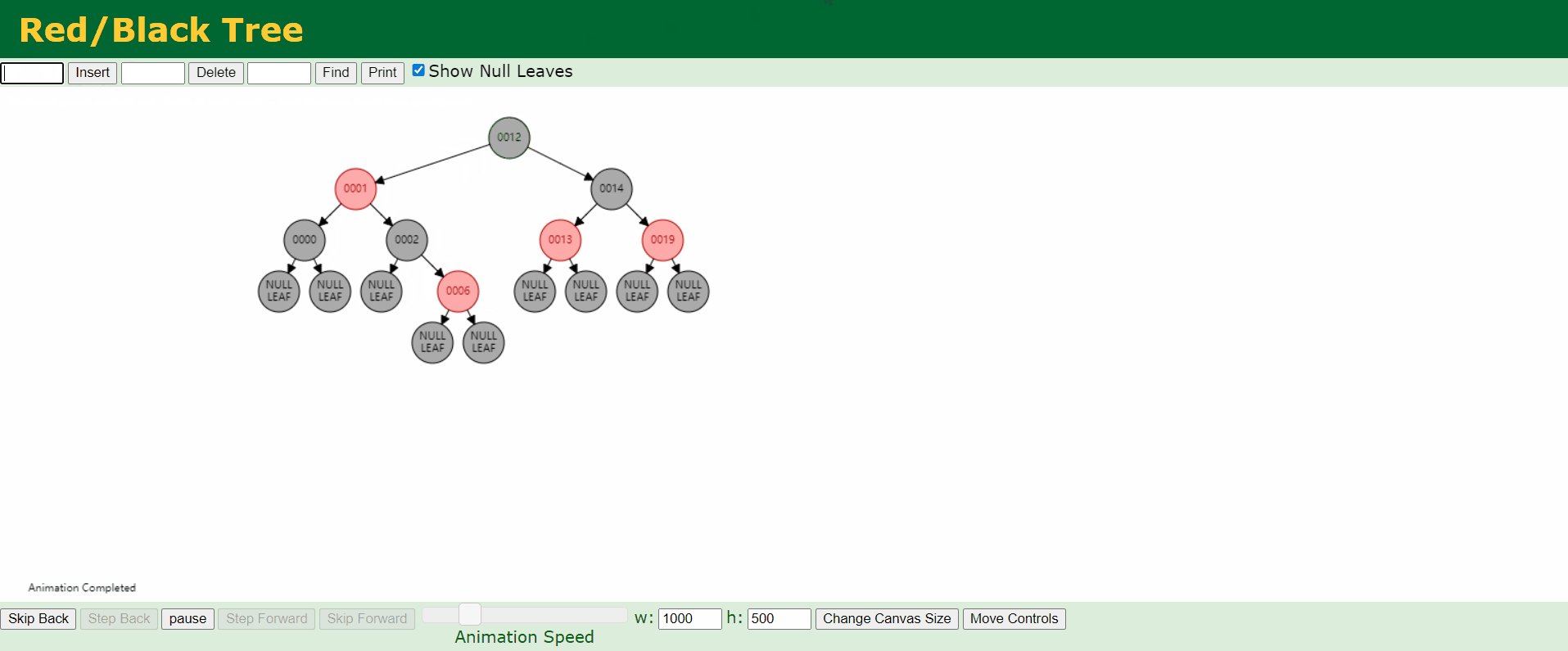
d、情况4：父结点P是红色，叔结点U是黑色或者缺少，且新结点N是父结点P的右结点而父结点P是祖父结点G的左结点。

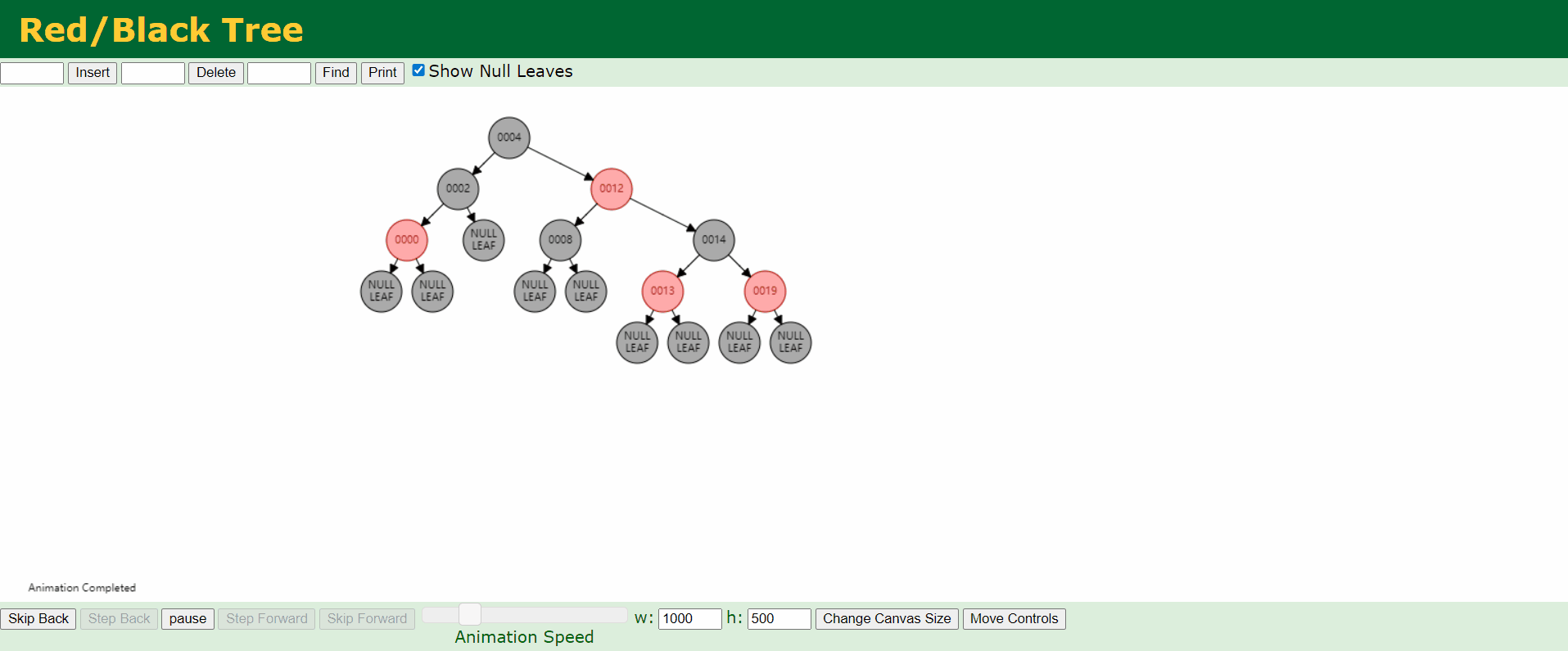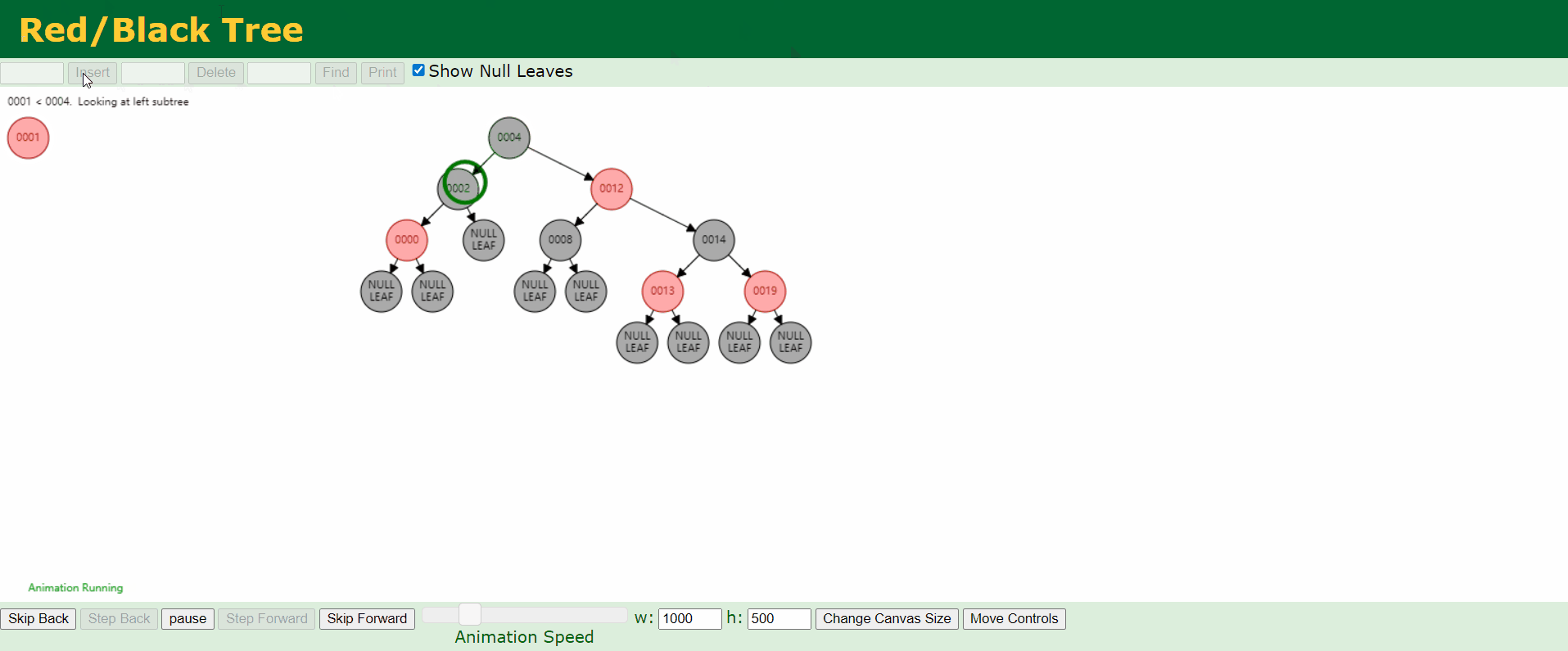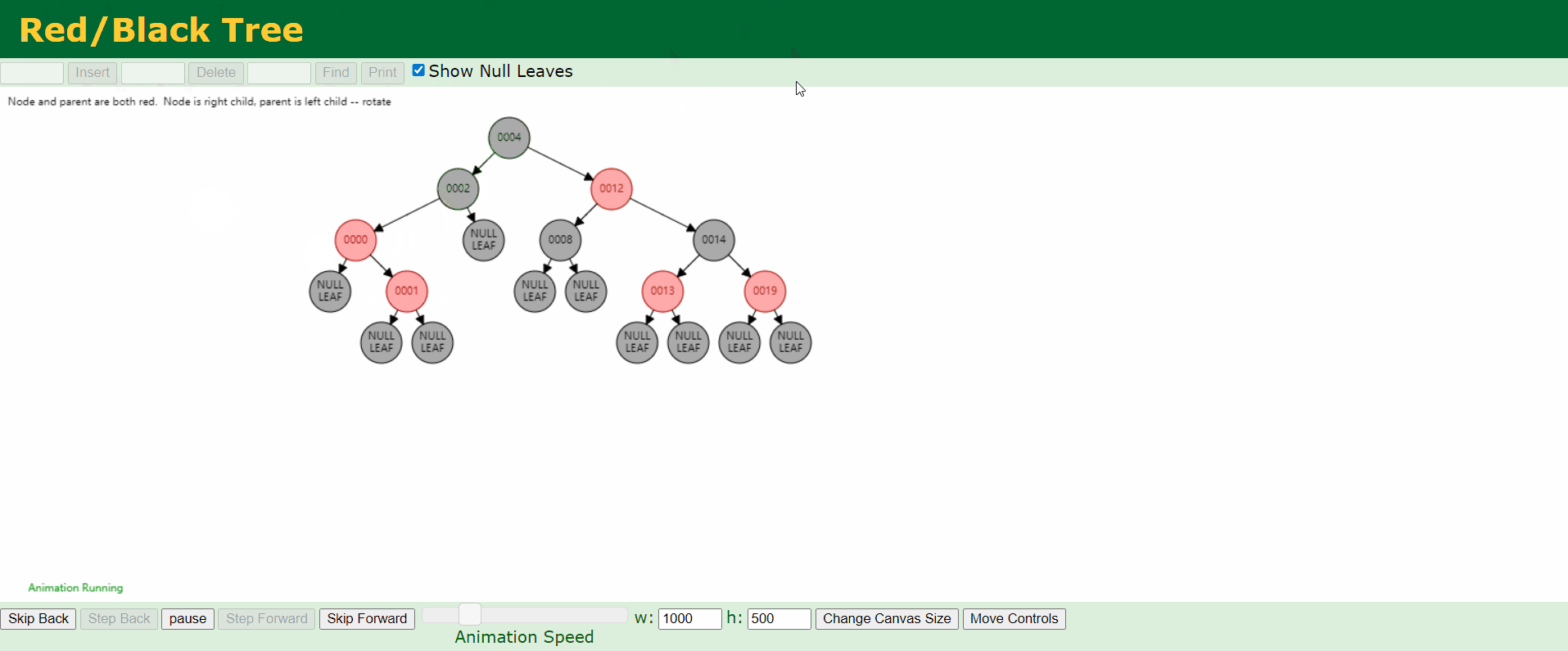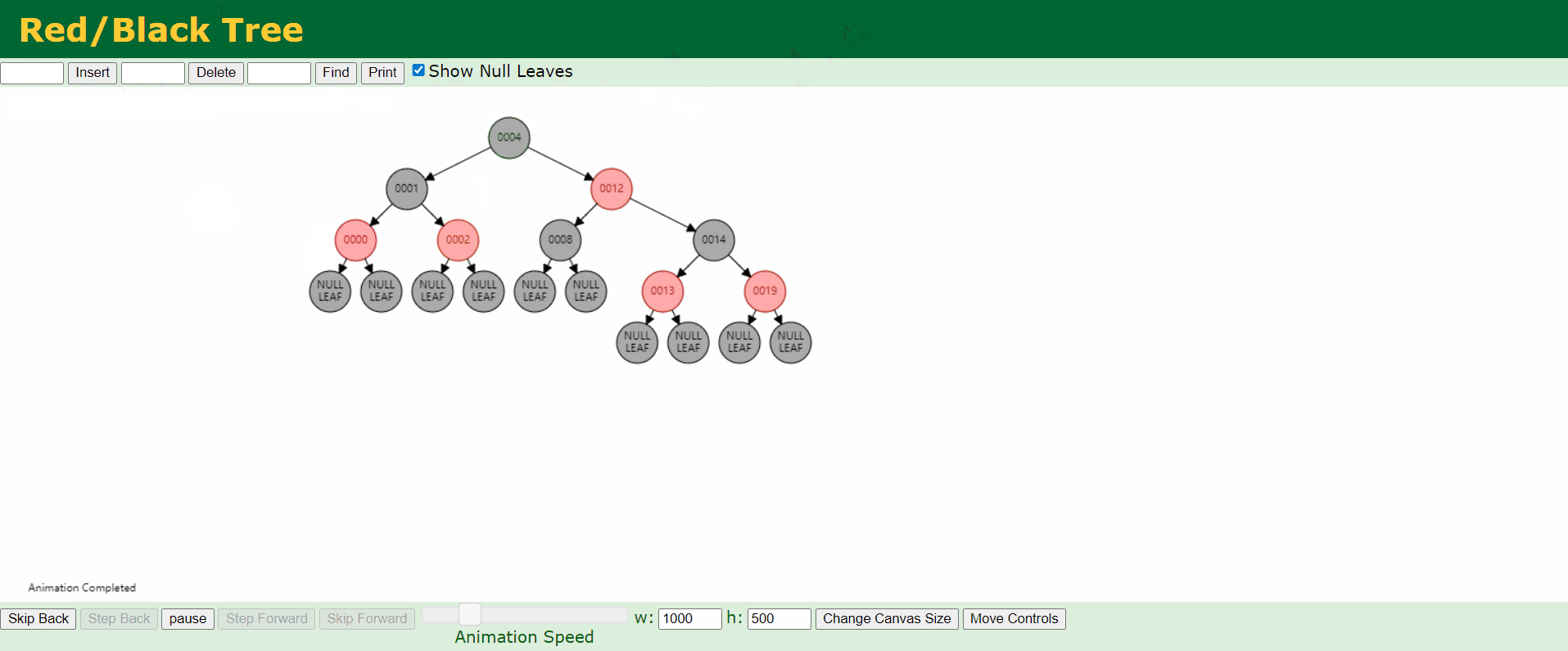
e、情况5：父结点P是红色，叔结点U是黑色或者缺少，且新结点N是父结点P的左结点而父结点P是祖父结点G的左结点。

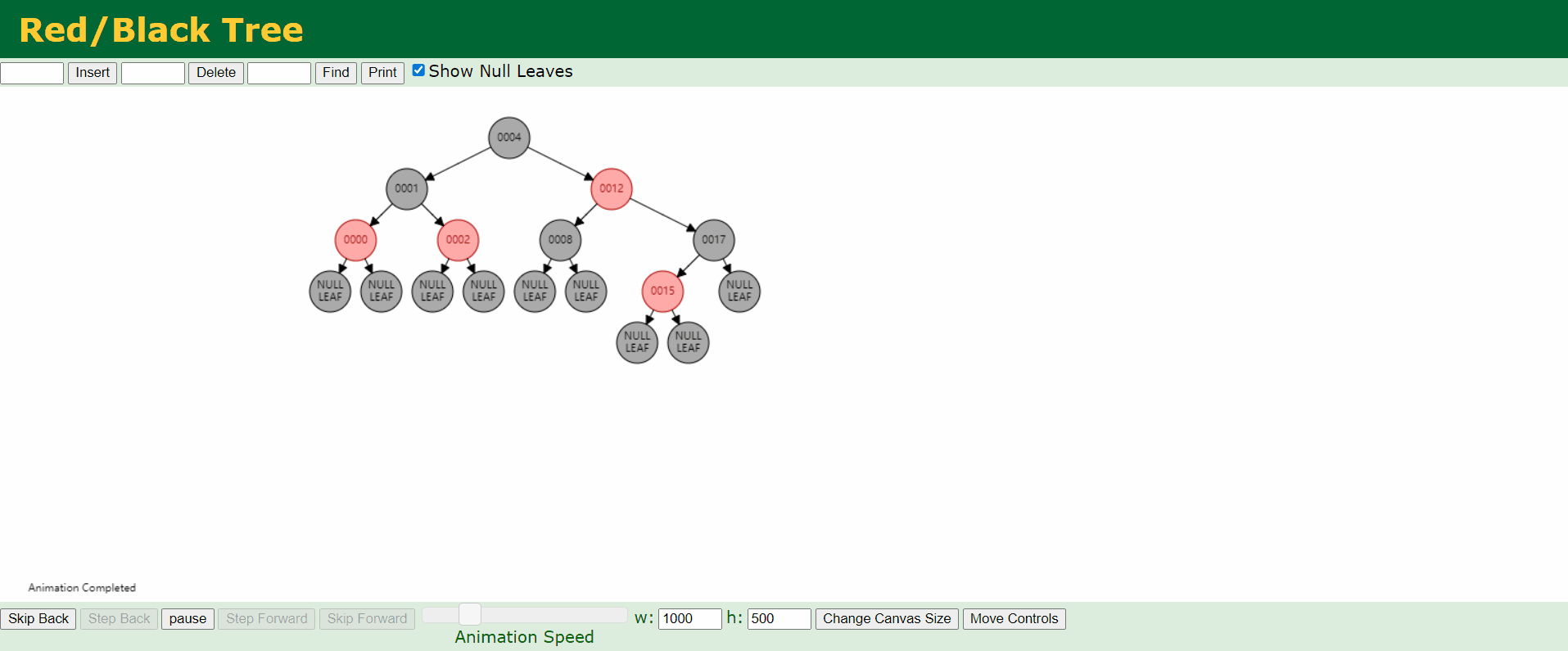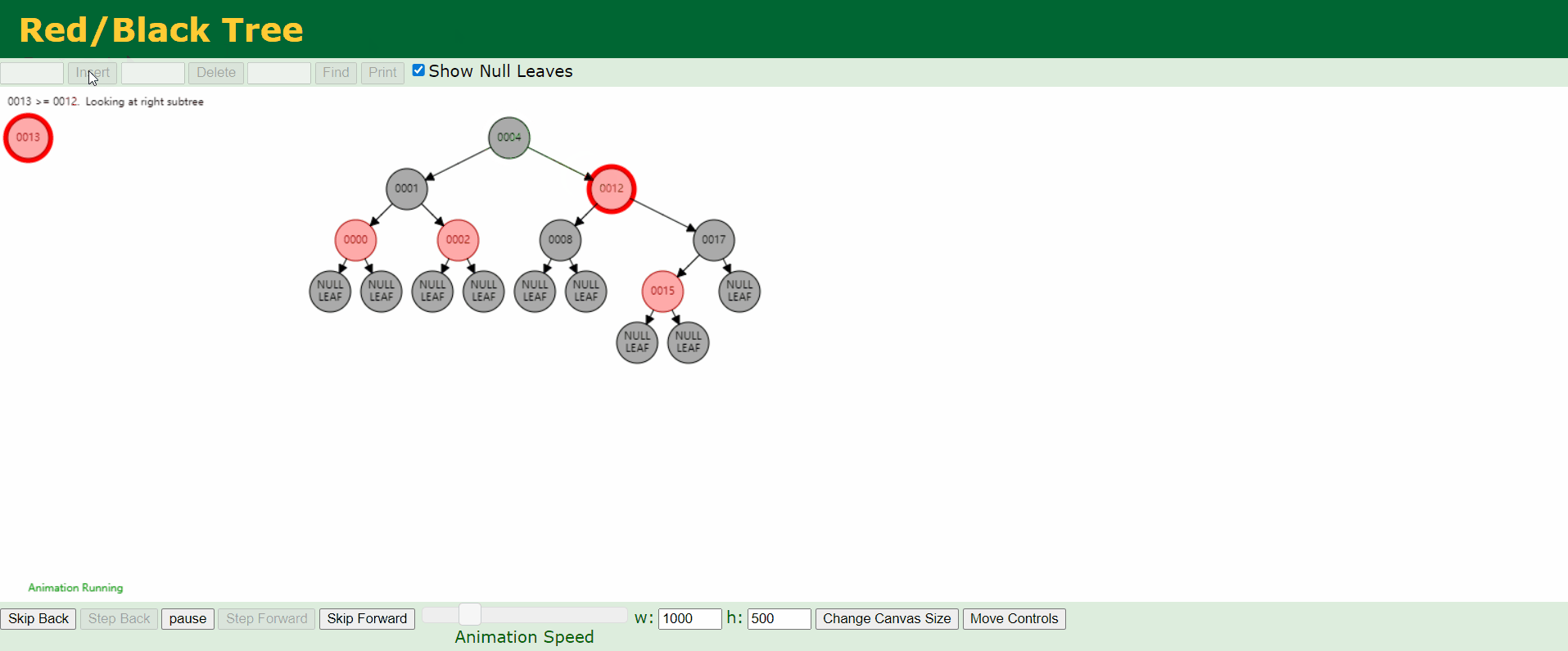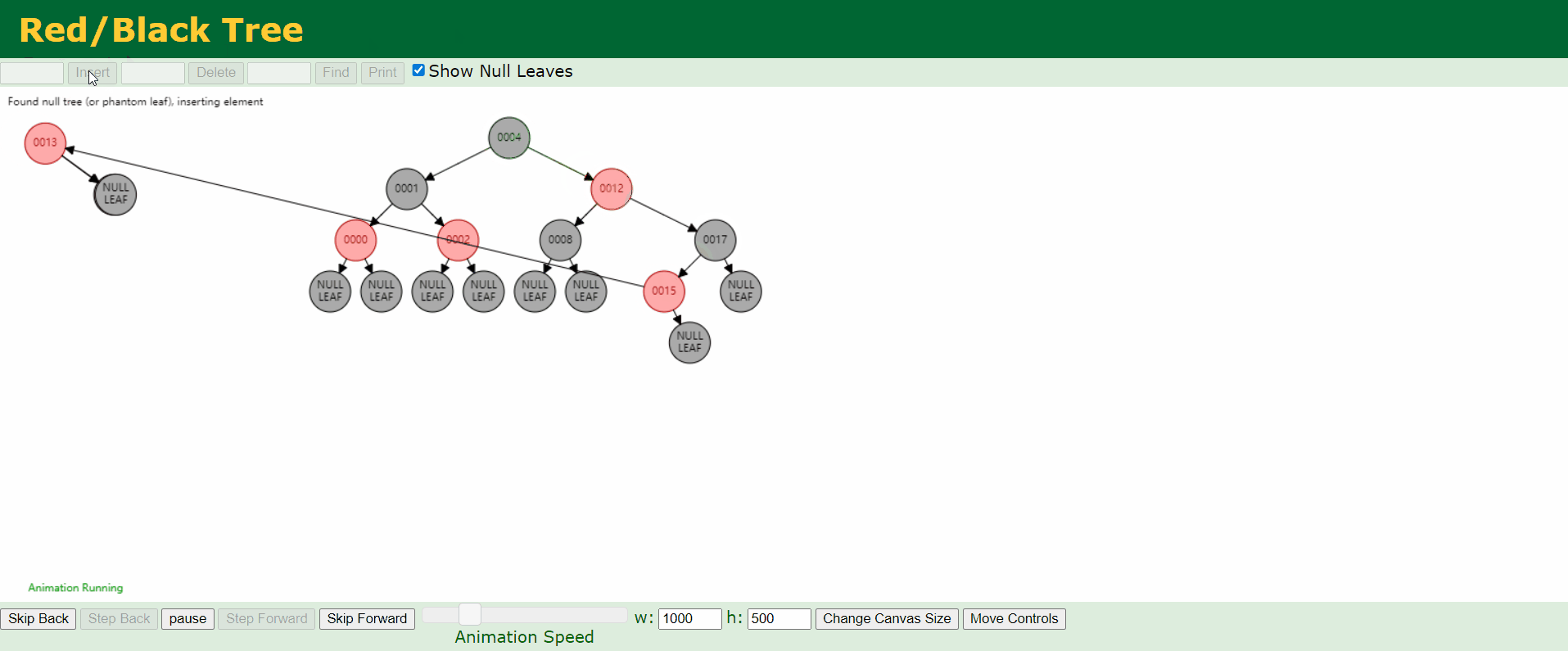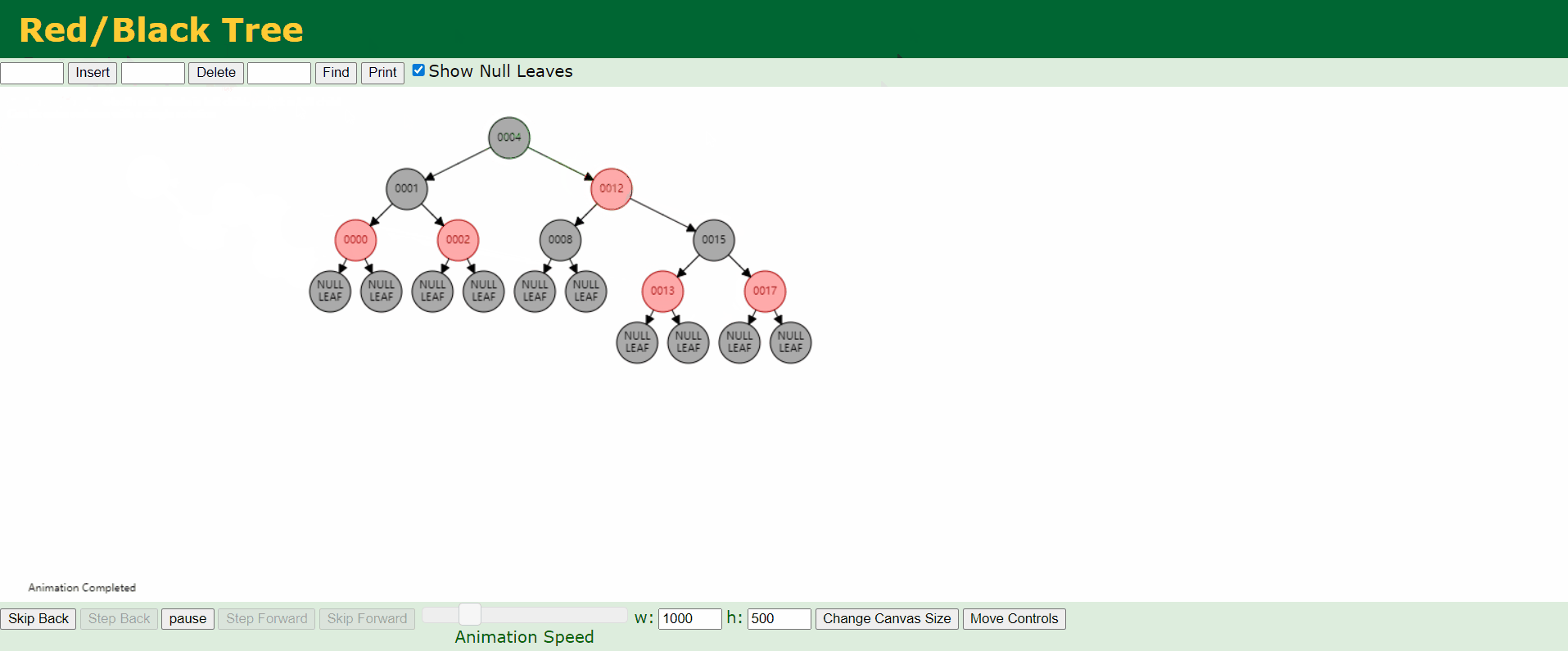
C语言实现：

/*
 * 红黑树插入修正函数
 *
 * 在向红黑树中插入节点之后(失去平衡)，再调用该函数；
 * 目的是将它重新塑造成一颗红黑树。
 *
 * 参数说明：
 *     root 红黑树的根
 *     node 插入的结点       
 */
static void rbtree_insert_fixup(RBRoot* root, Node* node)
{
    Node* parent, * gparent;

    // 若“父节点存在，并且父节点的颜色是红色”
    while ((parent = rb_parent(node)) && rb_is_red(parent))
    {
        gparent = rb_parent(parent);

        //若“父节点”是“祖父节点的左孩子”
        if (parent == gparent->left)
        {
            // Case 1条件：叔叔节点是红色
            {
                Node* uncle = gparent->right;
                if (uncle && rb_is_red(uncle))
                {
                    rb_set_black(uncle);
                    rb_set_black(parent);
                    rb_set_red(gparent);
                    node = gparent;
                    continue;
                }
            }

            // Case 2条件：叔叔是黑色，且当前节点是右孩子
            if (parent->right == node)
            {
                Node* tmp;
                rbtree_left_rotate(root, parent);
                tmp = parent;
                parent = node;
                node = tmp;
            }

            // Case 3条件：叔叔是黑色，且当前节点是左孩子。
            rb_set_black(parent);
            rb_set_red(gparent);
            rbtree_right_rotate(root, gparent);
        }
        else//若“z的父节点”是“z的祖父节点的右孩子”
        {
            // Case 1条件：叔叔节点是红色
            {
                Node* uncle = gparent->left;
                if (uncle && rb_is_red(uncle))
                {
                    rb_set_black(uncle);
                    rb_set_black(parent);
                    rb_set_red(gparent);
                    node = gparent;
                    continue;
                }
            }

            // Case 2条件：叔叔是黑色，且当前节点是左孩子
            if (parent->left == node)
            {
                Node* tmp;
                rbtree_right_rotate(root, parent);
                tmp = parent;
                parent = node;
                node = tmp;
            }

            // Case 3条件：叔叔是黑色，且当前节点是右孩子。
            rb_set_black(parent);
            rb_set_red(gparent);
            rbtree_left_rotate(root, gparent);
        }
    }

    // 将根节点设为黑色
    rb_set_black(root->node);
}

/*
 * 添加节点：将节点(node)插入到红黑树中
 *
 * 参数说明：
 *     root 红黑树的根
 *     node 插入的结点        
 */
static void rbtree_insert(RBRoot* root, Node* node)
{
    Node* y = NULL;
    Node* x = root->node;

    // 1. 将红黑树当作一颗二叉查找树，将节点添加到二叉查找树中。
    while (x != NULL)
    {
        y = x;
        if (node->key < x->key)
            x = x->left;
        else
            x = x->right;
    }
    rb_parent(node) = y;

    if (y != NULL)
    {
        if (node->key < y->key)
            y->left = node;                // 情况2：若“node所包含的值” < “y所包含的值”，则将node设为“y的左孩子”
        else
            y->right = node;            // 情况3：(“node所包含的值” >= “y所包含的值”)将node设为“y的右孩子”
    }
    else
    {
        root->node = node;                // 情况1：若y是空节点，则将node设为根
    }

    // 2. 设置节点的颜色为红色
    node->color = RED;

    // 3. 将它重新修正为一颗二叉查找树
    rbtree_insert_fixup(root, node);
}

/*
 * 创建结点
 *
 * 参数说明：
 *     key 是键值。
 *     parent 是父结点。
 *     left 是左孩子。
 *     right 是右孩子。
 */
static Node* create_rbtree_node(Type key, Node* parent, Node* left, Node* right)
{
    Node* p;

    if ((p = (Node*)malloc(sizeof(Node))) == NULL)
        return NULL;
    p->key = key;
    p->left = left;
    p->right = right;
    p->parent = parent;
    p->color = BLACK; // 默认为黑色

    return p;
}

/*
 * 新建结点(节点键值为key)，并将其插入到红黑树中
 *
 * 参数说明：
 *     root 红黑树的根
 *     key 插入结点的键值
 * 返回值：
 *     0，插入成功
 *     -1，插入失败
 */
int insert_rbtree(RBRoot* root, Type key)
{
    Node* node;    // 新建结点

    // 不允许插入相同键值的节点。
    // (若想允许插入相同键值的节点，注释掉下面两句话即可！)
    if (search(root->node, key) != NULL)
        return -1;

    // 如果新建结点失败，则返回。
    if ((node = create_rbtree_node(key, NULL, NULL, NULL)) == NULL)
        return -1;

    rbtree_insert(root, node);

    return 0;
}

代码参考地址：https://www.cnblogs.com/skywang12345/p/3624177.html