算法训练营Day22

#Java #回溯

开源学习资料

Feeling and experiences：

进入到回溯算法的章节，在代码随想录中有详细的回溯算法理论基础

在此总结归纳：

刚开始接触到回溯时，看到了终止条件，递归调用.....等，发现了其与递归三部曲有异曲同工之妙~

回溯三部曲：

1. 路径：
? 已经做出的选择，代表了到达当前状态所经过的路径。
? 通常表示为一个列表或栈，用来保存已经做出的选择。

2. 选择列表：
? 当前可以做的选择。
? 根据问题的不同，选择列表可能会随着路径的增长而变化。
? 重要的是要从选择列表中排除那些因为已经在路径中的选择而变得不合适的选项。

3. 结束条件：
? 何时停止递归，结束当前的探索过程。
? 通常是达到了问题的解决条件，如路径长度达到某个值，或是已经检查了所有可能的选择。

组合：力扣题目链接

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

你可以按 任何顺序 返回答案。

以下引用代码随想录中的图解：

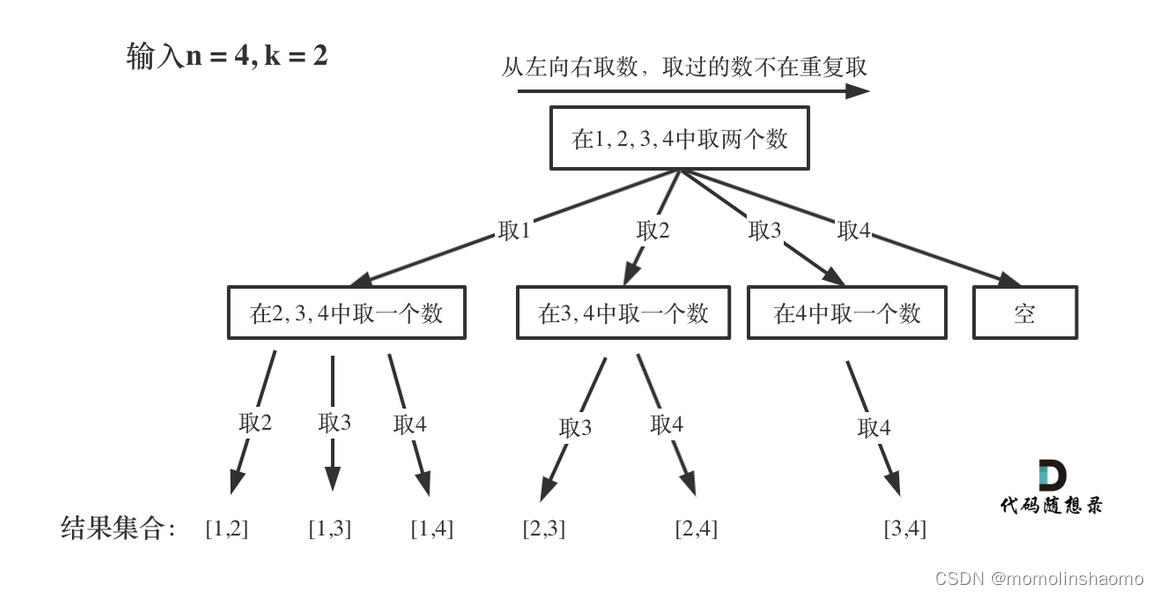
代码如下：

class Solution {
    //创建一个集合，用来存放每一次组合结果
     List<List<Integer>> ans = new ArrayList<>();
     //创建一个链式集合，用来进行回溯操作
     List<Integer> path = new LinkedList<>();
    public List<List<Integer>> combine(int n, int k) {
        getCombine(n,k,1);
        return ans;
    }


    public void getCombine(int n , int k , int startIndex){
         //终止条件:当path 的大小为 k 时则要返回一次结果
         if(path.size() == k){
             ans.add(new ArrayList(path));
             return;
         }
         for(int i = startIndex; i <=n;i++){
             path.add(i);
             getCombine(n,k,i+1);
             path.removeLast();
         }
    }
}

?整体思路：

? 终止条件：当path的大小等于k时，将其添加到ans中，并返回上一层递归。

? 循环和递归：从startIndex遍历到n。对于每个i，执行以下操作：
? 选择：将i加入path。
? 递归：调用getCombine(n,?k,?i?+?1)进行下一步的选择。
? 撤销选择：递归返回后，移除path的最后一个元素（这是撤销操作的核心）。

为什么在递归调用getCombine时，是 i+1，而不是 startIndex + 1 ？

? 如果使用startIndex+1，每次递归调用时起始索引只会基于原始的startIndex递增，而不是基于当前选择的数字 i 。
这将导致生成重复的组合。例如，对于(n,?k)?=?(4,?2)，使用startIndex+1可能会产生两次[1,?2]的组合：一次从1开始，一次从2开始。

? 使用i+1是为了在每次递归时，都是基于当前选择的数字进一步选择更大的数字，保证了组合中的数字是按照递增顺序排列的，同时避免了重复的组合。

对于剪枝优化，后面再做深入学习~

Fighting!