MIT_线性代数笔记:第 18 讲 行列式及其性质
课程进入第二大部分,之前学习了大量长方形矩阵的性质,现在我们集中讨论方阵的性质,行列式和特征值将我们的又一个重点,求行列式则与特征值息息相关。
行列式 Determinants
行列式是一个每个方阵都具有的数值,我们将矩阵 A 的行列式记作
d
e
t
(
A
)
=
∣
A
∣
det(A)= \begin{vmatrix} A \end{vmatrix}
det(A)=
?A?
?
它将尽可能多的矩阵信息压缩在这一个数里。例如矩阵不可逆或称奇异与矩阵的行列式等于 0 等价,因此可以用行列式来判定矩阵是否可逆。
性质 Properties
直接给出 n 阶行列式的公式,则一下子代入了大量信息,并不利于接受这个概念,我们从行列式的三个性质开始讲起,这三个性质定义了行列式。
这里可以给出二阶行列式的表达式
∣
a
b
c
d
∣
=
a
d
?
b
c
\begin{vmatrix} a \quad b \\ c \quad d \end{vmatrix} \quad = \begin{matrix} ad - bc \end{matrix}
?abcd?
?=ad?bc?
我们可以用它来验证行列式的性质,也可以看到它本身是可以从行列式的性质推导出来的。
- det(I)=1 。
∣ 1 0 0 1 ∣ = + 1 \begin{vmatrix} 1 \quad 0 \\ 0 \quad 1 \end{vmatrix} \quad = \begin{matrix} +1 \end{matrix} ?1001? ?=+1? - 如果交换行列式的两行,则行列式的数值会反号。从前两条可以推知置换矩阵的行列式是+1 或者-1。
∣ 0 1 1 0 ∣ = ? 1 \begin{vmatrix} 0 \quad 1 \\ 1 \quad 0 \end{vmatrix} \quad = \begin{matrix} -1 \end{matrix} ?0110? ?=?1? - (a)如果在矩阵的一行乘上 t,则行列式的值就要乘上 t。
(b)行列式是“矩阵的行”的线性函数。
∣ t a t b c d ∣ = t ∣ a b c d ∣ \begin{vmatrix} ta \quad tb \\ c \quad d \end{vmatrix} \quad = t \begin{vmatrix} a \quad b \\ c \quad d \end{vmatrix} ?tatbcd? ?=t ?abcd? ?
∣ a + a ′ b + b ′ c d ∣ = ∣ a b c d ∣ + ∣ a ′ b ′ c d ∣ \begin{vmatrix} a + a' \quad b + b' \\ c \quad d \end{vmatrix} \quad = \begin{vmatrix} a \quad b \\ c \quad d \end{vmatrix} +\begin{vmatrix} a' \quad b' \\ c \quad d \end{vmatrix} ?a+a′b+b′cd? ?= ?abcd? ?+ ?a′b′cd? ?
-
如果矩阵的两行是完全相同的,则它的行列式为 0。这可以从第二条性质推导出来,因为交换这个相同的两行,行列式应该变号;但是新生成的矩阵跟原矩阵没有区别,因此行列式应该不变,所以有 det = -det,所以 det 等于 0。
-
从矩阵的某行 k 减去另一行 i 的倍数,并不改变行列式的数值,我们以二阶为
例:

-
如矩阵 A 的某一行都是 0,则其行列式为 0。可以应用性质 3(a),取 t=0 证明。
-
三角阵的行列式的值等于其对角线上数值(主元)的乘积。
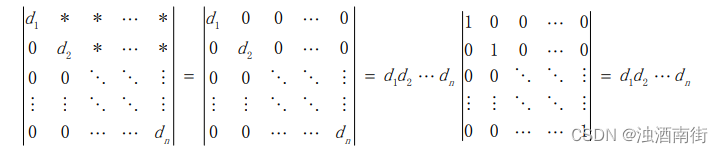
性质 5 告诉我们三角阵通过行消元法得到对角阵的过程中,行列式的数值没有发生变化。性质 3(a)告诉我们对角阵的行列式等于其主元的乘积再乘以单位阵的行列式。而性质 1 表明单位阵行列式为 1。 -
当且仅当矩阵 A 为奇异矩阵时,其行列式为 0。 如果矩阵 A 为奇异阵,则必可通过消元法使得矩阵的某行全等于零,则按照性
质 6,A 的行列式为 0。 如果其不是奇异阵,则通过消元可以得到一个上三角矩阵,且其主元均不为 0,则按照性质 7,行列式的数值等于主元的乘积也不等于 0。
计算非奇异矩阵的行列式有确切的公式,但通常计算机是靠消元的方法来转化为三角阵,然后将主元相乘来进行计算的。
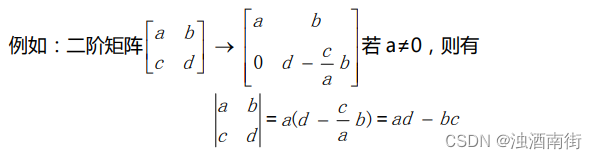
-
det(AB)=det(A)det(B)
尽管矩阵的和的行列式不等于行列式的和,但矩阵乘积的行列式等于矩阵行列
式的乘积。
如果 A 为可逆矩阵,则 A ? 1 A^{-1} A?1 A=I,所以有
d e t ( A ? 1 ) = 1 d e t ( A ) det(A^{-1}) =\frac {1}{det(A)} det(A?1)=det(A)1?
此外,det( A 2 A^2 A2)= d e t ( A ) 2 det(A)^2 det(A)2 并且有 det(2A)= 2 n 2^n 2ndet(A)。后一个公式让我们容易联想到体积,当长宽高都倍增之后,体积变成了原来的 2 3 2^3 23=8 倍。 -
det( A T A^T AT)=det(A)
证明: 矩阵消元可得A=LU,则 A T A^T AT= U T U^T UT L T L^T LT,由性质9可知det(A)=det(L)det(U),
det( A T A^T AT)= det( L T L^T LT)det( U T U^T UT),根据性质 7 可知 det( L T L^T LT)=det(L),det( U T U^T UT)=det(U)
则二者乘积相等。
因为性质 10 成立,所以性质 2,3,4,5,6 可以用在行列式的列性质上。 行列式的性质 2 中隐藏着一个内容,这就是置换隐藏着奇偶性,一个矩阵不可能经过奇数次置换得到和偶数次置换相同的方阵。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Python双端队列的3种实现及应用
- 德州仪器(TI):市场形势仍不明朗
- 【Python 元编程】自定义上下文管理器入门指南 ?
- cpp面向对象的又一個重要特性, 多态(polymorphism)的vptr指针调用实现,以及为什么int**到了64位系统就会失效
- VCG 网格面片法向量平滑
- 迅为RK3568开发板助力智能车载产业快速发展
- 基于ChatGPT4+Python近红外光谱数据分析及机器学习与深度学习建模
- Blazor项目如何调用js文件
- Python猜数游戏
- Ubuntu使用手册