day20 最大的二叉树 合并二叉树 二叉搜索树中的搜索 验证二叉搜索树

题目1：654 最大二叉树

题目链接：654 最大二叉树

题意

根据不重复的整数数组nums构建最大的二叉树 ，根节点是数组中的最大值，最大值左边的子数组构建左子树，最大值右边的子数组构建右子树

nums数组中最少含有1个元素，并且nums中的元素数值均大于等于0

递归?

递归三部曲：

1）确定递归函数的参数和返回值

2）确定终止条件

3）确定单层递归逻辑

数组

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
       //终止条件  因为递归的时候左数组可能为空，右数组可能为空
       if(nums.size()==0) return NULL;
       //单层递归逻辑
       //寻找中节点
       //找寻切割数组的位置
       int maxvalue = 0;
       int index = 0;
       for(int i=0;i<nums.size();i++){
           if(nums[i]>maxvalue){
               maxvalue = nums[i];
               index = i;
           }
       }
       int rootvalue = maxvalue;
       TreeNode* root = new TreeNode(rootvalue);
       //叶子节点
       if(nums.size()==1) return root;
       //切割数组 左闭右开
       vector<int> leftnums(nums.begin(),nums.begin()+index);
       vector<int> rightnums(nums.begin()+index+1,nums.end());
       root->left = constructMaximumBinaryTree(leftnums);
       root->right = constructMaximumBinaryTree(rightnums);
       return root;
    }
};

下标

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* traversal(vector<int>& nums,int left,int right){
        //终止条件
        if(left>=right) return NULL;
        //单层递归逻辑
        //中节点
        int maxvalue = 0;
        int index = left;
        for(int i=left;i<right;i++){
            if(nums[i]>maxvalue){
                maxvalue = nums[i];
                index = i;
            }
        }
        TreeNode* root = new TreeNode(maxvalue);
        if(right - left == 1) return root;
        //左闭右开
        root->left = traversal(nums, left, index);
        //左闭右开
        root->right = traversal(nums, index+1, right);
        return root;
    }
    TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
        return traversal(nums,0,nums.size());
    }
};

题目2：617 合并二叉树

题目链接：617 合并二叉树

题意

两棵树相同位置的节点视为重叠，如果两棵树的两个节点重叠，将这两个节点的值相加作为新节点的值，若不重叠，则将不是NULL的节点作为新的节点，从而合成一颗新二叉树。

同时遍历两颗树的相同位置

递归

递归三部曲：

1）确定递归函数的参数和返回值

2）确定终止条件

3）确定单层递归逻辑

代码（返回改变后的root1）

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
        //终止条件
       if(root1==NULL) return root2;
       if(root2==NULL) return root1;
       //单层递归逻辑
       root1->val += root2->val;//中
       root1->left = mergeTrees(root1->left,root2->left);//左
       root1->right = mergeTrees(root1->right,root2->right);//右
       return root1;
    }
};

代码（新root）

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
        //终止条件
       if(root1==NULL) return root2;
       if(root2==NULL) return root1;
       //单层递归逻辑
       TreeNode* root = new TreeNode(0);
       root->val = root1->val += root2->val;//中
       root->left = mergeTrees(root1->left,root2->left);//左
       root->right = mergeTrees(root1->right,root2->right);//右
       return root;
    }
};

层序遍历

注意开始写 遇到NULL时的return 的情况

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
        queue<TreeNode*> que;
        //这里不应该这么写，可能root1==NULL root2!=NULL 这时应该返回root2
        // if(root1!=NULL) que.push(root1);
        // if(root2!=NULL) que.push(root2);
        if(root1==NULL) return root2;
        if(root2==NULL) return root1;
        que.push(root1);
        que.push(root2);
        while(!que.empty()){
            TreeNode* node1 = que.front();
            que.pop();
            TreeNode* node2 = que.front();
            que.pop();
            node1->val += node2->val;
            if(node1->left!=NULL && node2->left!=NULL){
                que.push(node1->left);
                que.push(node2->left);
            }
            if(node1->right!=NULL && node2->right!=NULL){
                que.push(node1->right);
                que.push(node2->right);
            }
            if(node1->left==NULL && node2->left!=NULL) node1->left = node2->left;
            if(node1->right==NULL && node2->right!=NULL) node1->right = node2->right;
        }
        return root1;
    }
};

题目3：700 二叉搜索树中的搜索

题目链接：700 二叉搜索树中的搜索

题意

在二叉搜索树中找到等值于val的节点，返回以该节点为根的子树，若不存在，则返回NULL

注意：二叉搜索树是有序的（左子树的值小于中节点的值，右子树的值均大于中节点的值），遍历二叉树，如果节点值小于val，说明要去该节点的右子树寻找；如果节点值大于val，说明要去该节点的的左子树寻找，如此递归下去

递归

递归三部曲

1）确定递归函数的返回值和参数

2）确定终止条件

3）确定单层递归逻辑? 按照二叉搜索树的特性作为顺序去遍历，不用考虑前序，中序和后序了

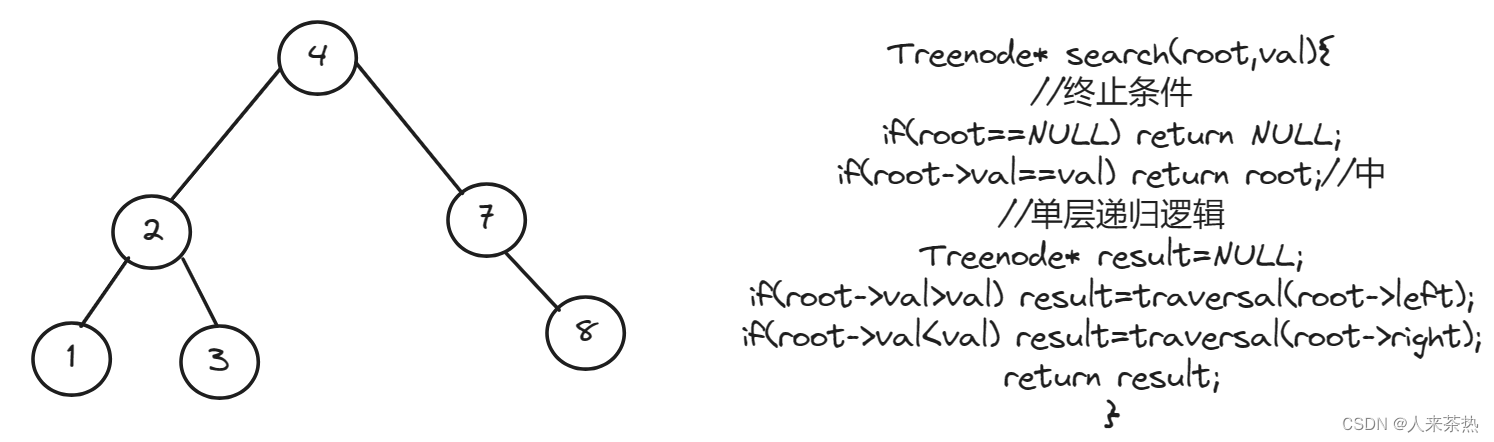
代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int val) {
        //终止条件
        if(root==NULL) return NULL;
        if(root->val==val) return root;
        //单层递归逻辑
        TreeNode* result;
        if(root->val>val) result = searchBST(root->left,val);
        if(root->val<val) result = searchBST(root->right,val);
        return result;
    }
};

迭代法（极其简单）

不用使用栈，不需要回溯过程，因为二叉搜索树的节点数值的性质帮我们确定了搜索顺序

伪代码

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int val) {
        while(root!=NULL){
            if(root->val>val) root = root->left;
            else if(root->val<val) root = root->right;
            else return root;
        }
        return NULL;
    }
};

题目4：98 验证二叉搜索树

题目链接：98 验证二叉搜索树

题意

判断一颗二叉树是否为有效的二叉搜索树，有效的二叉搜索树定义为：

1）节点的左子树的元素值均小于该节点

2）节点的右子树的元素值均大于该节点

3）左右节点的左右子树也为二叉搜索树

递归

递归三部曲：

1）确定递归函数的参数和返回值

2）确定终止条件

3）确定单层递归逻辑

数组

将二叉树中的每个元素按照中序遍历（左中右）的顺序，放入到数组中，然后判断数组是否是单调递增的即可

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> vec;
    void traversal(TreeNode* root){
        //终止条件
        if(root==NULL) return;
        //单层递归逻辑
        //中序遍历（左中右）
        traversal(root->left);
        vec.push_back(root->val);
        traversal(root->right);
    }
    bool isValidBST(TreeNode* root) {
         traversal(root);
         for(int i=0;i<vec.size();i++){
             if(i>=1 && vec[i]<=vec[i-1]) return false;
         }
         return true;
    }
};

直接判断数组是否有序（初始化最大值）

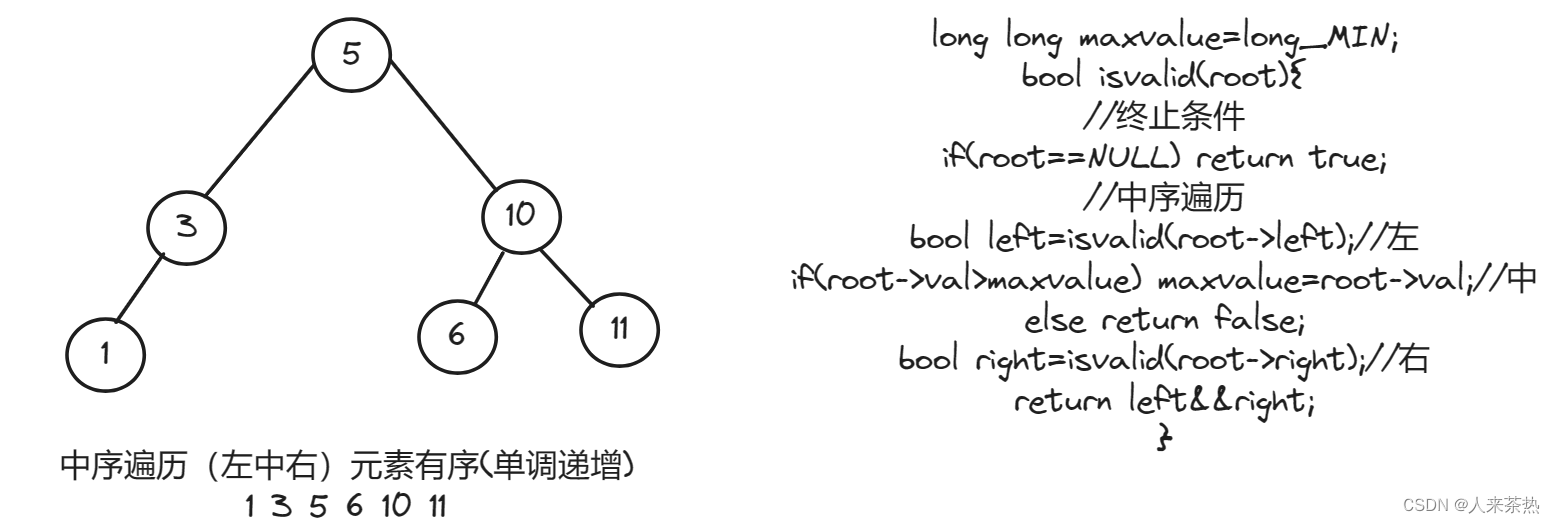
代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    long long maxvalue = LONG_MIN;
    bool isValidBST(TreeNode* root) {
         //终止条件
         if(root==NULL) return true;
         //单层递归逻辑
         //中序遍历，左中右
         bool left = isValidBST(root->left);//左
         if(maxvalue<root->val) maxvalue = root->val;//中
         else return false;
         bool right = isValidBST(root->right);//右
         return left && right;
    }
};

双指针优化（避免初始化最小值）

使用1个指针pre指向当前遍历节点的前一个节点，比较pre->val和root->val的大小

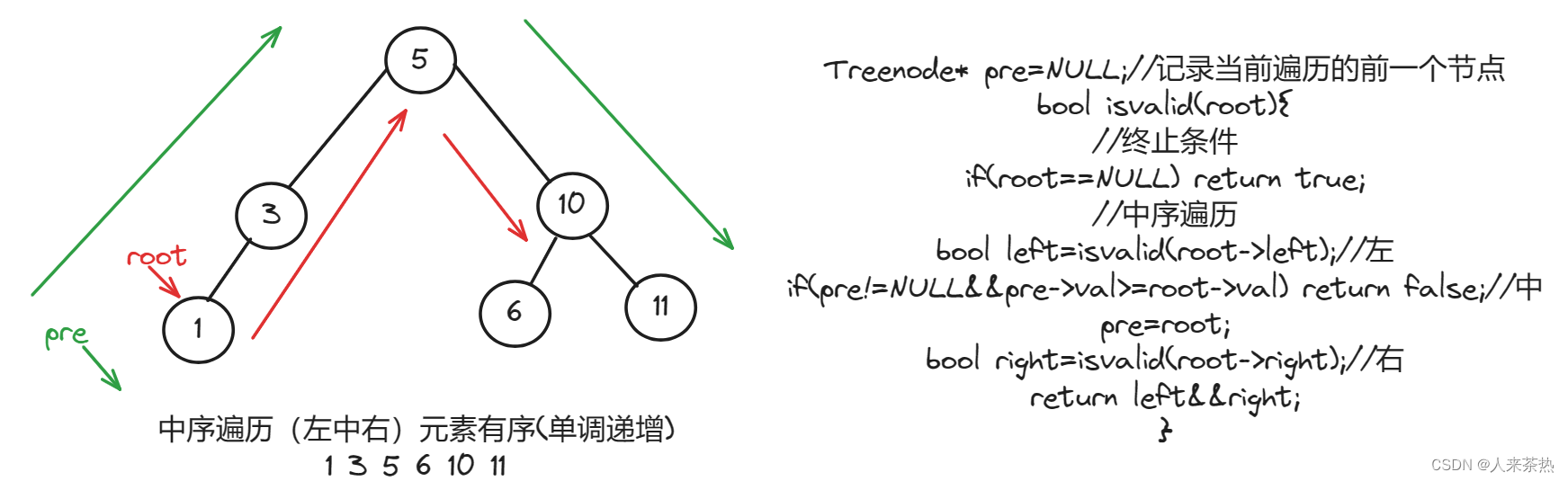
代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* pre = NULL;
    bool isValidBST(TreeNode* root) {
         //终止条件
         if(root==NULL) return true;
         //单层递归逻辑
         //中序遍历，左中右
         bool left = isValidBST(root->left);//左
         if(pre!=NULL && pre->val>=root->val) return false;//中
         pre = root;
         bool right = isValidBST(root->right);//右
         return left && right;
    }
};