LeetCode 1901. 寻找峰值 II

一、题目

1、题目描述

一个 2D 网格中的?峰值?是指那些?严格大于?其相邻格子(上、下、左、右)的元素。

给你一个?从 0 开始编号?的?m x n?矩阵?mat?，其中任意两个相邻格子的值都?不相同?。找出?任意一个 峰值?mat[i][j]?并?返回其位置?[i,j]?。

你可以假设整个矩阵周边环绕着一圈值为?-1?的格子。

要求必须写出时间复杂度为?O(m log(n))?或?O(n log(m))?的算法

2、接口描述

?

class Solution {
public:
    vector<int> findPeakGrid(vector<vector<int>>& mat) {
        
    }
};

3、原题链接

1901. 寻找峰值 II

---

二、解题报告

1、思路分析

我们先不考虑复杂度问题，我们贪心的想”人往高处走“，即我们选定初位置(0,0)往四个相邻位置上最大的方向走，最后一定会停留在一个比四个相邻位置都大，否则无法停留，这也就说明了峰值的存在性。

那么如果按照上述贪心方式走，我们最坏情况下是可以达到O(mn)的，如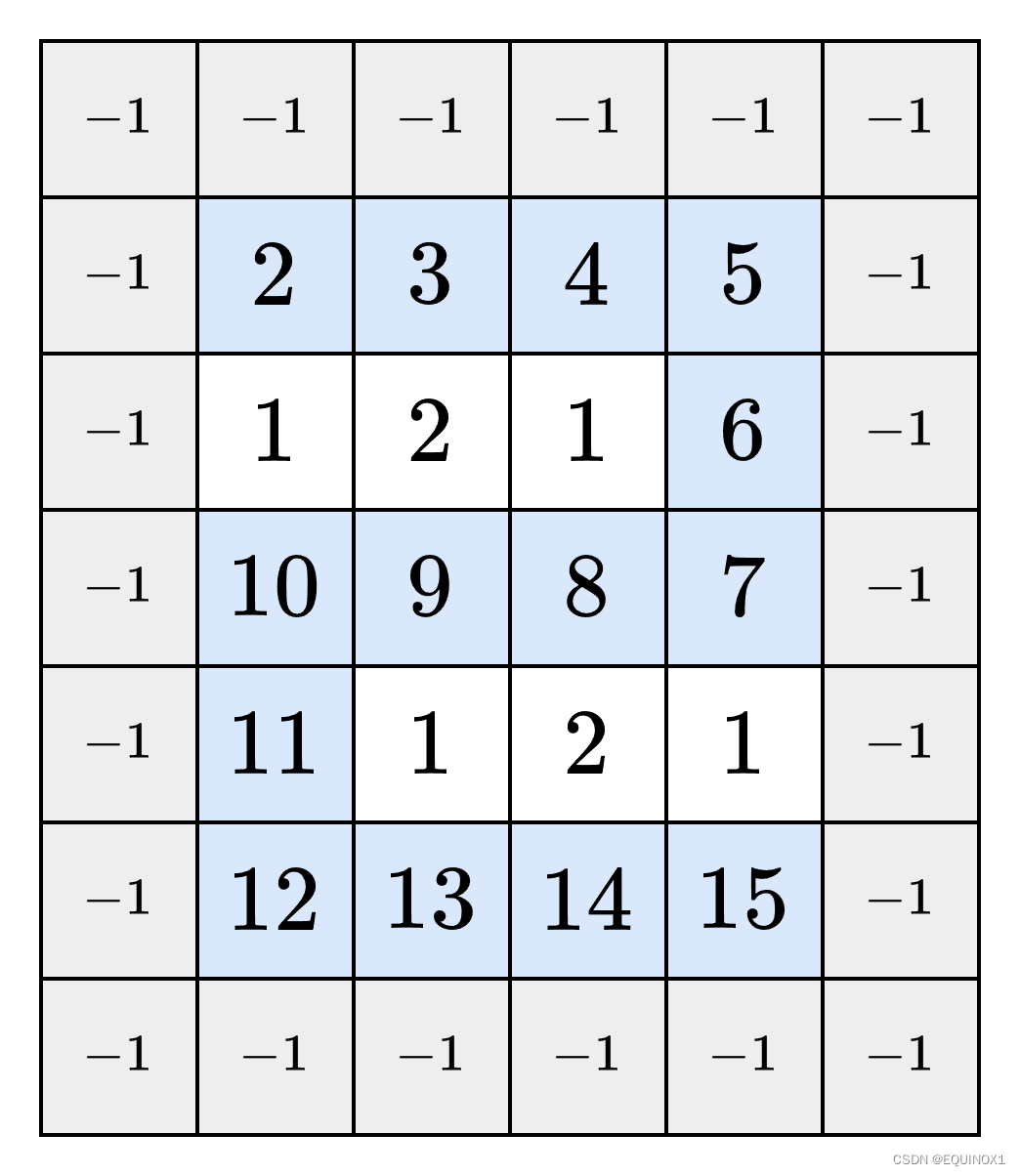

而且题目已经要求了O(nlogm)或者O(mlogn)的解法了，已经明示是二分了，我们不妨直接考虑二分的解法

能否按照昨天162. 寻找峰值的方式，每一行进行二分，返回符合比上下相邻的大的峰值呢？

当然不可以，因为每一行可以存在多个，我们162. 寻找峰值的方法只能找到一个，所以我们要另辟蹊径。

我们还是按照贪心思想“人往高处走”，对于第i行的最大值mat[i][j]，如果mat[i][j] < mat[i][j + 1]，那么我们往下面的行走，一定可以找到峰值

否则，我们往上走也一定可以找到峰值

这样每次行区间缩小一半，每次查找行最值需要一次遍历，正好符合题目要求的复杂度

2、复杂度

时间复杂度： O(nlogm) 空间复杂度：O(1)

3、代码详解

?

class Solution {
public:
    vector<int> findPeakGrid(vector<vector<int>>& mat) {
        int m = mat.size() , n = mat[0].size();
        function<int(int,int)> g = [&](int x , int y){
            if(x < 0 || y < 0 || x >= m || y >= n)
                return -1;
            return mat[x][y];
        };
        int l = 0 , r = m - 1;
        while(l < r)
        {
            int mid = (l + r) >> 1;
            int j = max_element(mat[mid].begin() , mat[mid].end()) - mat[mid].begin();
            if(g(mid , j) > g(mid + 1 , j))
                r = mid;
            else
                l = mid + 1;
        }
        r = max_element(mat[l].begin() , mat[l].end()) - mat[l].begin();
        return {l , r};
    }
};

g稚嫩g