【格密码】基于坏基的单向陷门函数

目录

一. 介绍

二. 好基与格陷门信息

三. 公钥密码方案

3.1 加密过程

3.2 解密过程

四. 签名方案

4.1 签名过程

4.2 验签过程

五. 与NTRU格的关系

六. 推荐阅读

---

一. 介绍

McEliece在1978年提出了基于编码的密码系统（code-based cryptosystem），随后在1997年GGH等人基于格的困难问题提出了一个加密方案和数字签名。相关文献：

[GGH97] O. Goldreich, S. Goldwasser, and S. Halevi. Public-key cryptosystems from lattice reduction problems. In CRYPTO, pages 112–131. 1997.

该方案的实用性很强，但很遗憾是基于启发式的，不具备最坏情况的安全性保证（worst case）。在2006年，对应的签名方案被攻破。

但是基于坏基的格密码方案为后续格陷门的设计提供了很好的思路。

二. 好基与格陷门信息

格密码里通常所说的坏基指的是那些很长且正交性很差的格基向量，当然对应的好基指的就是那些接近正交且长度较短的格基向量。

备注：一般情况下，格基越正交，格基向量长度越短。

对于同一个格来讲，我们就可以把好基作为私钥，把坏基作为公钥。也就是好基可以作为某些困难问题的陷门信息。

那么好基和坏基怎样同时产生呢？

步骤如下：

1. 随机产生好基
2. 生成幺模矩阵
3. 将好基乘以幺模矩阵即可以得到坏基

备注：任意格基乘以幺模矩阵，得到的格是保持不变的。

格密码中对应的最坏格基则是hermite标准矩阵。在实际设计公钥密码算法时，最好拿hermite标准矩阵作为公钥。

三. 公钥密码方案

3.1 加密过程

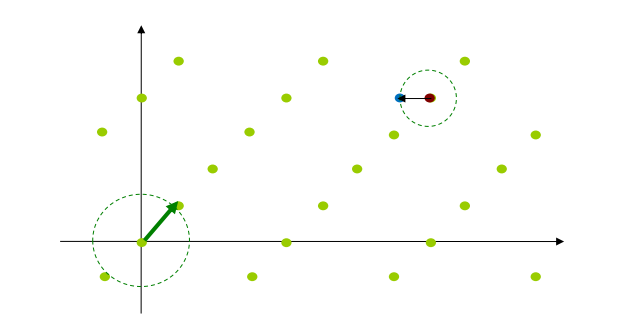
加密方根据明文信息，选择对应格点v，如下：

可以把此看成编码的过程。

接着选择一个比较小的误差项，也叫做噪声项，如下：

接着计算密文c，如下：

通常要求误差项e足够小，保证距离c最近的格点只有一个v，也就是解密之后对应一个明文。细心的话可以发现，从密文c恢复v的过程其实就是格上BDD问题（bounded distance decoding problem）。

3.2 解密过程

合法接收端拥有好基，则很容易从c求出v，然后恢复出明文信息。

对应的，窃听端只知道坏基，则不能从c推出v，在网络安全领域，我们希望窃听端不会获取关于明文v的任何信息，也就是实现所谓的语义安全。

四. 签名方案

4.1 签名过程

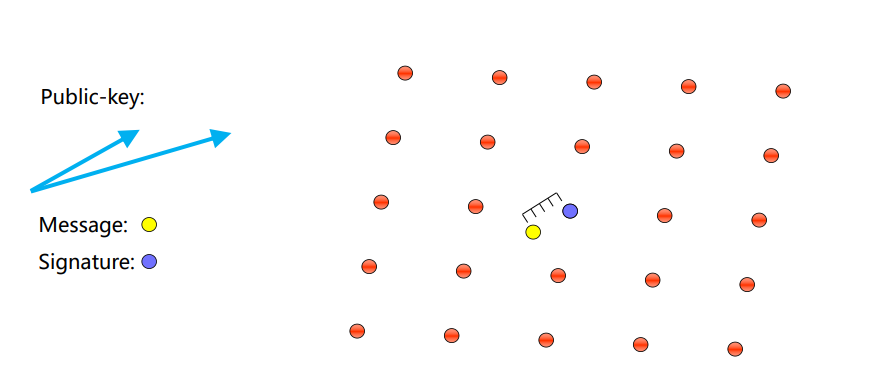
首先签名方将消息映射成一个实数点m：

当然这个过程可能会用到hash函数。

接着签名者根据好基找到离m最近的格点v：

该格点即为最终的签名。

4.2 验签过程

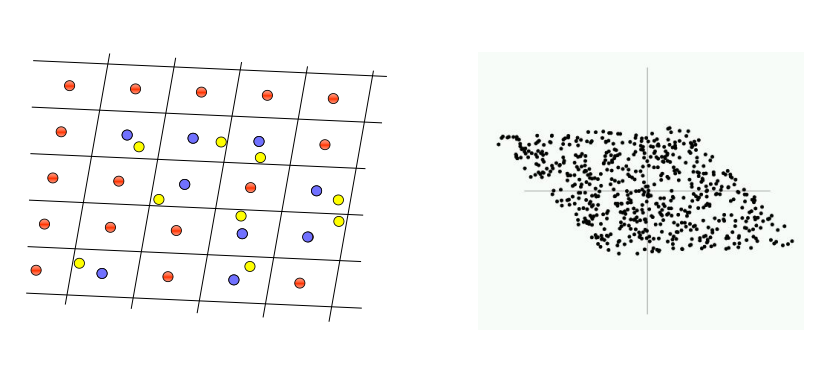
在已知明文安全下，伪造方只有坏基，对于一个未签名的消息m'，我们希望的是，它找不到离其最近的格点。

但历史发展告诉我们，2006年这个签名方案就被证明是不安全的。主要原因是签名的结果会邪路私钥好基的几何特征信息。在几轮签名以后，敌手就可以恢复出私基，然后就可以对任意消息进行伪造签名了。

五. 与NTRU格的关系

借鉴GGH97的思路，基于环结构的密码算法就出现了，也就是所谓的NTRU格。其实可以在签名过程当中再加入一些扰动，来保证签名结果泄露更少的私钥信息，当然这个过程不可避免的会增加参数的值和密钥的尺寸。这样操作就可以出现两个格，而且不想关，敌手攻击的难度会显著提升。当然，如果用现在最坏情况的安全性讨论的话，这些方案都不是那么安全。

六. 推荐阅读

（1）第一个实现了最坏情况的格密码安全方案

[Ajt96] M. Ajtai. Generating hard instances of lattice problems. Quaderni di Matematica, 13:1–32,
2004. Preliminary version in STOC 1996.

（2）基于编码的格密码方案

[McE78] R. J. McEliece. A public-key cryptosystem based on algebraic coding theory. DSN Progress Report 42-44, Jet Propulsion Laboratory, 1978.

（3）利用好基生成格陷门信息

[GGH97] O. Goldreich, S. Goldwasser, and S. Halevi. Public-key cryptosystems from lattice reduction problems. In CRYPTO, pages 112–131. 1997.

（4）攻击GGH97的签名方案

[NR06] P. Q. Nguyen and O. Regev. Learning a parallelepiped: Cryptanalysis of GGH and NTRU signatures. J. Cryptology, 22(2):139–160, 2009. Preliminary version in Eurocrypt 2006.

（5）解释Hermite标准式可以最为公钥格基

D. Micciancio. Improving lattice based cryptosystems using the Hermite normal form. In
CaLC, pages 126–145. 2001.

（6）解释NTRU格

?J. Hoffstein, J. Pipher, and J. H. Silverman. NSS: an NTRU lattice-based signature scheme. In
EUROCRYPT, pages 211–228. 2001.