leetcode - 2385. Amount of Time for Binary Tree to Be Infected
Description
You are given the root of a binary tree with unique values, and an integer start. At minute 0, an infection starts from the node with value start.
Each minute, a node becomes infected if:
The node is currently uninfected.
The node is adjacent to an infected node.
Return the number of minutes needed for the entire tree to be infected.
Example 1:
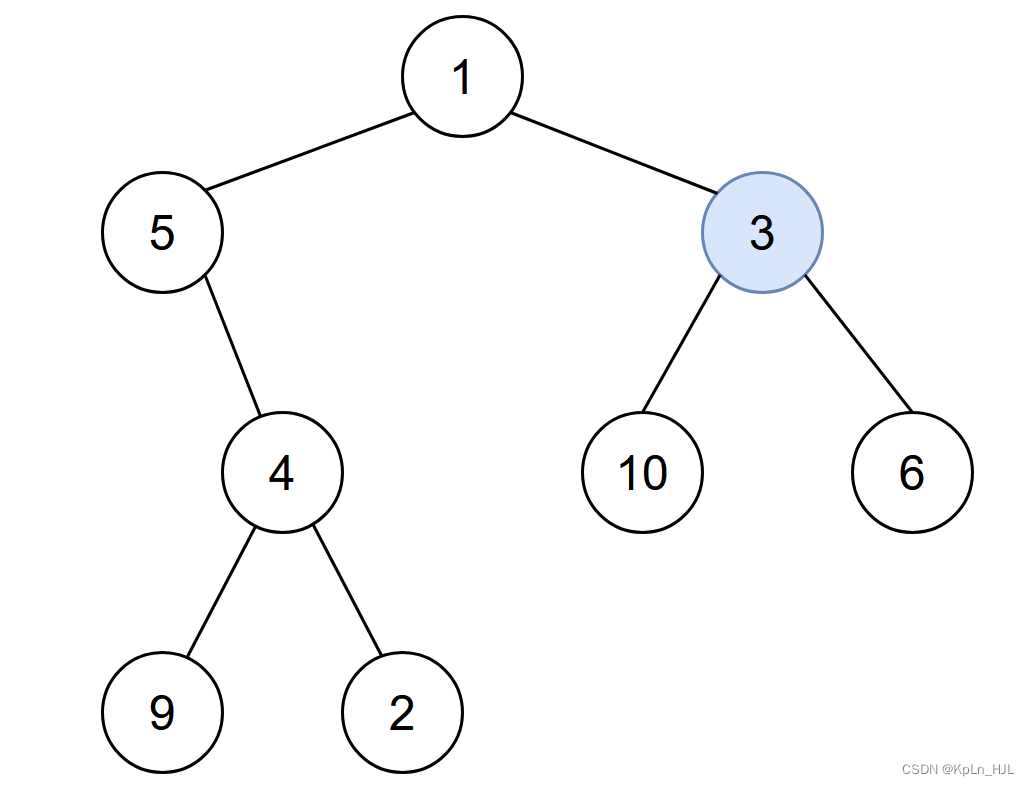
Input: root = [1,5,3,null,4,10,6,9,2], start = 3
Output: 4
Explanation: The following nodes are infected during:
-
Minute 0: Node 3
-
Minute 1: Nodes 1, 10 and 6
-
Minute 2: Node 5
-
Minute 3: Node 4
-
Minute 4: Nodes 9 and 2
It takes 4 minutes for the whole tree to be infected so we return 4.
Example 2:

Input: root = [1], start = 1
Output: 0
Explanation: At minute 0, the only node in the tree is infected so we return 0.
Constraints:
The number of nodes in the tree is in the range [1, 10^5].
1 <= Node.val <= 10^5
Each node has a unique value.
A node with a value of start exists in the tree.
Solution
Solved after hints, at first I thought I could use math and level traversal to solve this, but it turned out to be easier if transform the tree into a graph.
Hint: Transform the tree into a non-directional graph, then the answer is the longest road in the graph.
Time complexity:
o
(
n
)
o(n)
o(n)
Space complexity:
o
(
n
)
o(n)
o(n)
Code
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def amountOfTime(self, root: Optional[TreeNode], start: int) -> int:
graph = {}
# dfs to build graph
stack = [root]
while stack:
node = stack.pop()
if node.val not in graph:
graph[node.val] = []
if node.right:
graph[node.val].append(node.right.val)
if node.right.val not in graph:
graph[node.right.val] = []
graph[node.right.val].append(node.val)
stack.append(node.right)
if node.left:
graph[node.val].append(node.left.val)
if node.left.val not in graph:
graph[node.left.val] = []
graph[node.left.val].append(node.val)
stack.append(node.left)
# bfs to get the farest node
queue = collections.deque([(start, 0)])
res = 0
visited = set()
while queue:
node, step = queue.popleft()
if node in visited:
continue
visited.add(node)
res = max(res, step)
for neighbor in graph[node]:
queue.append((neighbor, step + 1))
return res
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 2.3_5 信号量机制
- PLC水箱液位控制、神经网络、PID模糊控制等Factory IO仿真
- Linux软连接
- 如何一眼分辨哪个U盘的接口更快?
- MES系统中的工时管理,提高制造业工厂的生产效率
- vue3 + TypeScript使用国际化
- thinkadmin安装步骤
- 【考研数学】08早鸟课 (函数)连续与间断
- C++精进之路(十一)使用类
- 利用MultCloud在线复制传输不同网盘之间的数据:支持谷歌Drive、百度网盘等