基于神经网络的电力系统的负荷预测

一、背景介绍：

电力系统负荷预测是生产部门的重要工作之一，通过准确的负荷预测，可以经济合理地安排机组的启停、减少旋转备用容量、合理安排检修计划、降低发电成本和提高经济效益。负荷预测按预测的时间可以分为长期、中期和短期负荷预测。其中，短期负荷预测中，周负 荷预测(未来1周)、日负荷预测(未来24小时)及提前小时预测对于电力系统的实时运行 调度至关重要。负荷预测对电力系统控制、运行和计划都有着重要意义。因为对未来时刻进 行预调度要以负荷预测的结果为依据，负荷预测结果的准确性将直接影响调度的结果，从而 对电力系统的安全稳定运行和经济性带来重要影响。

电力系统负荷变化受多方面的影响。一方面，存在着由于未知不确定因素引起 的随机波动；另一方面，又具有周期变化的规律性，这也使得负荷曲线具有相似性。同时，由于受天气、节假日等特殊情况影响，致使负荷变化出现差异。假设某电力系统在过去12天的有功负荷值，以及有关气象特征经归一化后的数据如表1所示。

表1 ??电力系统负荷变化样本集

日期	电 力 负 荷												气?象?特?征
1	0.2452	0.1466	0.1314	0.2243	0.5523	0.6642	0.7015	0.6981	0.6821	0.6945	0.7549	0.8215
2	0.2217	0.1581	0.1408	0.2304	0.5134	0.5312	0.6819	0.7125	0.7265	0.6847	0.7826	0.8325	0.2415	0.3027	0
3	0.2525	0.1627	0.1507	0.2406	0.5502	0.5636	0.7051	0.7352	0.7459	0.7015	0.8064	0.8156	0.2385	0.3125	0
4	0.2016	0.1105	0.1243	0.1978	0.5021	0.5232	0.6819	0.6952	0.7015	0.6825	0.7825	0.7895	0.2216	0.2701	0
5	0.2115	0.1201	0.1312	0.2019	0.5532	0.5736	0.7029	0.7032	0.7189	0.7019	0.7965	0.8025	0.2352	0.2506	0.5
6	0.2335	0.1322	0.1534	0.2214	0.5623	0.5827	0.7198	0.7276	0.7359	0.7506	0.8092	0.8221	0.2542	0.3125	0
7	0.2368	0.1432	0.1653	0.2205	0.5823	0.5971	0.7136	0.7129	0.7263	0.7153	0.8091	0.8217	0.2601	0.3198	0
8	0.2342	0.1368	0.1602	0.2131	0.5726	0.5822	0.7101	0.7098	0.7127	0.7121	0.7995	0.8126	0.2579	0.3099	0
9	0.2113	0.1212	0.1305	0.1819	0.4952	0.5312	0.6886	0.6898	0.6999	0.7323	0.7721	0.7956	0.2301	0.2867	0.5
10	0.2005	0.1121	0.1207	0.1605	0.4556	0.5022	0.6553	0.6673	0.6798	0.7023	0.7521	0.7756	0.2234	0.2799	1
11	0.2123	0.1257	0.1343	0.2079	0.5579	0.5716	0.7059	0.7145	0.7205	0.7401	0.8019	0.8136	0.2314	0.2977	0
12	0.2119	0.1215	0.1621	0.2161	0.6171	0.6159]	0.7155	0.7201	0.7243	0.7298	0.8179	0.8229	0.2317	0.2936	0

在表1中，由于电力负荷每隔2个小时测量1次，故一天共有12组负荷数据。而气象特征分别为预测日的最高气温、最低气温和天气特征值，其中分别用0表示晴、0.5表示阴天和1表示雨天等天气特征。

试根据电力系统以前的电力负荷和当日的气象特征预测当日的电力负荷。

求解提示：

①确定训练样本集

② 网络设计和训练伪代码

net=newff(minmax(X),[* *],{?});

net.trainParam.epochs=100;

net.trainParam.goal=0.001;

net=train(net,X,T);

y=sim(net,X);

③?网络测试

网络训练成功后，利用测试样本对网络进行测试。测试样本由表1中的第11 天 的 1 2组实际负荷数据和第12天的预测日当天的3个气象特征值组成，

Xtest

ytest=sim(net,Xtest)

• 工程实现：

用BP网络预测电力负荷

1)网络创建

BP一般分为3层输入层,中间层（隐藏层),输出层。

通过单隐层的BP网络实现。由于输入量有15个元素，所以网络输出层的神经元有15个,根据Kolmogorov定理网络中间层神经元取31神经元为最佳。根据12个输出向量定义输出层的神经元为12个。网络中间层神经元传递函数采用S型正切函网络经过训练后才可以用于电力负荷预测的实际应用。考虑到网络的结构比较复杂，神经网络元个数比较多，需要适当增大训练次数和学习速率。训练参数的设定如表4。3所示

训练参数表

训练次数	训练目标	学习速率
10000	0.001	0.01

有关程序如下：

net.trainParam。epochs=10000；

net.trainParam。goal=0.001；

LP.lr=0.01；

3)网络测试

输出层神经元函数采用S型对数函数logsig。因为输出数据位于［0，1]之间。输入量的［0,1］之间用变量threshold来规定。Bp的网络训练函数为trainlm,所以在newff中调用trainlm函数。

把输出值减去实际值之后再除以实际值就是数据的相对误差了，matlab的程序如下所示：

????z=y—X;

????c=X.\z;

????plot（1:12，c);

????grid；

????title('相对误差曲线’)；

????xlabel(’时间’)；

????ylabel（’相对误差率’）；

训练过程可视化如下

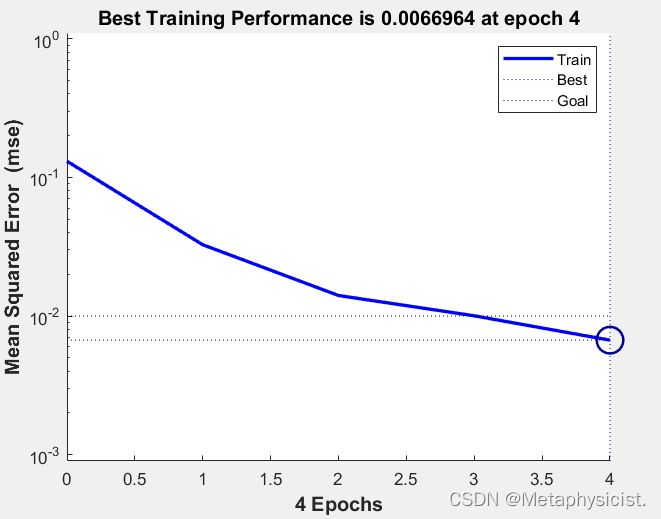
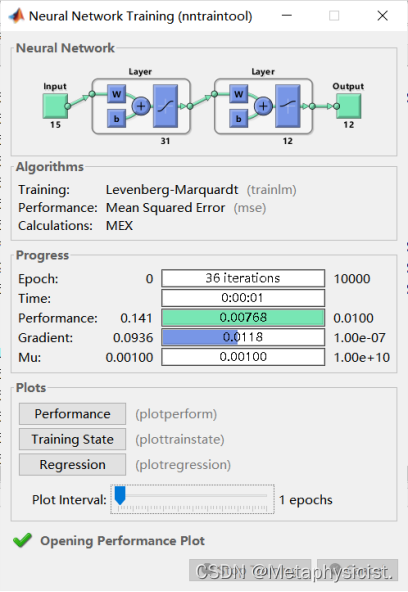
BP神经网络MATLAB语法

1. 数据预处理

在训练神经网络前一般需要对数据进行预处理，一种重要的预处理手段是归一化处理。下面简要介绍归一化处理的原理与方法。

(1) 什么是归一化？

数据归一化，就是将数据映射到[0,1]或[-1,1]区间或更小的区间，比如(0.1,0.9) 。

(2) 为什么要归一化？

<1>输入数据的单位不一样，有些数据的范围可能特别大，导致的结果是神经网络收敛慢、训练时间长。

<2>数据范围大的输入在模式分类中的作用可能会偏大，而数据范围小的输入作用就可能会偏小。

<3>由于神经网络输出层的激活函数的值域是有限制的，因此需要将网络训练的目标数据映射到激活函数的值域。例如神经网络的输出层若采用S形激活函数，由于S形函数的值域限制在(0,1)，也就是说神经网络的输出只能限制在(0,1)，所以训练数据的输出就要归一化到[0,1]区间。

<4>S形激活函数在(0,1)区间以外区域很平缓，区分度太小。例如S形函数f(X)在参数a=1时，f(100)与f(5)只相差0.0067。

(3) 归一化算法

　　一种简单而快速的归一化算法是线性转换算法。线性转换算法常见有两种形式：

<1> y = ( x - min )/( max - min )

　　其中min为x的最小值，max为x的最大值，输入向量为x，归一化后的输出向量为y 。上式将数据归一化到 [ 0 , 1 ]区间，当激活函数采用S形函数时（值域为(0,1)）时这条式子适用。

<2> y = 2 * ( x - min ) / ( max - min ) - 1

这条公式将数据归一化到 [ -1 , 1 ] 区间。当激活函数采用双极S形函数（值域为(-1,1)）时这条式子适用。

(4) Matlab数据归一化处理函数

Matlab中归一化处理数据可以采用premnmx ， postmnmx ， tramnmx 这3个函数。

<1> premnmx

语法：[pn,minp,maxp,tn,mint,maxt] = premnmx(p,t)

参数：

pn： p矩阵按行归一化后的矩阵

minp，maxp：p矩阵每一行的最小值，最大值

tn：t矩阵按行归一化后的矩阵

mint，maxt：t矩阵每一行的最小值，最大值

作用：将矩阵p，t归一化到[-1,1] ，主要用于归一化处理训练数据集。

<2> tramnmx

语法：[pn] = tramnmx(p,minp,maxp)

参数：

minp，maxp：premnmx函数计算的矩阵的最小，最大值

pn：归一化后的矩阵

作用：主要用于归一化处理待分类的输入数据。

<3> postmnmx

语法： [p,t] = postmnmx(pn,minp,maxp,tn,mint,maxt)

参数：

minp，maxp：premnmx函数计算的p矩阵每行的最小值，最大值

mint，maxt：premnmx函数计算的t矩阵每行的最小值，最大值

作用：将矩阵pn，tn映射回归一化处理前的范围。postmnmx函数主要用于将神经网络的输出结果映射回归一化前的数据范围。

2. 使用Matlab实现神经网络

使用Matlab建立前馈神经网络主要会使用到下面3个函数：

newff ：前馈网络创建函数

train：训练一个神经网络

sim ：使用网络进行仿真

下面简要介绍这3个函数的用法。

(1) newff函数

<1>语法

newff函数参数列表有很多的可选参数，具体可以参考帮助文档，这里介绍一种简单形式。

语法：net = newff ( A, B, {C} ,‘trainFun’)

参数：

A：一个n×2的矩阵，第i行元素为输入信号xi的最小值和最大值；

B：一个k维行向量，其元素为网络中各层节点数；

C：一个k维字符串行向量，每一分量为对应层神经元的激活函数；

trainFun ：为学习规则采用的训练算法。

表3.1 BP网络的常用函数表

函数类型	函数名称	函数用途
前向网络创建函数	newcf	创建级联前向网络
	Newff	创建前向BP网络
传递函数	logsig	S型的对数函数
	tansig	S型的正切函数
	purelin	纯线性函数
学习函数	learngd	基于梯度下降法的学习函数
	learngdm	梯度下降动量学习函数
性能函数	mse	均方误差函数
	msereg	均方误差规范化函数
显示函数	plotperf	绘制网络的性能
	plotes	绘制一个单独神经元的误差曲面
	plotep	绘制权值和阈值在误差曲面上的位置
	errsurf	计算单个神经元的误差曲面

newff函数用于创建一个BP网络。调用格式为：

net=newff

net=newff(PR,[S1 S2..SN1],{TF1 TF2..TFN1},BTF,BLF,PF)

其中，net=newff;用于在对话框中创建一个BP网络。

net为创建的新BP神经网络；

PR为网络输入向量取值范围的矩阵；

[S1 S2…SNl]表示网络隐含层和输出层神经元的个数；

{TFl TF2…TFN1}表示网络隐含层和输出层的传输函数，默认为‘tansig’；

BTF表示网络的训练函数，默认为‘trainlm’；

BLF表示网络的权值学习函数，默认为‘learngdm’；

PF表示性能数，默认为‘mse’。

<2>常用的激活函数

　　常用的激活函数有：

a) 线性函数?(Linear transfer function)

　　该函数的字符串为’purelin’。

b) 对数S形转移函数( Logarithmic sigmoid transfer function )

该函数的字符串为’logsig’。

c) 双曲正切S形函数?(Hyperbolic tangent sigmoid transfer function )

该函数的字符串为’tansig’。

Matlab的安装目录下的toolbox\nnet\nnet\nntransfer子目录中有所有激活函数的定义说明。

<3>常见的训练函数

常见的训练函数有：

traingd ：梯度下降BP训练函数(Gradient descent backpropagation)

traingdx ：梯度下降自适应学习率训练函数

<4>网络配置参数

一些重要的网络配置参数如下：

net.trainparam.goal ：神经网络训练的目标误差

net.trainparam.show： 显示中间结果的周期

net.trainparam.epochs ：最大迭代次数

net.trainParam.lr： 学习率

(2) train函数

网络训练学习函数。

语法：[ net, tr, Y1, E ] = train( net, X, Y )

参数：

X：网络实际输入

Y：网络应有输出

tr：训练跟踪信息

Y1：网络实际输出

E：误差矩阵

(3) sim函数

语法：Y=sim(net,X)

参数：

net：网络

X：输入给网络的Ｋ×N矩阵，其中K为网络输入个数，N为数据样本数

Y：输出矩阵Q×N，其中Q为网络输出个数

• 源代码：

% 定义输入数据矩阵P

P=[0.2452 0.1466 0.1314 0.2243 0.5523 0.6642 0.7105 0.6981 0.6821 0.6945 0.7549 0.8215 0.2415 0.3027 0;

????0.2217 0.1581 0.1408 0.2304 0.5134 0.5312 0.6819 0.7125 0.7265 0.6847 0.7826 0.8325 0.2385 0.3125 0;

????0.2525 0.1627 0.1507 0.2406 0.5502 0.5636 0.7051 0.7352 0.7459 0.7015 0.8064 0.8156 0.2216 ?0.2701 1;

????0.2016 0.1105 0.1243 0.1978 0.5021 0.5232 0.6819 0.6952 0.7015 0.6825 0.7825 0.7895 0.2352 0.2506 0.5;

????0.2115 0.1201 0.1312 0.2019 0.5332 0.5736 0.7029 0.7032 0.7189 0.7019 0.7965 0.8025 0.2542 0.3125 0;

????0.2335 0.1322 0.1534 0.2214 0.5623 0.5827 0.7198 0.7276 0.7359 0.7506 0.8092 0.8221 0.2601 0.3198 0;

????0.2368 0.1432 0.1653 0.2205 0.5823 0.5971 0.7136 0.7129 0.7263 0.7153 0.8091 0.8217 0.2579 0.3099 0;

???0.2342 0.1368 0.1602 0.2131 0.5726 0.5822 0.7101 0.7098 0.7127 0.7121 0.7995 0.7126 0.2301 0.2867 0.5;

???0.2113 0.1212 0.1305 0.1819 0.4952 0.5312 0.6886 0.6898 0.6999 0.7323 0.7721 0.7956 0.2234 0.2799 1;

???0.2005 0.1121 0.1207 0.1605 0.4556 0.5022 0.6553 0.6673 0.6798 0.7023 0.7521 0.7756 0.2314 0.2977 0]';

?

% 定义目标数据矩阵T

T=[0.2217 0.1581 0.1408 0.2304 0.5134 0.5312 0.6819 0.7125 0.7265 0.6847 0.7826 0.8325;

????0.2525 0.1627 0.1507 0.2406 0.5502 0.5636 0.7051 0.7352 0.7459 0.7015 0.8064 0.8156;

????0.2016 0.1105 0.1243 0.1978 0.5021 0.5232 0.6819 0.6952 0.7015 0.6825 0.7825 0.7895;

????0.2115 0.1201 0.1312 0.2019 0.5532 0.5736 0.7029 0.7032 0.7189 0.7019 0.7965 0.8025;

????0.2335 0.1322 0.1534 0.2214 0.5623 0.5827 0.7198 0.7276 0.7359 0.7506 0.8092 ?0.8221;

????0.2368 0.1432 0.1653 0.2205 0.5823 0.5971 0.7136 0.7129 0.7263 0.7153 0.8091 0.8217;

????0.2342 0.7368 0.1602 0.2131 0.5726 0.5822 0.7101 0.7098 0.7127 0.7121 0.7995 0.8126;

????0.2113 0.1212 0.1305 0.1819 0.4952 0.5312 0.6886 0.6898 0.6999 0.7323 0.7721 0.7956;

????0.2005 0.1121 0.1207 0.1605 0.4556 0.5022 0.6552 0.6673 0.6798 0.7023 0.7521 0.7756;

????0.2123 0.1257 0.1343 0.2079 0.5579 0.5716 0.7059 0.7145 0.7205 0.7401 0.8019 0.8136]';

threshold=[0 1;0 1;0 1;0 1;0 1;0 1;0 1;0 1;0 1;0 1;0 1;0 1;0 1;0 1;0 1;];

?

% 构建网络结构

net=newff(threshold,[31,12],{'tansig','logsig'},'trainlm');

?

% 设置训练参数

net.trainParam.epochs=10000;

net.trainParam.goal=0.001;

LP.lr=0.01;

net=train(net,P,T);

?

% 定义测试数据

P_test=[0.2123 0.1257 0.1343 0.2079 0.5579 0.5716 0.7059 0.7145 0.7205 0.7401 0.8019 0.8136 0.2317 0.3936 0]';

?

% 测试并得到预测结果

y=sim(net,P_test);

?

% 定义真实结果

X=[0.2119 0.1215 0.1621 0.2161 0.6171 0.6159 0.7155 0.7201 0.7243 0.7298 0.8179 0.8229]';

?

% 计算预测误差

?z=y-X;

?c=X.\z;

?

?% 绘制预测相对误差曲线

plot(1:12,c);

grid;

title('相对误差曲线');

xlabel('时间');

ylabel('相对误差率');