非递归实现归并排序

目录

非递归的归并排序

非递归的归并排序

实现流程参考图：

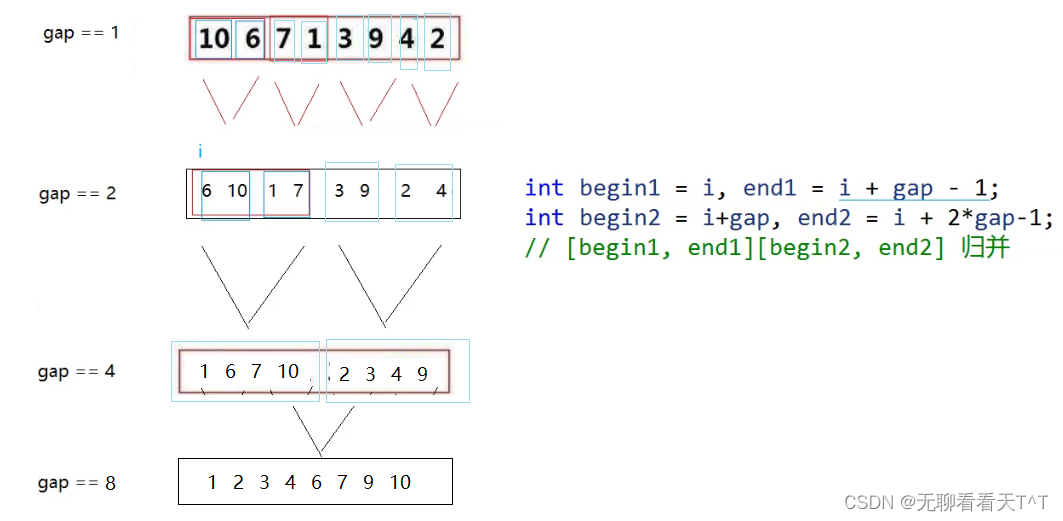
1、像递归实现归并排序一样，开辟n个空间大小的临时数组

2、利用变量gap模仿递归的过程，gap表示归并时的每组数据的个数

3、利用while循环实现归并，并且每一次我们要的都是两两一组的归并排序，所以在每次归并排序完之后（每次while循环结束）还要将gap*2为下一次更大范围的归并做准备，同时归并时每组的数据个数不能大于原数组本身的数据个数之和n（不能越界）

4、利用for循环实现归并的具体操作，i表示每次要归并的数组首元素的下标，初始值为0，以单趟排序的思路来看，当我们将10和6归并排序完成后，应该进行的是7和1之间的归并排序，此时i的值应该发生变化（开始第二次for循环）i = i + gap * 2，i应该在原来的基础上加上每次归并的数组元素个数*2（具体原因请自行理解）?

5、非递归实现的归并排序中的大多数代码都可以借鉴递归实现的归并排序，直接写出这样的代码可能有些困难，所以建议在看代码时以单趟排序自行理解，下面是一个不完整的非递归归并排序

//非递归递归排序
void MergeSortNonR(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		perror("malloc fail");
		return;
	}

	int gap = 1;//gap用于表示归并时的每组数据的个数
	while (gap < n)
	{
		printf("gap:%2d->", gap);
		for (size_t i = 0; i < n; i += 2 * gap)
		{
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i + gap, end2 = i + 2 * gap - 1;
			int j = begin1;
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] < a[begin2])
				{
					tmp[j++] = a[begin1++];
				}
				else
				{
					tmp[j++] = a[begin2++];
				}
			}

			while (begin1 <= end1)
			{
				tmp[j++] = a[begin1++];
			}

			while (begin2 <= end2)
			{
				tmp[j++] = a[begin2++];
			}

			memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));
		}

		printf("\n");

		gap *= 2;
	}


	free(tmp);
}

6、由于我们处理的原数组并不一定每次都可以像8个数据那样完美的归并，就比如下面的9和10一样，我们也想让它们进行归并，但是如果还是之前的代码，在归并过程中的end2与begin2的值就会发生越界，那么在后序while循环中就会出错

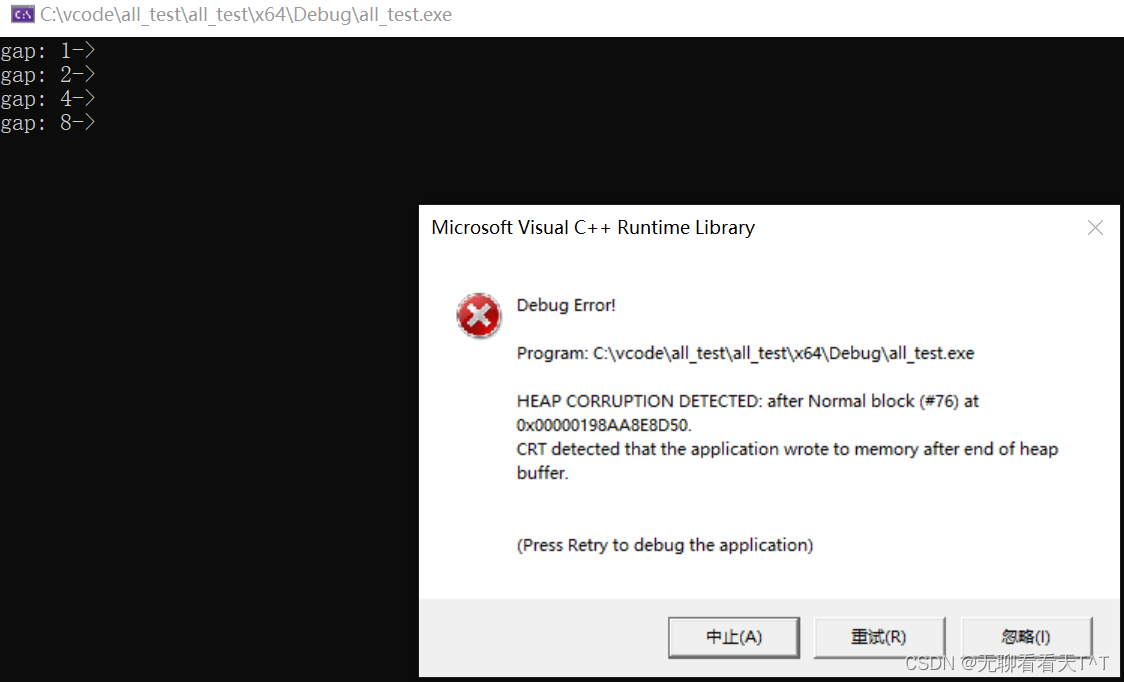
7、所以为了应对[10,11]或者[8,15]之类的越界情况，我们还需要进行边界处理的操作，即当end1大于等于n（end1等于n，后面begin2肯定越界）或者begin2大于等于n时（begin2等于n，后面的end2肯定越界）应该结束此次循环，证明此时后面的已经没有有效数据需要进行归并了

8、当end2大于等于n时，我们可以对end2进行修正，让它的大小重新回到正常即n-1（end2每次的值都应该是原数组末尾元素的下标）

9、最后还需要注意的是对于归并后的memcpy，需要在每次归并完成后（for循环）进行拷贝，而不是放在最后进行拷贝（while循环结束后）

//非递归递归排序
void MergeSortNonR(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		perror("malloc fail");
		return;
	}

	int gap = 1;//gap用于表示归并时的每组数据的个数
	while (gap < n)
	{
		printf("gap:%2d->", gap);
		for (size_t i = 0; i < n; i += 2 * gap)
		{
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i + gap, end2 = i + 2 * gap - 1;
			// [begin1, end1][begin2, end2] 归并
			//printf("[%2d,%2d][%2d, %2d] ", begin1, end1, begin2, end2);

			// 边界的处理
			if (end1 >= n || begin2 >= n)
			{
				break;
			}

			if (end2 >= n)
			{
				end2 = n - 1;
			}

			/*printf("[%2d,%2d][%2d, %2d] ", begin1, end1, begin2, end2);*/

			int j = begin1;
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] < a[begin2])
				{
					tmp[j++] = a[begin1++];
				}
				else
				{
					tmp[j++] = a[begin2++];
				}
			}

			while (begin1 <= end1)
			{
				tmp[j++] = a[begin1++];
			}

			while (begin2 <= end2)
			{
				tmp[j++] = a[begin2++];
			}

			memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));
		}

		printf("\n");

		gap *= 2;
	}


	free(tmp);
}

~over~