力扣每日一题99：恢复二叉搜索树

题目

给你二叉搜索树的根节点?root?，该树中的?恰好?两个节点的值被错误地交换。请在不改变其结构的情况下，恢复这棵树?。

示例 1：

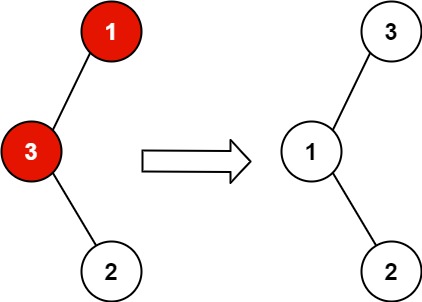
输入：root = [1,3,null,null,2]
输出：[3,1,null,null,2]
解释：3 不能是 1 的左孩子，因为 3 > 1 。交换 1 和 3 使二叉搜索树有效。

示例 2：

输入：root = [3,1,4,null,null,2]
输出：[2,1,4,null,null,3]
解释：2 不能在 3 的右子树中，因为 2 < 3 。交换 2 和 3 使二叉搜索树有效。

提示：

• 树上节点的数目在范围?[2, 1000]?内
• -231 <= Node.val <= 231 - 1

进阶：使用?O(n)?空间复杂度的解法很容易实现。你能想出一个只使用?O(1)?空间的解决方案吗？

通过次数

146.4K

提交次数

242.3K

通过率

60.5%

分析

二叉搜索树中序遍历是有序的（a[i]<a[i+1]），错误交换两个节点后，存在两个地方（a[i]>a[i+1]），如果两个地方重复了，那就是一个地方。

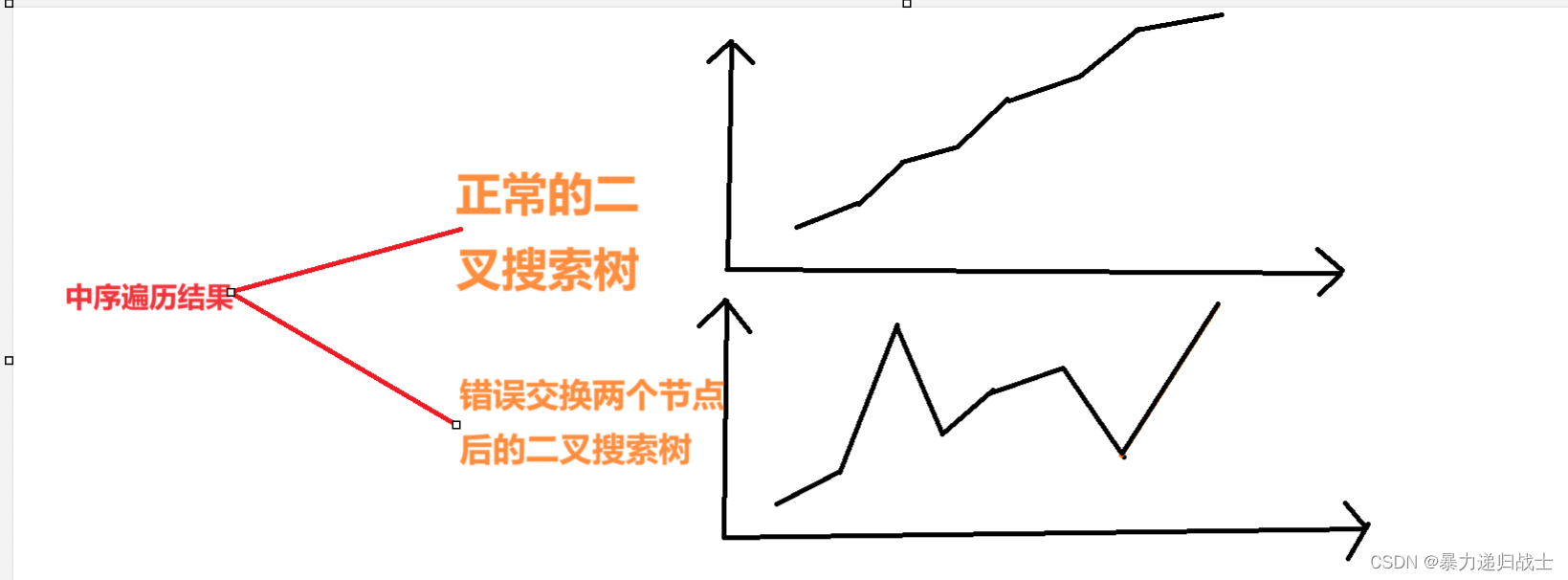
所以我们只要根据a[i]>a[i+1]这一特性找的错误交换的两个点换回来就行了。

普通方法：设置数组存放数据。时间O(N)，空间O(N)

中序遍历依次二叉树，同时将每个节点的地址和值分别放在一个数组里。然后再遍历记录数值的数组，找到要交换的两个位置。

class Solution {
public:
    void dfs(int arr[],TreeNode* adress[],int &pos,TreeNode* root)
    {
        if(!root) return;
        dfs(arr,adress,pos,root->left);
        arr[pos]=root->val;
        adress[pos]=root;
        pos++;
        dfs(arr,adress,pos,root->right);
    }
    void recoverTree(TreeNode* root) {
        TreeNode *adress[1000];
        int arr[1000];
        int pos=0;
        dfs(arr,adress,pos,root);
        int t1=-1,t2=0;
        for(int i=0;i<pos-1;i++)
        {
            //cout<<arr[i]<<",";
            if(arr[i]>arr[i+1])
            {
                if(t1==-1)
                {t1=i;t2=i+1;}
                else t2=i+1;
            }
        }
        //cout<<arr[pos-1];
        //cout<<"\nt1="<<t1<<"   t2="<<t2;
        int t=adress[t1]->val;
        adress[t1]->val=adress[t2]->val;
        adress[t2]->val=t;
    }
};

进阶：中序遍历，栈记录前驱。时间O(N),空间(H)，H为树的高度。

前面的方法是找到要交换连个节点的地址，然后交换值。我们用了一个数组记录所有节点的地址。其实我们就交换两个数，记录两个地址就行了。用二叉树的迭代法遍历可以用栈存放遍历的前驱，刚好符合了i和i+1的关系。下面是官方题解。

class Solution {
public:
    void recoverTree(TreeNode* root) {
        stack<TreeNode*> stk;
        TreeNode* x = nullptr;
        TreeNode* y = nullptr;
        TreeNode* pred = nullptr;

        while (!stk.empty() || root != nullptr) {
            while (root != nullptr) {
                stk.push(root);
                root = root->left;
            }
            root = stk.top();
            stk.pop();
            if (pred != nullptr && root->val < pred->val) {
                y = root;
                if (x == nullptr) {
                    x = pred;
                }
                else break;
            }
            pred = root;
            root = root->right;
        }

        swap(x->val, y->val);
    }
};

高阶：Morris遍历，时间O(N)，空间O(1)

废话不多说，看官方题解的代码。

class Solution {
public:
    void recoverTree(TreeNode* root) {
        TreeNode *x = nullptr, *y = nullptr, *pred = nullptr, *predecessor = nullptr;

        while (root != nullptr) {
            if (root->left != nullptr) {
                // predecessor 节点就是当前 root 节点向左走一步，然后一直向右走至无法走为止
                predecessor = root->left;
                while (predecessor->right != nullptr && predecessor->right != root) {
                    predecessor = predecessor->right;
                }
                
                // 让 predecessor 的右指针指向 root，继续遍历左子树
                if (predecessor->right == nullptr) {
                    predecessor->right = root;
                    root = root->left;
                }
                // 说明左子树已经访问完了，我们需要断开链接
                else {
                    if (pred != nullptr && root->val < pred->val) {
                        y = root;
                        if (x == nullptr) {
                            x = pred;
                        }
                    }
                    pred = root;

                    predecessor->right = nullptr;
                    root = root->right;
                }
            }
            // 如果没有左孩子，则直接访问右孩子
            else {
                if (pred != nullptr && root->val < pred->val) {
                    y = root;
                    if (x == nullptr) {
                        x = pred;
                    }
                }
                pred = root;
                root = root->right;
            }
        }
        swap(x->val, y->val);
    }
};