代码随想录算法训练营第三十四天（贪心算法篇）|10.2 分发饼干，376. 摆动序列，53. 最大子序和

理论基础

贪心的本质是选择每一阶段的局部最优，从而实现全局最优。

e.g. 一堆钞票，能拿走十张，想要拿走最大数额的钱。

? ? ? ?局部最优：每次拿面额最大的 ——> 全局最优：拿走最大数额的钱

题目

10.2 分发饼干

题目链接：

思路

为了满足更多的孩子，就不能造成饼干的浪费。因此，大饼干要尽量分给胃口大的孩子。

在写代码时，先将胃口和饼干大小从高到低排序，然后设置饼干大小的index，遍历孩子胃口，每次比较饼干大小和胃口的大小，如果满足，饼干的index加1，试下一块饼干，如果不满足，那么继续for循环时，去看下一个胃口。

这样使饼干大小保持不变，直到遍历到比它小的胃口，才来到下一个饼干大小。可是如果遍历的是饼干大小，那相当于找寻找一块饼干，使它的size要大于此胃口，可饼干越遍历越小，如果开始不满足，后来也一定不会满足，那么完成for循环后，num还为0。但如果能满足的孩子不为0，总能找到遍历到的一个胃口可以满足那个饼干大小。毕竟遍历的胃口越来越小，总能找到一个合适的胃口满足饼干的大小（如果有的话）。

要注意index超出range的问题。当饼干数量大于胃口数量时，在for循环中，饼干的index可能会加到超过自己的范围，所以在if语句中要同时加上idx的限制（idx<len(s))。我一开始把idx的限制放到了for循环外面一层，但这只能限制一开始进入循环的条件，进去之后，就不会执行最外层操作了。

代码实现

class Solution(object):
    def findContentChildren(self, g, s):
        g.sort(reverse = True)
        s.sort(reverse = True)
        num = 0
        idx = 0
        for i in range(len(g)):
            if idx < len(s) and s[idx] >= g[i]:
                num += 1
                idx += 1              

        return num

376. 摆动序列

题目链接：?https://leetcode.cn/problems/wiggle-subsequence/

思路

统计数组的峰值数量。设定两个变量，preDiff和curDiff，统计当前点和前后的差值。注意当出现峰值时才改变preDiff的值，是考虑到平坡的情况。

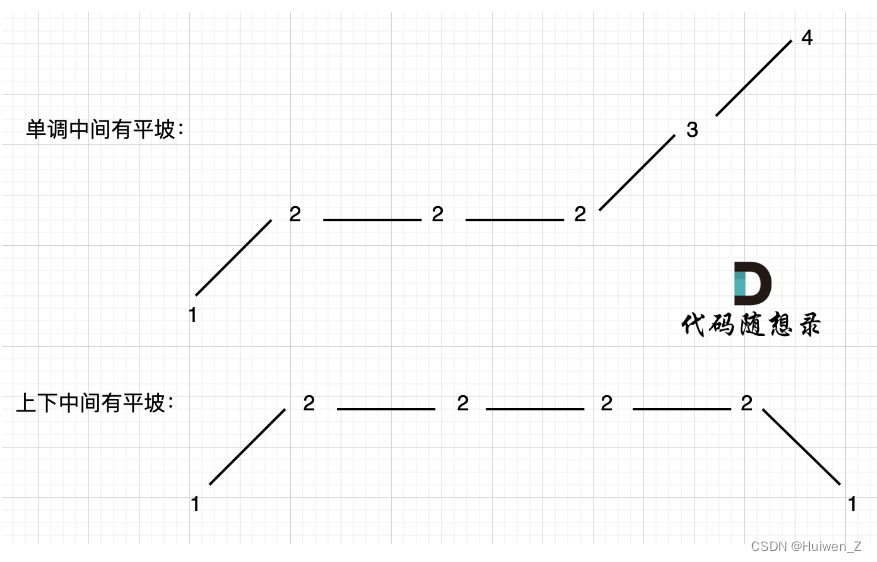
代码实现

class Solution(object):
    def wiggleMaxLength(self, nums):
        result = 1
        preDiff, curDiff = 0, 0

        for i in range(len(nums) - 1):
            curDiff = nums[i+1] - nums[i]
            if (preDiff <= 0 and curDiff > 0) or (preDiff >= 0 and curDiff < 0):
                result += 1
                preDiff = curDiff
        return result
        

53. 最大子序和

思路

局部最优解：从数组开头连续加和，若和大于当前最大和，更新最大值，当加和为负数时，舍弃之前的和，变为0，重新开始加和。注意最大值是负无穷，不要习惯性写0。

代码实现

class Solution(object):
    def maxSubArray(self, nums):
        result = -float('inf')
        sumNum = 0
        i = 0
        while i < len(nums):
            sumNum += nums[i]
            if sumNum > result:
                result = sumNum
            if sumNum < 0:
                sumNum = 0
            i += 1

        return result