HNU-算法设计与分析-实验3

算法设计与分析
实验3

计科210X 甘晴void 202108010XXX

目录

1 用Dijkstra贪心算法求解单源最短路径问题

问题重述

给定一个带权有向图G=(V, E),其中每条边的权是非负实数。另外，给定V中的一个顶点，称为源。现在要计算从源到所有其他各顶点的最短路长度。这里路的长度是指路上各边权之和。（对于无向图的计算可以转化为对有向图的计算）

证明

使用贪心算法完成该题。

输入的带权有向图是G=(V, E)，点集V={1,2, ……,n}，顶点v是源。
c是邻接矩阵，g[i][j]表示边(i,j)的权。 当(i,j)不在E 时，g[i][j]是inf（无穷大）。

dist[i]表示当前从源到顶点i的最短路径长度。

d = min(dist[k]+g[k][u]) (k∈S)

需要证明： dist[u]=d

（1）问题最优解可以以贪心选择开始

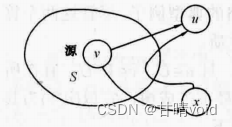
只经过S中的点，计算到V-S中点的特殊最短路径，V-S中选择使得这样的特殊路径最短的一点u，加入S。

证明：集合S初始只含v，选择v直接相连的，边权最短的一点u加入，可以得到最优解。

分析：现在只涉及第一点u，那么只要证明了u得到的路径值是最短的。对于点u：不存在g[v][k]<g[v][u] （k属于S），因此dist[u]=g[v][u]。

因此贪心选择开始可以得到最优解。

（2）最优子结构性质

证明：v到u的最短路径为v-v1-v2-……-vi-u ，那么v-v1-v2-……-vi是v到vi的最短路径。

设v-v1-v2-……-vi的路径长d1，假设存在v到vi的另一条路径是最短路径，长度为d2，满足d2<d1，那么dist[u] = d1 + g[vi][u] < d2+g[vi][u]，矛盾，假设不成立。

问题具有最优子结构性质。

（3）步步贪心选择可以得到最优解

使用数学归纳法进行证明：

令|S|=s（S集合的元素个数为s）

①当s=1时，因为最优解可以由贪心选择开始，成立

②假设s=k时成立，则s=k+1时：

按贪心规则选择V-S中一点u，且只经过S中的点到u的最短路径为d(v , u)，对于所有i∈V-S，知道d(v , u) 是d(v , i)中最小的。

假设u到v的最短路径经过了V-S的点，且经过V-S中第一点为x，因为最优子结构性质，此前的路径长一定为d(v , x)，设x到u的路径长为d’(x , u)
dist[u]=d(v , x) + d’(x , u) < d(v , u) ，因为d’(x , u)>0，所以d(v , x) < d(v , u)，与d(v , u) 是d(v , i)中最小矛盾。

因此s=k时成立，步步贪心可以得到最优解。

（简单来说，若v到S外一点x的距离比v到S外一点u的距离更短，那么x必定得更优先作为下一个扩展的对象，否则就违反了步步贪心的策略，形成了矛盾，反证法。）

模板：Dijkstra算法

1. 声明一个dis的数组来保存源点到其他点的最短路径长度，最开始都设为无穷大，以及一个已经找到最短路径的顶点的集合S。
2. 初始时我们将源点s到源点的路径长度置0，dis[s] = 0,将源点放进集合S中。找到源点所能到达的点（v,w） (v是源点能到的点，w是源点到v点的路长)令dis[v] = w。
3. 接下来从未在集合中的点的dis数值中选出最小的，将这个点加入到集合S中。
4. 接下来要进行判断新加入的结点所能到达的点的路径长度是否小于dis数组中的数值，如果小于，则将dis进行数值更新。
5. 重复3，4操作，直到S中包含了所有点。

图示如下：
（图片来源于网络CSDN大佬）

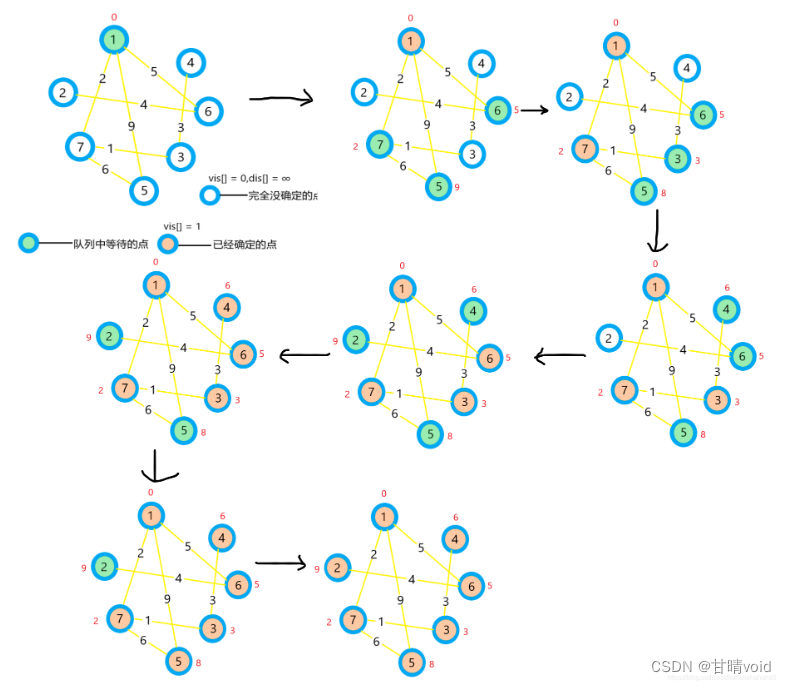
示例读入（因为是按照有向图来做的，所以每条边要读两遍）

7 14
1 7 2
1 5 9
1 6 5
2 6 4
3 4 3
7 3 1
7 5 6
7 1 2
5 1 9
6 1 5
6 2 4
4 3 3
3 7 1
5 7 6

代码

#include <iostream>
#include <cstring>
using namespace std;

const int N = 510;
int n, m;
int g[N][N];// 邻接矩阵
int dist[N];// 距离
bool st[N];// 是否已经确定了最短路径

int dijkstra()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;// 初始化第一个节点
    for(int i = 0; i < n - 1; i++)// 循环n - 1次
    {
        int t = -1;// 找最小节点
        for(int j = 1; j <= n; j++)
        {
            if(!st[j] && (t == -1 || dist[j] < dist[t]))
            {
                t = j;
            }
        }
        st[t] = true;
        // 更新其他节点
        for(int j = 1; j <= n; j++)
        {
            dist[j] = min(dist[j], dist[t] + g[t][j]);
        }
    }
    if(dist[n] == 0x3f3f3f3f) return -1;
    else return 0;
}

int main()
{
    memset(g, 0x3f, sizeof g);
    cin >> n >> m;
    int a, b, c;
    while(m--)
    {
        cin >> a >> b >> c;
        g[a][b] = min(g[a][b], c);
    }
    if (dijkstra()== -1) cout<<"error"<<endl;
    else for(int i = 1; i <= n; i++) cout<<dist[i]<<" ";
    return 0;
}

验证

由于洛谷的单源最短路径问题对算法要求较高（至少得是经过堆优化的Dijkstra），故没有进行在线测评。

就对上面那张图进行验证

示例读入（因为是按照有向图来做的，所以每条边要读两遍）

7 14
1 7 2
1 5 9
1 6 5
2 6 4
3 4 3
7 3 1
7 5 6
7 1 2
5 1 9
6 1 5
6 2 4
4 3 3
3 7 1
5 7 6

运行结果如下

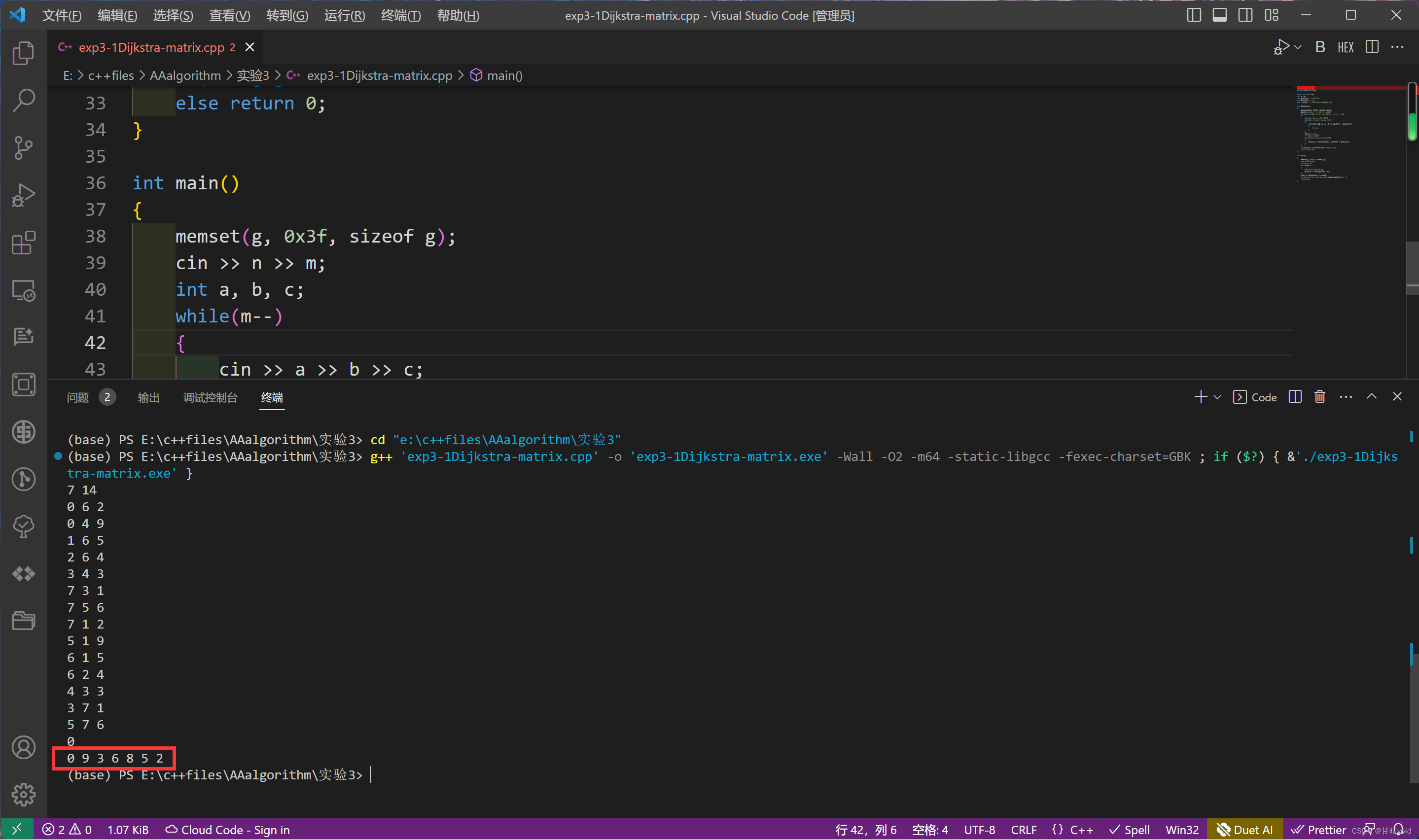
算法分析

时间复杂度O(n^2)，双重循环。

空间复杂度O(n^2)，使用邻接矩阵存储有向图。

1【扩展】 使用堆优化的Dijkstra

原因

如果是稀疏图，使用邻接矩阵存储过于浪费，而且寻找最小边的时候代价太大。故改用优先队列来存储最小的边。

代码

#include <iostream>
#include <cstring>
#include <queue>

using namespace std;

typedef pair<int, int> PII;//分别表示距离和节点

const int N = 150010;

int n, m;

int h[N], e[N], ne[N], w[N], idx;
bool st[N];
int dist[N];

void add(int a, int b, int c)
{
    e[idx] = b;
    w[idx] = c;
    ne[idx] = h[a];
    h[a] = idx++;
}

int dijkstra()
{
    memset(dist, 0x3f, sizeof dist);
    priority_queue<PII, vector<PII>, greater<PII>> pq;
    pq.push({0, 1});
    dist[1] = 0;
    while(pq.size())
    {
        auto t = pq.top();
        pq.pop();
        int node = t.second, val = t.first;
        if(st[node]) continue;
        st[node] = true;
        // 更新其他节点
        for(int i = h[node]; i != -1; i = ne[i])
        {
            int j = e[i];
            dist[j] = min(dist[j], w[i] + dist[node]);
            pq.push({dist[j], j});
        }
    }
    if(dist[n] == 0x3f3f3f3f) return -1;
    else return 0;
}

int main()
{
    memset(h, -1, sizeof h);
    cin >> n >> m;
    int a, b, c;
    while(m--)
    {
        cin >> a >> b >> c;
        add(a, b, c);
    }
    if (dijkstra()== -1) cout<<"error"<<endl;
    else for(int i = 1; i <= n; i++) cout<<dist[i]<<" ";
    return 0;
}

算法分析

二叉堆优化的Dijkstra：

时间复杂度： O( ( V + E )lg V)

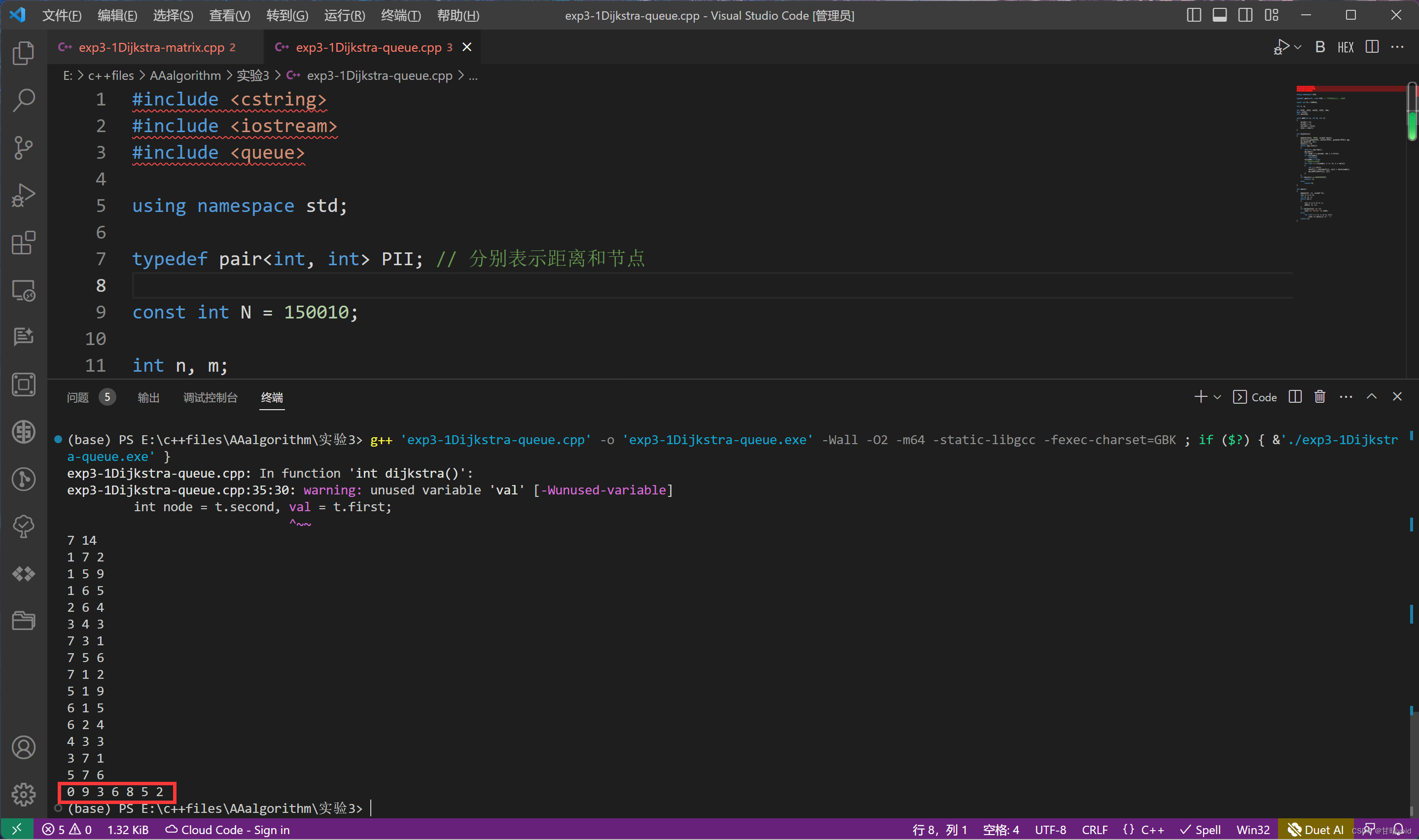
验证

同样就验证上面那张图的解。

2 回溯法求解0-1背包

问题重述

一共有N件物品，第i（i从0开始）件物品的重量为weight[i]，价值为value[i]。在总重量不超过背包承载上限maxw的情况下，求能够装入背包的最大价值是多少？并要求输出选取的物品编号。

（要求使用回溯法求解）

想法

使用回溯法。构造解空间树，从第0层到第n-1层，每层表示对于背包内某个物品的“取”或“不取”。第n层为答案层，在第n层进行判定结果是否是想要的（即能不能获得更优的解），若是就做出相应的处理。

这是一个万能的解空间树图，借来用用。

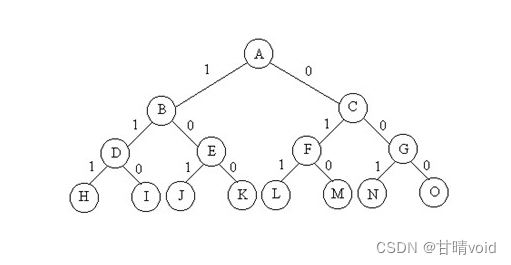
剪枝想法：

（1）如果在第n层之前，就出现了总和大于的maxw情况，那么此时已经超重了。之后无论是否取，都不可能再得到总和小于maxw的结果了。这种情况以及它的子树直接删去即可。

（2）如果在第n层之前，目前已有的价值，即使加上剩余可取的最大价值，也不能达到已经达到的bestv，那么之后即使全部取也不能达到bestv了。这种情况及它的子树直接删去即可。

剪枝代码可以删去，不影响结果，但会降低效率。

代码

// -*- coding:utf-8 -*-

// File    :   01背包问题（回溯）.cpp
// Time    :   2023/12/14
// Author  :   wolf

#include <iostream>
using namespace std;

int w[5000];
int v[5000];
bool flag[5000];
bool ans[5000];
int now_w = 0, now_v = 0;
int n, maxw, bestv = 0;
int rest_v;

void backtrace(int depth)
{
    if (depth == n) // 到达第n层：答案
    {
        if (now_v > bestv && now_w <= maxw) // 答案是需要打印的
        {
            bestv = now_v;
            for (int i = 0; i < n; i++)
            {
                ans[i] = flag[i];
            }
        }
        return;
    }
    if (depth < n && now_w > maxw)
        return; // 剪枝：此时背包已经过重
    if (now_v + rest_v <= bestv)
        return; // 剪枝：此时剩余价值即使全部拾取也无法达到最大价值
    rest_v -= v[depth];
    // 取这个物品
    now_v += v[depth];
    now_w += w[depth];
    flag[depth] = 1;
    backtrace(depth + 1);
    now_v -= v[depth];
    now_w -= w[depth];
    flag[depth] = 0;
    // 不取这个物品
    backtrace(depth + 1);
    rest_v += v[depth];
    return;
}

int main()
{
    cin >> maxw >> n;
    for (int i = 0; i < n; i++)
    {
        cin >> w[i] >> v[i];
        ans[i] = 0;
        flag[i] = 0;
        rest_v += v[i];
    }
    backtrace(0);
    // for (int i = 0; i < n; i++)
    //{
    //     if (ans[i])
    //         cout << i << " ";
    // }
    // cout << endl;
    // cout << "bestv=" << bestv << endl;
    cout << bestv << endl;
    return 0;
}

验证

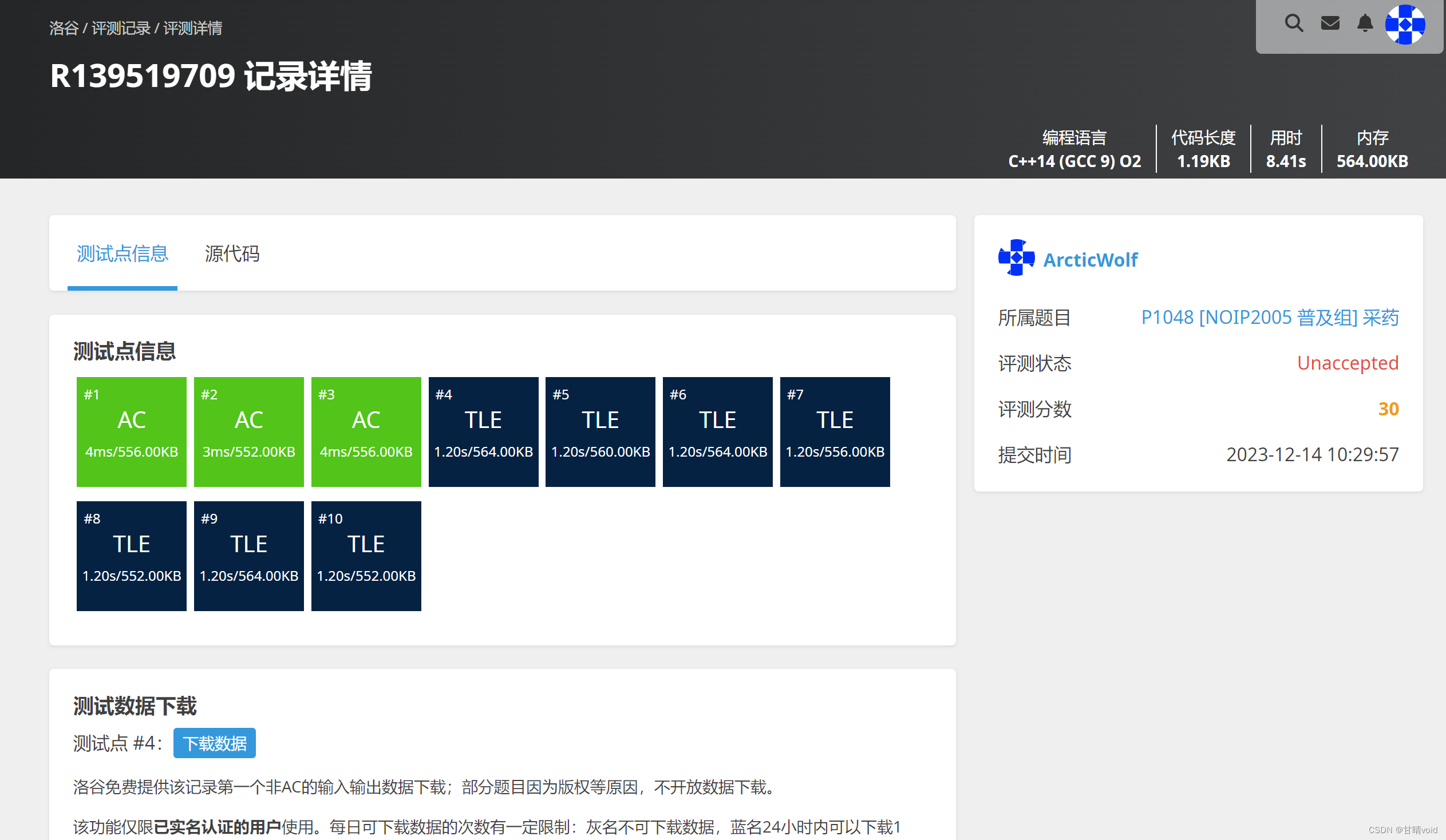
回溯法解决背包问题的O(2^{n)还是从数量级上显著不如动态规划的O(n}2)。

故在数据量很大的时候，不能通过测评，显示超时。

所以01背包问题还是得用动态规划解，本题只是练习一下回溯法。

算法分析

时间复杂度O(2^n)，解空间树是子集树

空间复杂度O(n)，递归深度是n

3 实现题3-17 字符串比较问题

问题重述

【问题描述】
对于长度相同的2 个字符串A和B，其距离定义为相应位置字符距离之和。2 个非空格字符的距离是它们的ASCII码之差的绝对值。空格与空格的距离为0；空格与其它字符的距离为一定值k。
在一般情况下，字符串A和B的长度不一定相同。字符串A的扩展是在A中插入若干空格字符所产生的字符串。在字符串A 和B 的所有长度相同的扩展中，有一对距离最小的扩展，该距离称为字符串A和B的扩展距离。
对于给定的字符串A和B，试设计一个算法，计算其扩展距离。

【算法设计】

对于给定的字符串A和B，编程计算其扩展距离。

【输入样例】

cmc
snmn
2

#第1行是字符串A，第2行是字符串B，第3行是空格与其它字符的距离定值k。

【输出案例】

10

【解释】

c  mc
 snm n

想法

用数组dp[i][j]来记录A,B两串中，A串出到第i个,B串出到第j个，并且把它们出来的部分进行扩展至长度相等后的最小距离。

讨论dp[i][j]时，有以下三种可能

1、A串出一个字符，B串不出字符用空格代替，这样形成的dp[i][j]。则dp[i][j]=dp[i-1][j]+k。

2、A串不出字符用空格代替，B串出一个字符，这样形成的dp[i][j]。则dp[i][j]=dp[i][j-1]+k。

3、A串出一个字符，B串出一个字符。这样形成的dp[i][j]。则dp[i][j]=dp[i-1][j-1]+abs(a[i]-b[j])。

所以状态转移方程为：dp[i][j]=min{dp[i-1][j]+k,dp[i][j-1]+k,dp[i-1][j-1]+abs(a[i]-b[j])}

代码

// -*- coding:utf-8 -*-

// File    :   P1279 字串距离（递归）.cpp
// Time    :   2023/12/13
// Author  :   wolf

#include <iostream>
#include <math.h>
#include <string.h>

using namespace std;

int main()
{
    string A, B;
    int k;
    cin >> A >> B >> k;
    int lenA = A.length();
    int lenB = B.length();
    int dp[lenA + 1][lenB + 1];
    for (int i = 1; i <= lenA; i++)
    {
        dp[i][0] = i * k;
    }
    for (int i = 1; i <= lenB; i++)
    {
        dp[0][i] = i * k;
    }
    dp[0][0] = 0;
    for (int i = 1; i <= lenA; i++)
    {
        for (int j = 1; j <= lenB; j++)
        {
            dp[i][j] = min(dp[i - 1][j - 1] + abs(A[i-1] - B[j-1]), min(dp[i - 1][j] + k, dp[i][j - 1] + k));
            //字符串下标从0开始
        }
    }
    cout << dp[lenA][lenB] << endl;

    return 0;
}

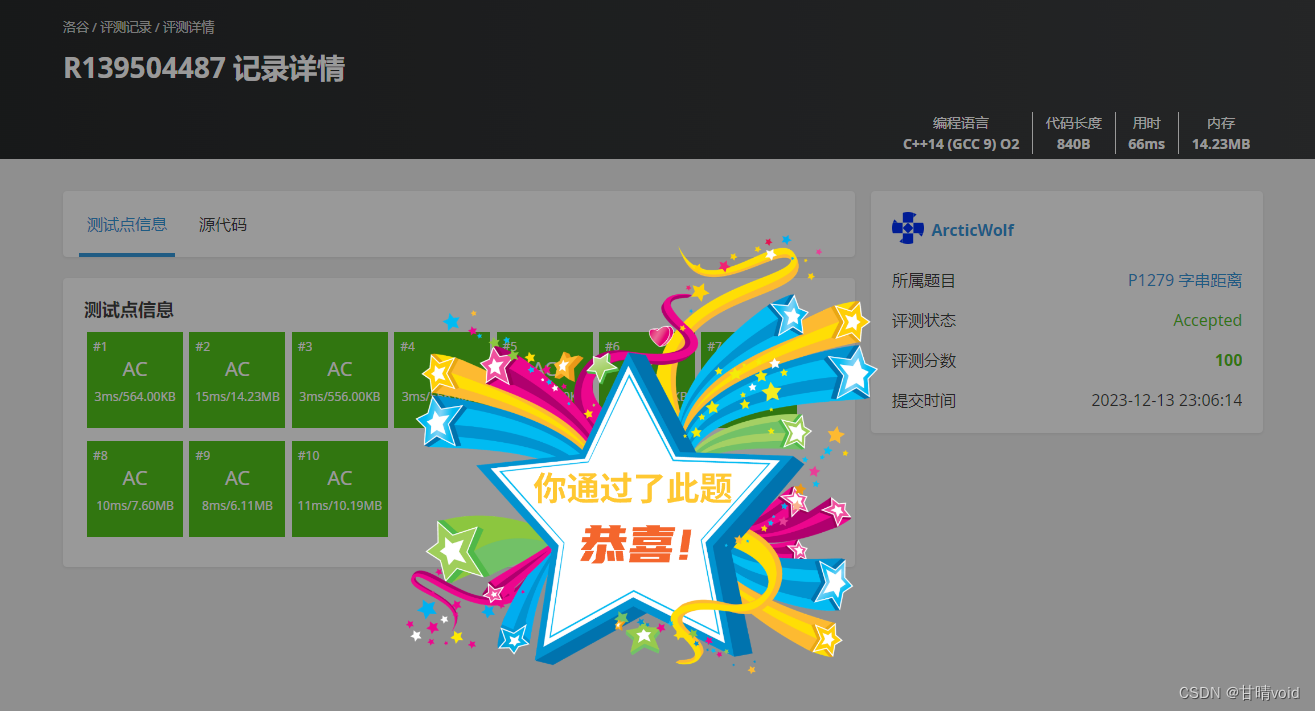
验证

洛谷P1279字串距离

https://www.luogu.com.cn/problem/P1279

测评结果如下：

算法分析

时间复杂度O(nm)，

空间复杂度O(nm)，

4 实现题5-1 子集和问题

问题

【问题描述】
　子集和问题的一个实例为〈S,t〉。其中，S={ x1， x2，…， xn}是一个正整数的集合，c是一个正整数。子集和问题判定是否存在S的一个子集S1，使得子集S1和等于c。
【编程任务】
　　对于给定的正整数的集合S={ x1， x2，…， xn}和正整数c，编程计算S 的一个子集S1，使得子集S1和等于c。
【输入格式】
　　由文件subsum.in提供输入数据。文件第1行有2个正整数n和c，n表示S的个数，c是子集和的目标值。接下来的1 行中，有n个正整数，表示集合S中的元素。
【输出格式】
程序运行结束时，将子集和问题的解输出到文件subsum.out中。当问题无解时，输出“No Solution!”。
【输入样例】
5 10
2 2 6 5 4
【输出样例】
2 2 6

想法

使用回溯法。构造解空间树，从第0层到第n-1层，每层表示对于集合内某个元素的“取”或“不取”。第n层为答案层，在第n层进行判定结果是否是想要的，若是就做出相应的处理。

这是一个万能的解空间树图，借来用用。

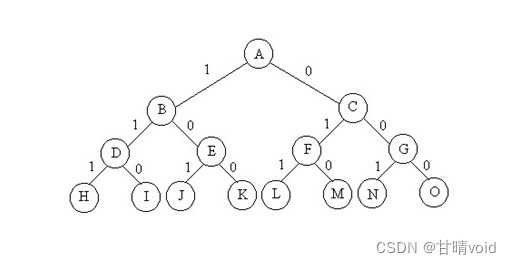
传递是否有解：

使用函数来传递，若返回1则表示已经找到解，返回0表示尚未找到解。若子节点返回1，其父节点都会返回1。

剪枝想法：

如果在第n层之前，就出现了总和大于c的情况，那么之后无论是否取，都不可能再得到总和等于c的结果了。这种情况以及它的子树直接删去即可。

剪枝代码可以删去，不影响结果，但会降低效率。

代码

// -*- coding:utf-8 -*-

// File    :   子集合问题（回溯）.cpp
// Time    :   2023/12/14
// Author  :   wolf

#include <iostream>
using namespace std;

int x[50000];
bool flag[50000];
int total = 0;
int n, c;

int backtrace(int depth)
{
    int if_ans = 0; // 用来存放是否得到了解
    if (depth == n) // 到达第n层：答案
    {
        if (total == c) // 答案是需要打印的
        {
            for (int i = 0; i < n; i++)
            {
                if (flag[i])
                    cout << x[i]<<" ";
            }
            cout << endl;
            return 1;
        }
        return 0;
    }
    if (depth < n && total > c)
        return 0; // 剪枝
    // 取这个数字
    total += x[depth];
    flag[depth] = 1;
    if (backtrace(depth + 1))
        if_ans = 1;
    total -= x[depth];
    flag[depth] = 0;
    // 不取这个数字
    if (backtrace(depth + 1))
        if_ans = 1;
    return if_ans;
}

int main()
{
    cin >> n >> c;
    for (int i = 0; i < n; i++)
    {
        cin >> x[i];
        flag[i] = 0;
    }
    if (!backtrace(0))
        cout << "No Solution!" << endl;
    return 0;
}

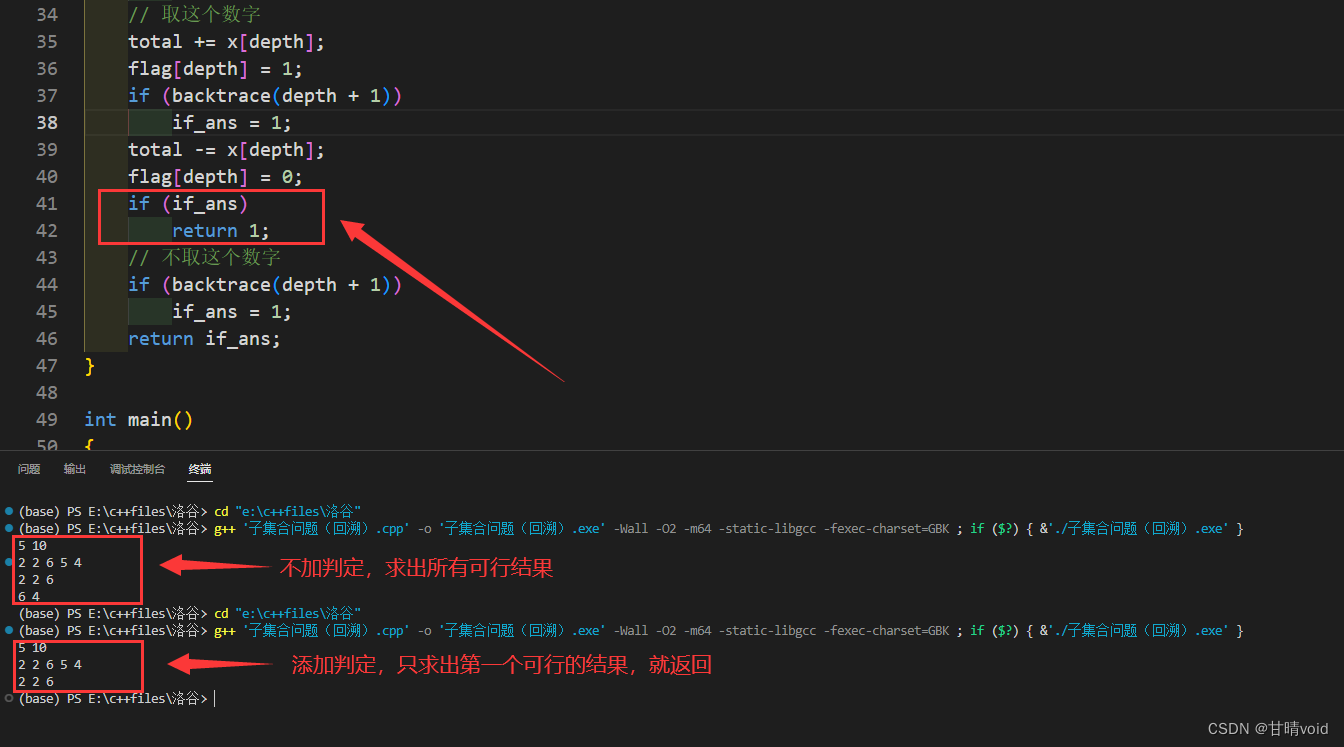
注意，我这个解法给出了所有的结果，如果只需要一个结果，可以稍微修改代码，在递归函数的所有递归入口增加判定，若函数返回值为1，直接返回，不再进入。

【操作】在递归函数第二个递归入口前加这句话

if (if_ans) return 1;

结果就只会出现一个结果。

验证

这道题的原题没有找到线上测评。只能自己给数据试试。

算法分析

时间复杂度O(2^n)，子集树

空间复杂度O(n)，递归深度为n

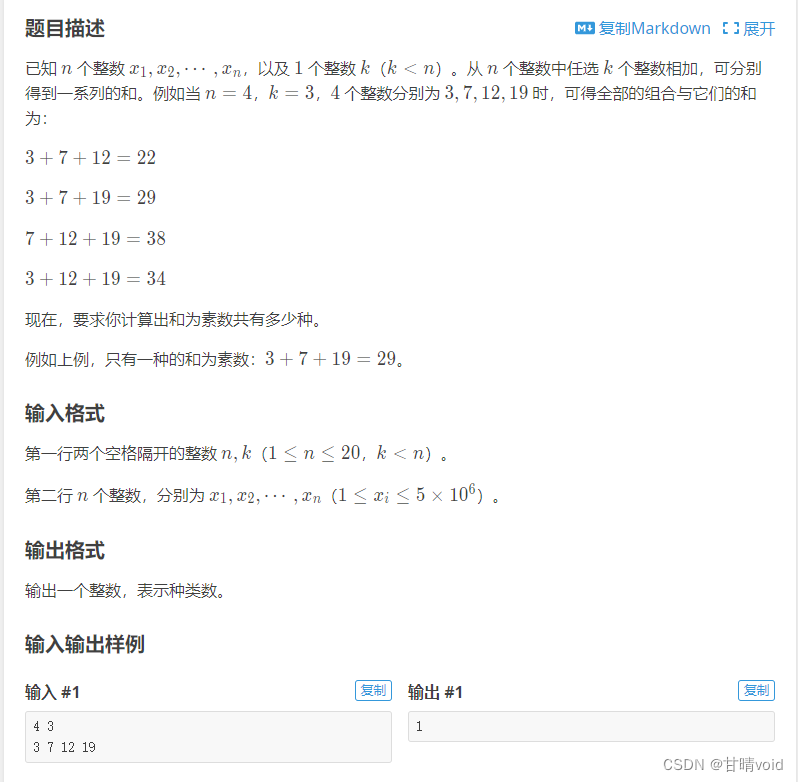
4【扩展】 类似问题：选数

这道题目是类似刚刚上面那道题的，只有一点点小区别：这题是限定取k个整数，而且要判断累加结果是不是素数，比上面那道题要难一点。主要是有测评，所以就做了。

思路极为相似（都是最简单的回溯），所以直接给代码了。

问题

代码

// -*- coding:utf-8 -*-

// File    :   子集合问题（回溯）.cpp
// Time    :   2023/12/14
// Author  :   wolf

#include <iostream>
using namespace std;

int x[50000];
bool flag[50000];
int total = 0;
int n, c;

int backtrace(int depth)
{
    int if_ans = 0; // 用来存放是否得到了解
    if (depth == n) // 到达第n层：答案
    {
        if (total == c) // 答案是需要打印的
        {
            for (int i = 0; i < n; i++)
            {
                if (flag[i])
                    cout << x[i] << " ";
            }
            cout << endl;
            return 1;
        }
        return 0;
    }
    if (depth < n && total > c)
        return 0; // 剪枝
    // 取这个数字
    total += x[depth];
    flag[depth] = 1;
    if (backtrace(depth + 1))
        if_ans = 1;
    total -= x[depth];
    flag[depth] = 0;
    if (if_ans)
        return 1;
    // 不取这个数字
    if (backtrace(depth + 1))
        if_ans = 1;
    return if_ans;
}

int main()
{
    cin >> n >> c;
    for (int i = 0; i < n; i++)
    {
        cin >> x[i];
        flag[i] = 0;
    }
    if (!backtrace(0))
        cout << "No Solution!" << endl;
    return 0;
}

验证

参考文献

Dijkstra证明：https://blog.csdn.net/qq_43496675/article/details/106289566

实验感悟

主要是完成了1道贪心题，2道回溯题，1道动态规划题，题目比较简单，所以做了一些扩展，完成之后感觉还是有点收获的。