Codeforces Round 913 (Div. 3)ABCDEF

A. Rook

题目

题目大意

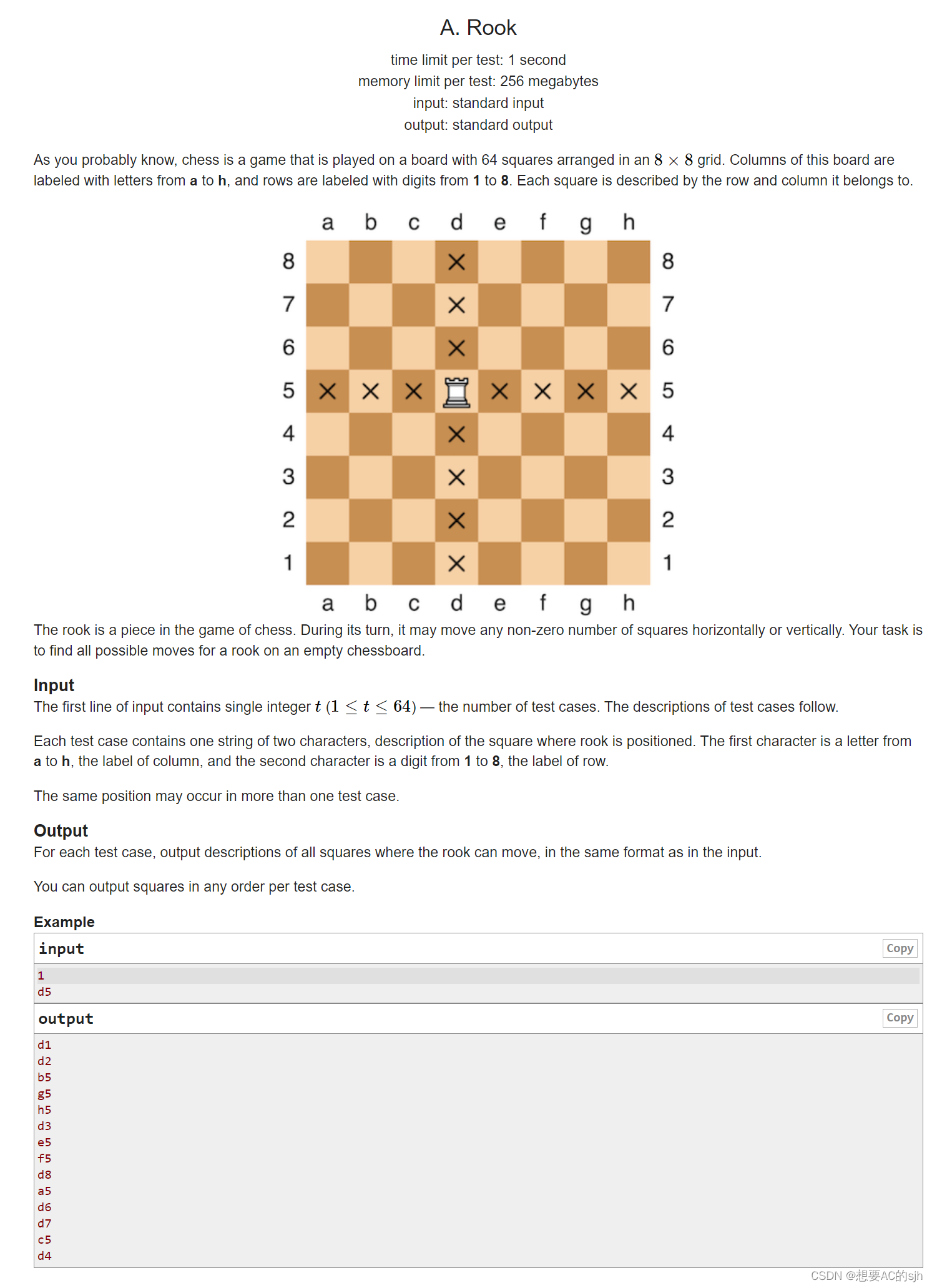
给你一个8*8的棋盘再给你一个棋子的坐标，请你按照任意顺序输出，与这个棋子同一行或者同一列的坐标

思路

直接简单模拟

核心代码

void solve()
{
    char a,b;
    cin>>a>>b;
    int x=a-'a';
    int y=b-'1';
    for(int i=0;i<8;++i)
    {
        for(int j=0;j<8;++j)
        {
            if(x==i&&y==j)continue;
            if(x==i)
            {
                cout<<(char)('a'+i)<<(char)('1'+j)<<"\n";
                continue;
            }
            if(y==j)
            {
                cout<<(char)('a'+i)<<(char)('1'+j)<<"\n";
                continue;
            }
        }
    }
}

B. YetnotherrokenKeoard

题目

题目大意

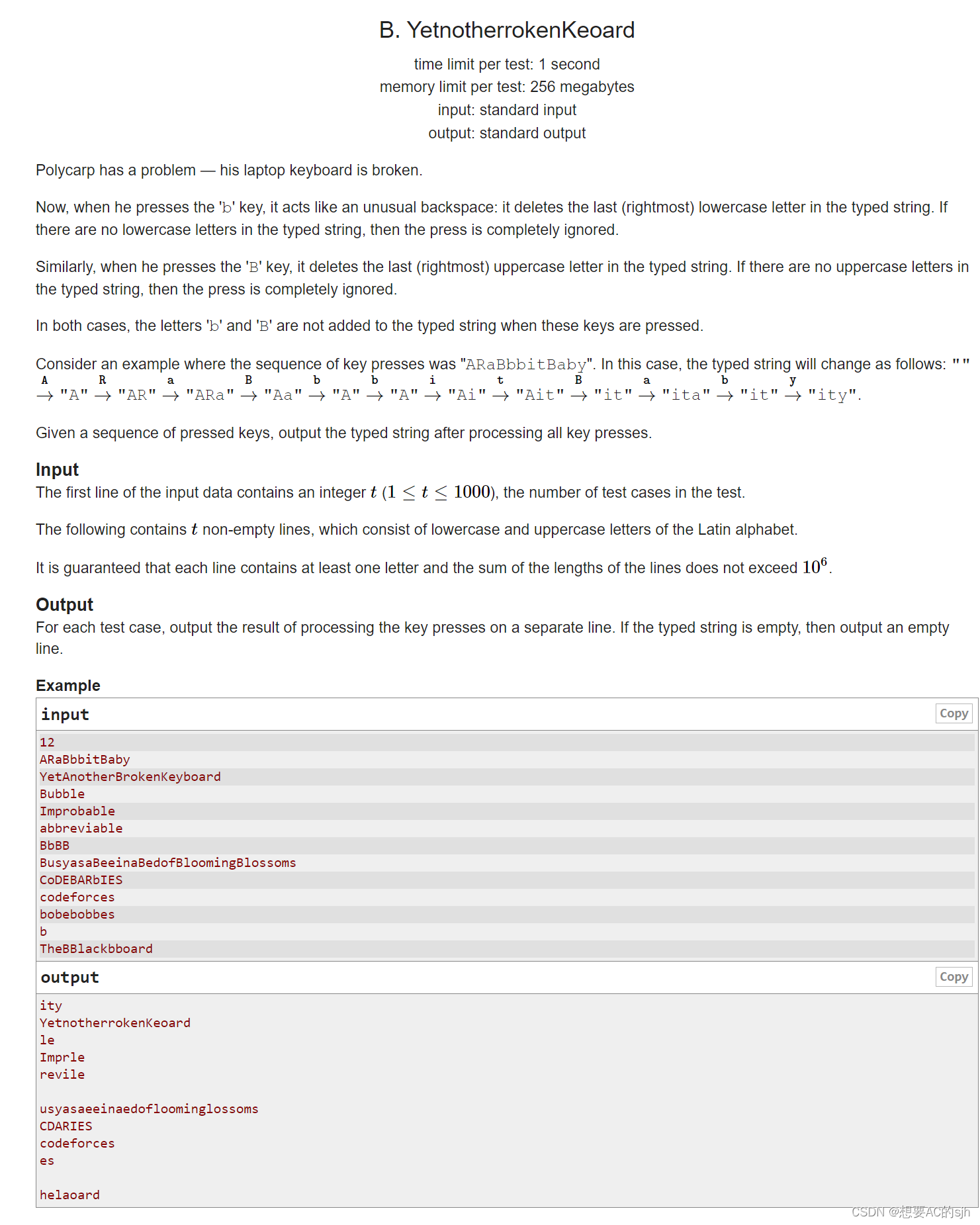
给你给很多个字符串，对于每一个字符串从前往后进行操作，遇到小写字母‘b’的时候去点前面最近的小写字母，遇到大写字母‘B’的时候去掉前面最近的大写字母。

思路

从前面往后面比较难实现，当时我们可以从后面往前面进行操作，如果遇到特殊字母，就记下有多少个字母需要进行处理，最后把答案反过来输出即可

核心代码

void solve()
{
    string s;
    cin>>s;
    int n=s.size();
    int minzhi=0;
    int maxzhi=0;
    vector<char>ans;
    for(int i=n-1;i>=0;--i)
    {
        if(s[i]=='b')
        {
            minzhi++;
            continue;
        }
        else if(s[i]=='B')
        {
            maxzhi++;
            continue;
        }
        else
        {
            if(s[i]>='a'&&s[i]<='z')
            {
                if(minzhi==0)ans.push_back(s[i]);
                else minzhi--;
                continue;
            }
            else if(s[i]>='A'&&s[i]<='Z')
            {
                if(maxzhi==0)ans.push_back(s[i]);
                else maxzhi--;
                continue;
            }
        }
    }
    int len=ans.size();
    if(len==0)
    {
        cout<<"\n";
        return ;
    }
    for(int i=len-1;i>=0;--i)
    {
        cout<<ans[i];
    }
    cout<<"\n";
    return ;
}

C. Removal of Unattractive Pairs

题目

题目大意

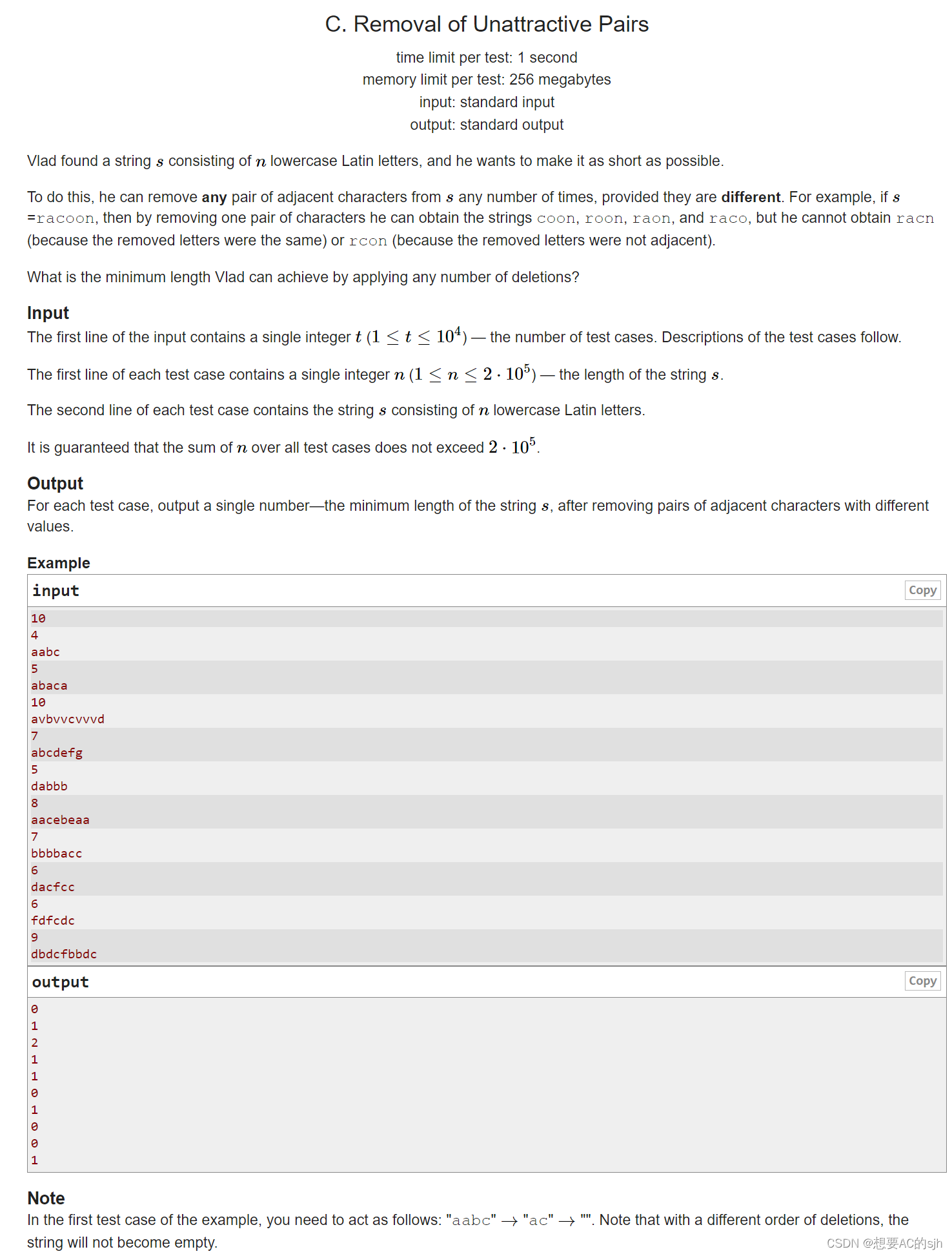
给你很多个字符串，对于每一个字符串，可以进行以下操作：
每一次选择两个相邻两个不同的字母删除
询问最后这个字符串最后的长度最短是多长

思路

首先这个结果和出现次数最多的字母有关，如果最大的那个字母出现次数比其他的字母出现次数总和还要大，那么这个时候最优策略就是所有的字母和最大的相互抵消，最后结果就是出现次数最多的字母出现次数减去其他字母出现次数的总和。
如果最多的那个字母出现次数小于其他的字母出现次数总和，那么这个时候所有的字母都可以想办法进行抵消，此时分为两种情况：第一种字符串总长度是奇数，此时最后一定会留下一个字母；第二种，字符串的总长度是偶数，此时最后不会留下字母。

核心代码

void solve()
{
    int n;
    string s;
    cin>>n>>s;
    int num[26]{};
    for(int i=0;i<n;++i) {
        num[s[i] - 'a']++;
    }
    sort(num,num+26);
    int zhizhen1=0,zhizhen2=25;
    while(zhizhen1<zhizhen2)
    {
        if(num[zhizhen1]<num[zhizhen2])
        {
            num[zhizhen2]-=num[zhizhen1];
            num[zhizhen1]=0;
            zhizhen1++;
        }
        else if(num[zhizhen1]>=num[zhizhen2])
        {
            num[zhizhen1]-=num[zhizhen2];
            num[zhizhen2]=0;
            zhizhen2--;
        }
    }
    int maxzhi=num[25];
    int sum=0;
    for(int i=0;i<25;++i)
    {
        sum+=num[i];
    }
    if(sum<maxzhi)cout<<maxzhi-sum<<"\n";
    else if((sum+maxzhi)%2)cout<<"1\n";
    else cout<<"0\n";
    return ;
}

D. Jumping Through Segments

题目

题目大意

从坐标点0开始出发，每一次最多移动$k$分别给出每一次移动之后的坐标范围
求$k$的最小值

思路

二分查找法

核心代码

E. Good Triples

题目

题目大意

给你一个数字$x$，求满足条件：
1、$a+b+c=x$
2、$a$、$b$、$c$各位数字和等于$x$各位数字和
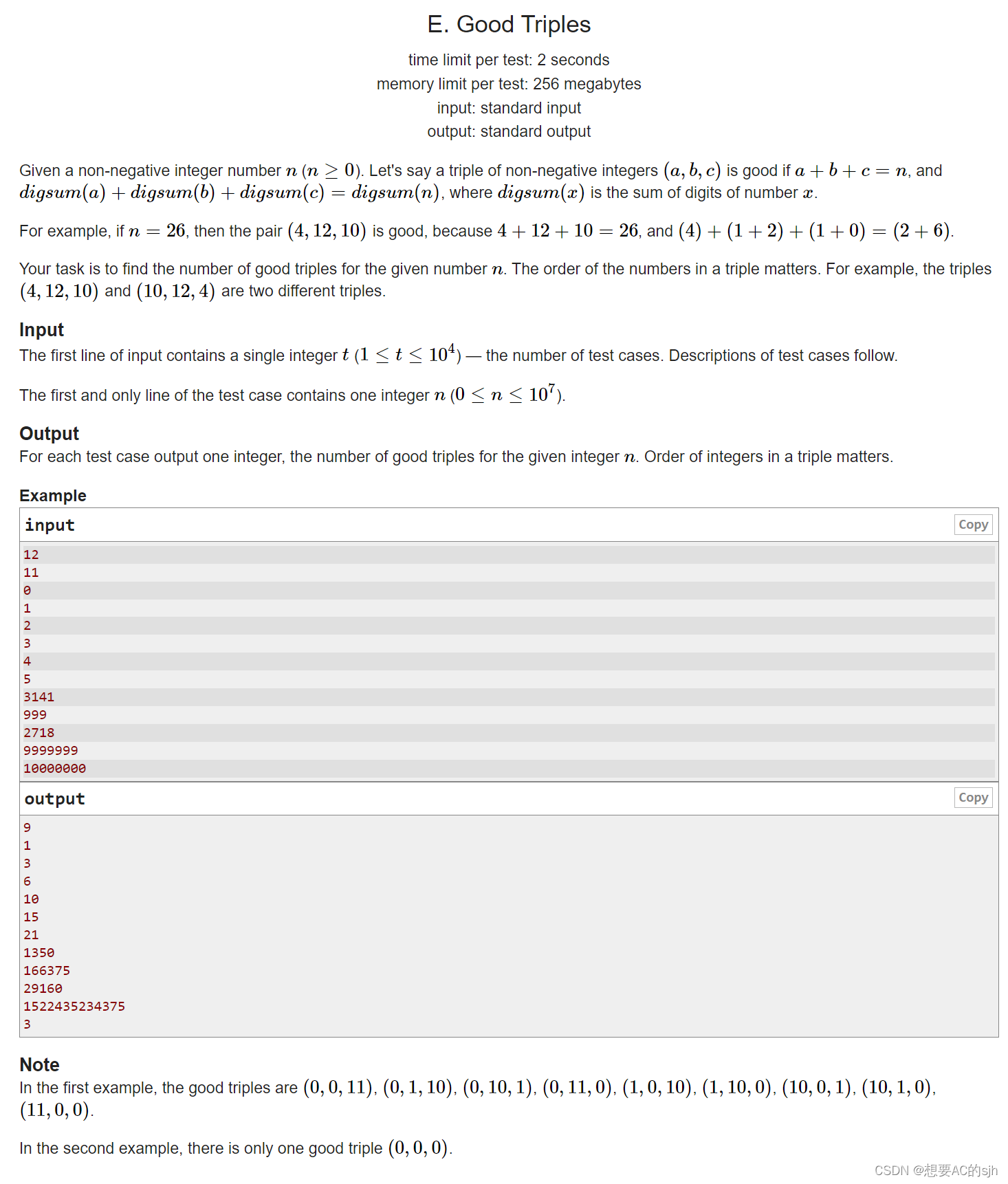
求a、b、c有多少组情况满足条件

思路

简单打表之后发现最后的结果和$x$每一位数字有关，每一位数字对应一个倍数，直接全部相乘即可：
0–1
1–3
2–6
3–10
4–15
5–21
6–28
7–36
8–45
9–55

核心代码

long long a[10]{1,3,6,10,15,21,28,36,45,55};
void solve()
{
    long long n;
    cin>>n;
    long long ans=1;
    long long num;
    while(n>0)
    {
        num=n%10;
        ans*=a[num];
        n/=10;
    }
    cout<<ans<<"\n";
}

F. Shift and Reverse

题目

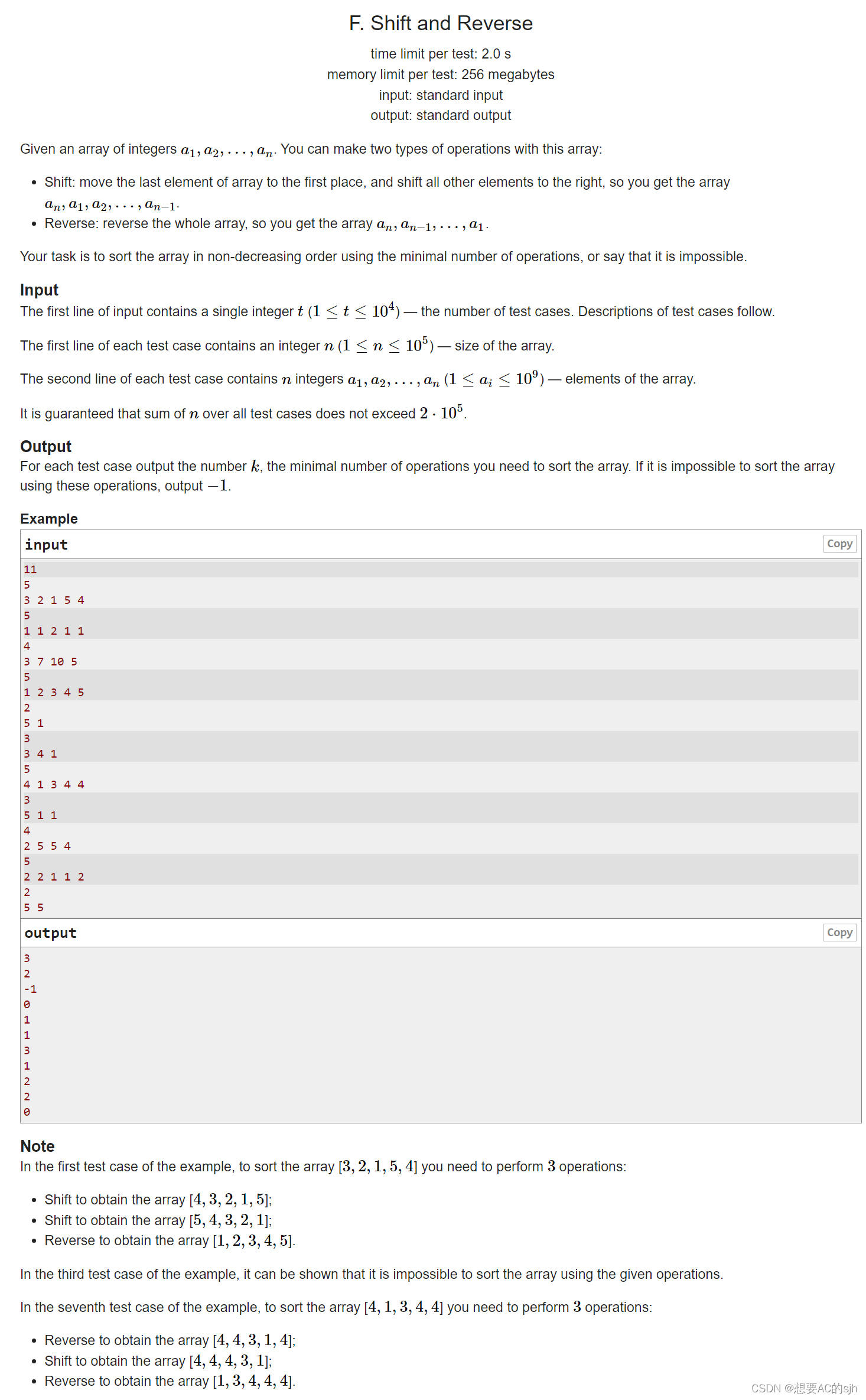
题目大意

有一个数组$a_1,a_2,\dots ,a_n$，你可以通过两个操作使这个数组变为一个升序数组，求操作次数最少的情况
1、把任意“$a_1,a_2,\dots ,a_{n?1},a_n$”变为“$a_n,a_1,a_2,\dots ,a_{n?1}$”
2、把任意“$a_1,a_2,\dots ,a_{n?1},a_n$”变为“$a_n,a_{n?1},\dots ,a_2,a_1$”

思路

有几种情况（大概）：
第一种：不需要进行操作的（从头到尾升序）
第二种：直接进行操作2的
第二种：先进行操作1再进行操作2的
第三种：先进行操作2再进行操作1的
第四种：先1再2再1
第五种：先2再1再2
第六种：无法实现的

核心代码

const int N = 1e5+7;
int a[N];
 
void solve()
{
    int n;
    cin>>n;
    for(int i=0;i<n;++i)
    {
        scanf("%d",&a[i]);
    }
    bool pdsheng=1,pdjiang=1;
    for(int i=1;i<n;++i)
    {
        if(a[i]>a[i-1])pdjiang=0;
        if(a[i]<a[i-1])pdsheng=0;
    }
    if(pdsheng&&pdjiang)
    {
        cout<<"0\n";
        return;
    }
    if(pdjiang==1&&pdsheng==0)
    {
        cout<<"1\n";
        return;
    }
    else if(pdjiang==0&&pdsheng==1)
    {
        cout<<"0\n";
        return;
    }
    int ans1=0,ans2=0;
    //初始正序
    for(;;)
    {
        if(a[0]<a[n-1])
        {
            ans1=-1;
            break;
        }
        int zhizhen1=0,zhizhen2=n-1;
        while(zhizhen1<n&&a[zhizhen1]<=a[zhizhen1+1])zhizhen1++;
        while(zhizhen2>=0&&a[zhizhen2]>=a[zhizhen2-1])zhizhen2--;
//        debug(zhizhen1);
//        debug(zhizhen2);
        if(zhizhen1+1!=zhizhen2)
        {
            ans1=-1;
            break;
        }
        ans1=min(n-zhizhen2,zhizhen1+3);
        break;
    }
    //初始倒序
    for(;;)
    {
        if(a[0]>a[n-1])
        {
            ans2=-1;
            break;
        }
        int zhizhen1=0,zhizhen2=n-1;
        while(zhizhen1<n&&a[zhizhen1]>=a[zhizhen1+1])zhizhen1++;
        while(zhizhen2>=0&&a[zhizhen2]<=a[zhizhen2-1])zhizhen2--;
//        cout<<"***\n";
//        debug(zhizhen1);
//        debug(zhizhen2);
        if(zhizhen1+1!=zhizhen2)
        {
            ans2=-1;
            break;
        }
        ans2=min(n-zhizhen2+1,zhizhen1+2);
//        debug(ans2);
        break;
    }
    if(ans1==-1&&ans2==-1)
    {
        cout<<"-1\n";
        return;
    }
    if(ans1==-1)
    {
        cout<<ans2<<"\n";
        return;
    }
    if(ans2==-1)
    {
        cout<<ans1<<"\n";
        return;
    }
    cout<<min(ans1,ans2)<<"\n";
    return;
}