图形阴影面积-第11届蓝桥杯省赛Python真题精选

[导读]:超平老师的Scratch蓝桥杯真题解读系列在推出之后,受到了广大老师和家长的好评,非常感谢各位的认可和厚爱。作为回馈,超平老师计划推出《Python蓝桥杯真题解析100讲》,这是解读系列的第28讲。
图形阴影面积,本题是2020年6月20日举办的第11届蓝桥杯青少组Python编程省赛编程部分第3题,题目要求编程计算图形的阴影面积。
先来看看题目的要求吧。
一.题目说明
时间限制:4000Ms
内存限制:589824K3
提示信息:
三角形面积公式:S = (ah)/2(公式中a为三角形的底边,h为底边所对应的高)
圆形面积公式:S=πr2(公式中r为圆的半径,π=3.14)
编程实现:
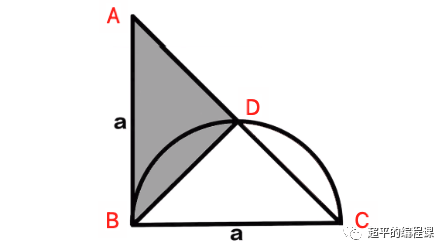
用户输入一个正整数a,作为如图半圆的直径,同时作为如图等腰三角形的直角边长度,求下图的阴影面积,如下所示:

已知条件:
1). 半圆的直径和等腰三角形直角边长度相同;
2). 三角形与半圆部分重叠;
3). 三角形为等腰直角三角形;
输入描述:
一个正整数(作为圆的直径)
输出描述:
图形阴影面积(保留2位小数)
样例输入:
10
样例输出:
25.00
评分标准:
-
20分:能正确输出一组数据;
-
20分:能正确输出两组数据;
-
20分:能正确输出三组数据;
-
20分:能正确输出四组数据。
二.思路分析
由于这里涉及到圆弧,直接计算需要特定的公式,但题目并没有提供弧形面积的计算公式,所以需要换个思路。
为了方便描述,我们在图形上标注A、B、C个点,并添加辅助线DE,如图:

仔细观察上图,我们可以发现,以DE为轴,左边的1/4圆BDE和右边的1/4圆CDE是完全对称的,三角形BDE和三角形CDE也是完全对称的。
由此可以得知,圆弧BD和圆弧CD是完全对称且相等的,所以,我们可以直接将上面的图形转换如下:
实际上,只需要计算三角形ABD的面积就可以了,由于ABC是一个等腰直接三角形,所以ABD的面积刚好是ABC的一半,问题也就迎刃而解了。
思路有了,接下来,我们就进入具体的编程实现环节。
三.编程实现
根据上面的思路分析,我们直接编写程序如下:

代码比较简单,强调一点,输出的时候需要保留两位小数,这里使用了格式符%.2f。
测试程序,输入10,结果如下:
![]()
输入18,结果如下:
![]()
至此,整个程序就全部完成了,你也可以输入不同的数字来测试效果。
四.总结与思考
本题的分数为80分,代码只有短短的3行,涉及到的知识点包括:
-
输入输出处理;
-
算术运算;
-
格式化输出;
题目比较简单,代码也非常少,关键是要仔细观察并分析图形的特点,找到最简单的方案。题目给出了计算圆的面积公式,可不要被它干扰了。
实际上,在平时学习的过程中,遇到任何一道题,我们都要找出如下三种信息,已知信息、隐含信息和干扰信息。所以说,审好题是解决问题的第一步,也是最关键的一步。
你还有什么好的想法和创意吗,也非常欢迎和超平老师分享探讨。
如果你觉得文章对你有帮助,别忘了点赞和转发,予人玫瑰,手有余香😄
需要源码的,可以移步至“超平的编程课”gzh。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- vue2 methods 下的init()是固定写法么?属于初始化么,怎么理解这个方法呢
- 基于单片机的室内空气质量检测系统设计与实现
- 服务器管理平台(6)- Utils
- 【MIMO 从入门到精通】[P6]【What is Beamforming?】
- C#设计模式教程(13):代理模式
- 92. 反转链表 II
- 100天精通鸿蒙从入门到跳槽——第12天:ArkTS基本语法入门
- Redis 面试题 | 05.精选Redis高频面试题
- [PyTorch][chapter 8][李宏毅深度学习][Back propagation]
- Windows 2012 R2 单网卡安装 PPTPVP*