【二叉树的顺序结构及实现一-堆】

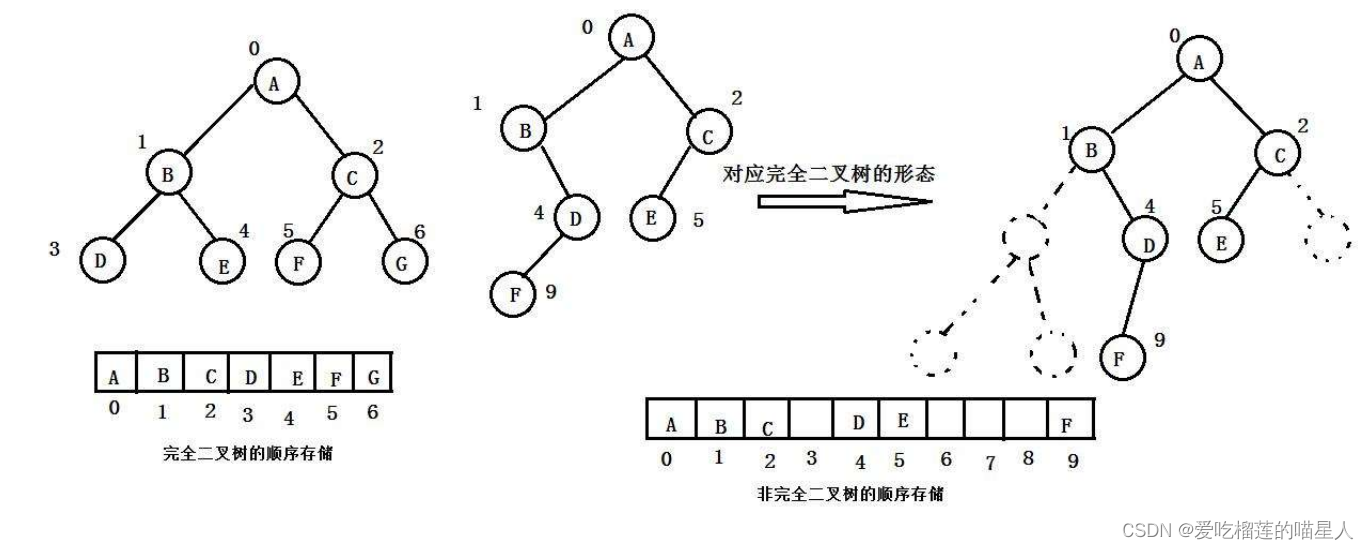
一、二叉树的顺序结构

普通的二叉树是不适合用数组来存储的，因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结构存储。现实中我们通常把堆(一种二叉树)使用顺序结构的数组来存储，需要注意的是这里的堆和操作系统虚拟进程地址空间中的堆是两回事，一个是数据结构，一个是操作系统中管理内存的一块区域分段。

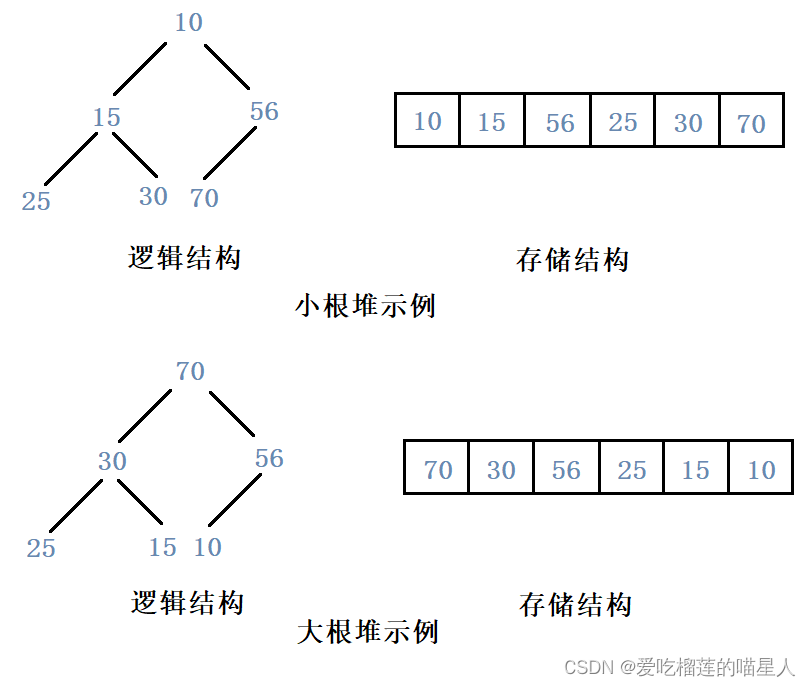
二、堆的概念及结构

如果有一个关键码的集合 k = { k 0 , k 1 , k 2 , . . . , k n ? 1 } , k=\left \{k_{0},k_{1},k_{2},...,k_{n-1} \right \}, k={k0?,k1?,k2?,...,kn?1?},把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中，并满足：$$K_i?K_{2?i+1}且K_i?K_{2?i+2}\left(K_i?K_{2?i+1}且K_i?K_{2?i+2}\right)i=0,1,\mathrm{2...},$$则称为小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。
堆的性质：

• 堆中某个节点的值总是不大于或不小于其父节点的值；
• 堆总是一棵完全二叉树。
  

三、堆的实现(以小堆为例)

1、堆的结构体

typedef int HPDataType;
typedef struct Heap
{
	HPDataType* a;
	int size;
	int capacity;
}HP;

2、堆的初始化->void HeapInit(HP* hp);

void HeapInit(HP* hp)
{
	assert(hp);
	hp->a = NULL;
	hp->size = hp->capacity = 0;
}

3、堆的销毁->void HeapDestroy(HP* hp);

void HeapDestroy(HP* hp)
{
	assert(hp);
	free(hp->a);
	hp->capacity = hp->size = 0;
}

4、堆的判空->bool HeapEmpty(HP* hp);

bool HeapEmpty(HP* hp)
{
	assert(hp);
	return hp->size == 0;
}

5、取堆顶的数据->HPDataType HeapTop(HP* hp);

HPDataType HeapTop(HP* hp)
{
	assert(hp);
	assert(!HeapEmpty(hp));
	return hp->a[0];
}

6、堆的数据个数->int HeapSize(HP* hp);

int HeapSize(HP* hp)
{
	assert(hp);
	return hp->size;
}

7、交换函数->void Swap(HPDataType* px, HPDataType* py);

void Swap(HPDataType* px, HPDataType* py)
{
	HPDataType tmp = *px;
	*px = *py;
	*py = tmp;
}

8、堆的打印->void HeapPrint(HP* hp);

void HeapPrint(HP* hp)
{
	for (int i = 0; i < hp->size; ++i)
	{
		printf("%d ", hp->a[i]);
	}
	printf("\n");
}

9、堆向上调整算法->void AdjustUp(int* a, int child);

void AdjustUp(int* a, int child)
{
	assert(a);
	int parent = (child - 1) / 2;
	while (child > 0)
	{
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);

			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

10、堆的插入->void HeapPush(HP* hp, HPDataType x);

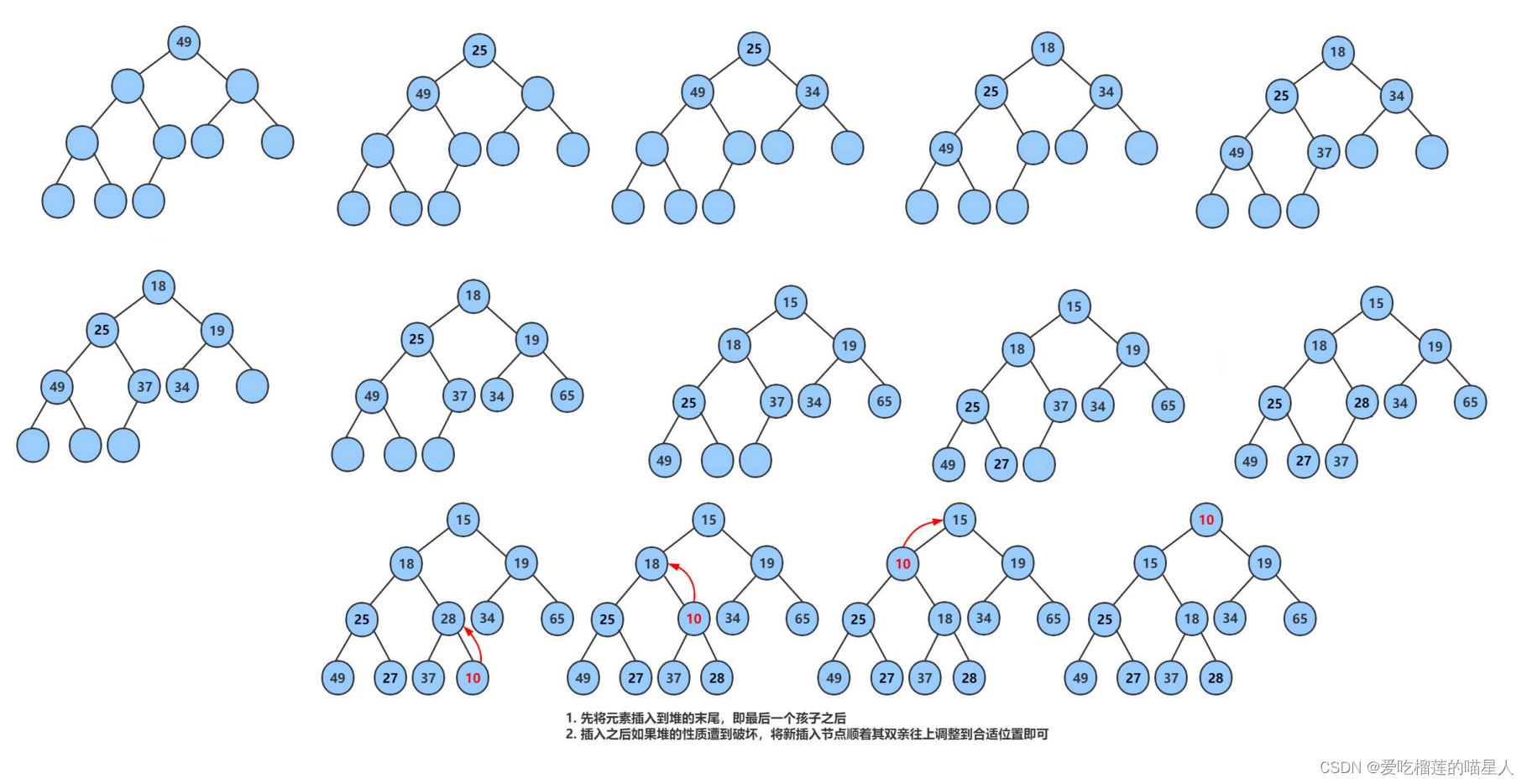
void HeapPush(HP* hp, HPDataType x)
{
	assert(hp);
	if (hp->size == hp->capacity)
	{
		size_t newCapacity = hp->capacity == 0 ? 4 : hp->capacity * 2;
		HPDataType* tmp = realloc(hp->a, sizeof(HPDataType) * newCapacity);
		if (tmp == NULL)
		{
			printf("realloc fail\n");
			exit(-1);
		}
		hp->a = tmp;
		hp->capacity = newCapacity;
	}
	hp->a[hp->size] = x;
	hp->size++;
	AdjustUp(hp->a, hp->size - 1);
}

结合9、10的例子：

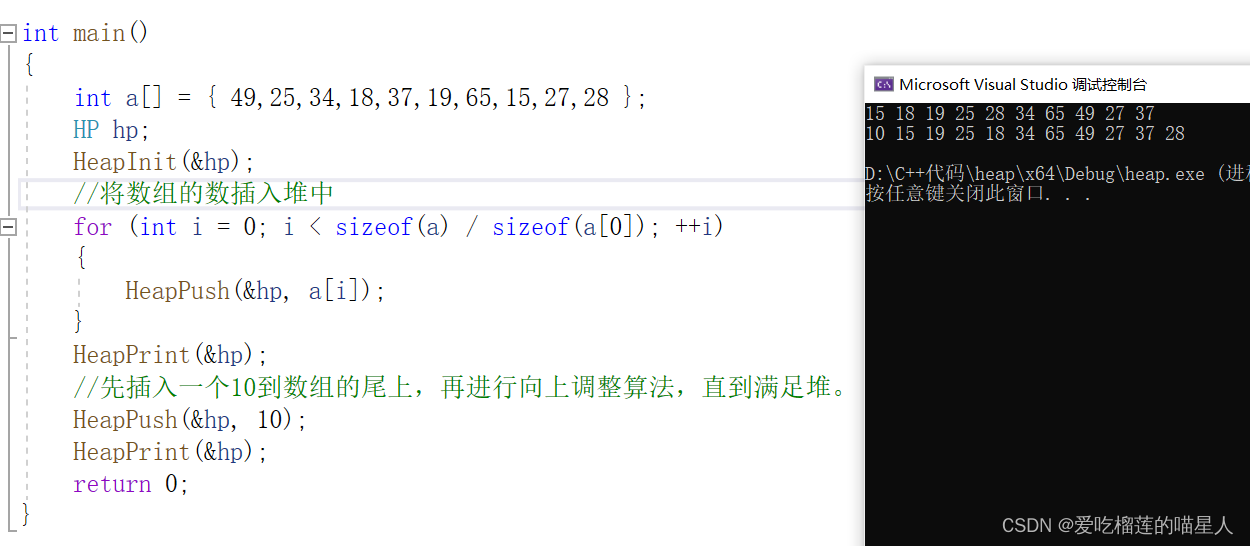
int main()
{
	int a[] = { 49,25,34,18,37,19,65,15,27,28 };
	HP hp;
	HeapInit(&hp);
	//将数组的数插入堆中
	for (int i = 0; i < sizeof(a) / sizeof(a[0]); ++i)
	{
		HeapPush(&hp, a[i]);
	}

	HeapPrint(&hp);
	//先插入一个10到数组的尾上，再进行向上调整算法，直到满足堆。
	HeapPush(&hp, 10);
	HeapPrint(&hp);
	return 0;
}

运行结果：

代码详解：

11、堆向下调整算法->void AdjustDown(int* a, int n, int parent);

向下调整算法有一个前提：左右子树必须是一个堆，才能调整。

void AdjustDown(int* a, int n, int parent)
{
	int child = parent * 2 + 1;
	while (child < n)
	{
		// 选出左右孩子中小的那一个
		if (child + 1 < n && a[child + 1] < a[child])
		{
			++child;
		}

		// 如果小的孩子小于父亲，则交换，并继续向下调整
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

12、堆的删除->void HeapPop(HP* hp);

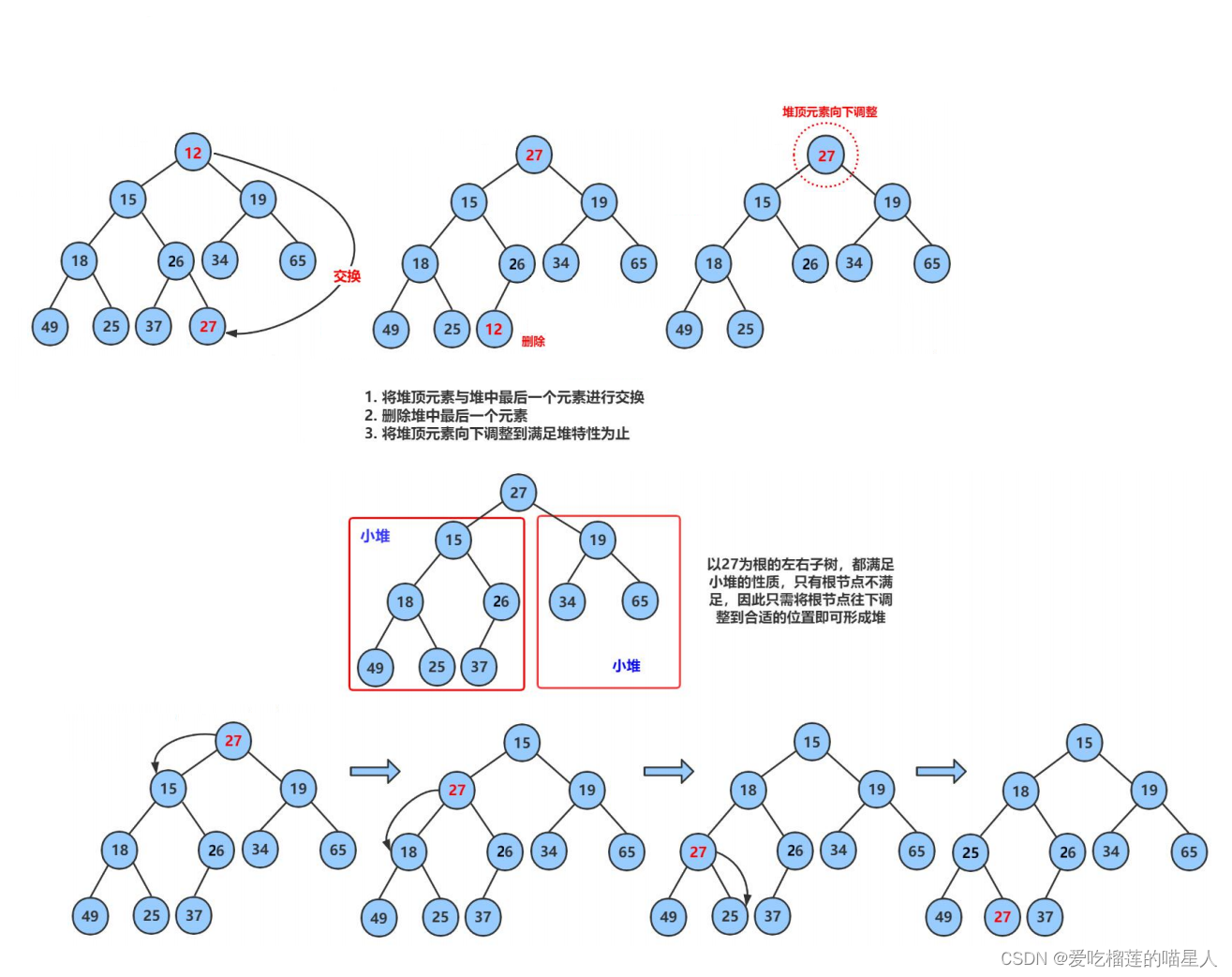
删除堆是删除堆顶的数据，将堆顶的数据根最后一个数据一换，然后删除数组最后一个数据，再进行向下调整算法。

void HeapPop(HP* hp)
{
	assert(hp);
	assert(!HeapEmpty(hp));
	Swap(&hp->a[0], &hp->a[hp->size - 1]);
	hp->size--;
	AdjustDown(hp->a, hp->size, 0);
}

结合11、12例子：

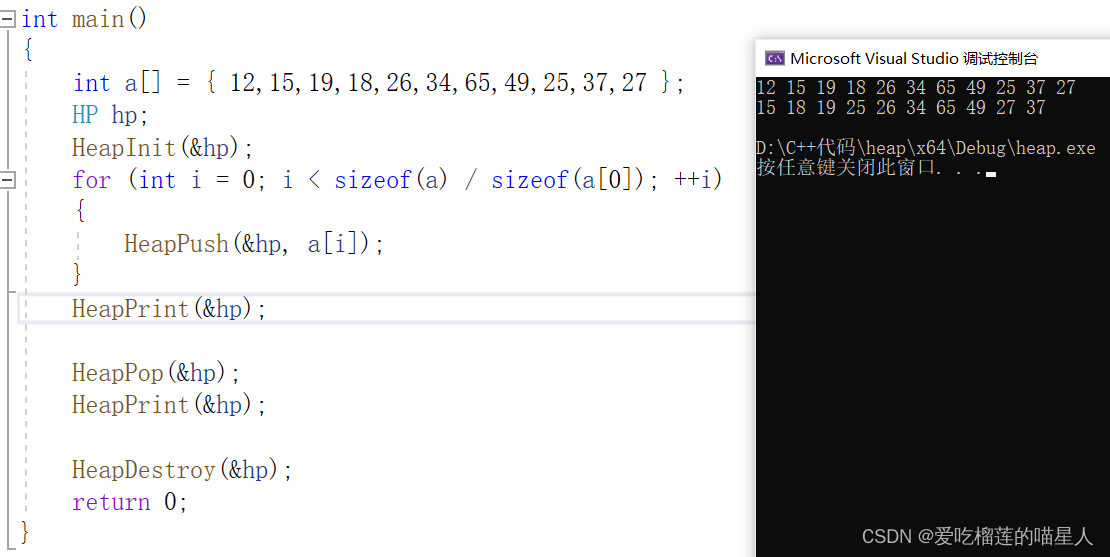
int main()
{
	int a[] = { 12,15,19,18,26,34,65,49,25,37,27 };
	HP hp;
	HeapInit(&hp);
	for (int i = 0; i < sizeof(a) / sizeof(a[0]); ++i)
	{
		HeapPush(&hp, a[i]);
	}
	HeapPrint(&hp);
	//删除堆顶元素
	HeapPop(&hp);
	HeapPrint(&hp);
	HeapDestroy(&hp);
	return 0;
}

运行结果：

代码详解：

四、堆的应用

1、 堆排序

堆排序即利用堆的思想来进行排序，总共分为两个步骤：
1)、建堆：
升序：建大堆
降序：建小堆
2). 利用堆删除思想来进行排序
建堆和堆删除中都用到了向下调整，因此掌握了向下调整，就可以完成堆排序。
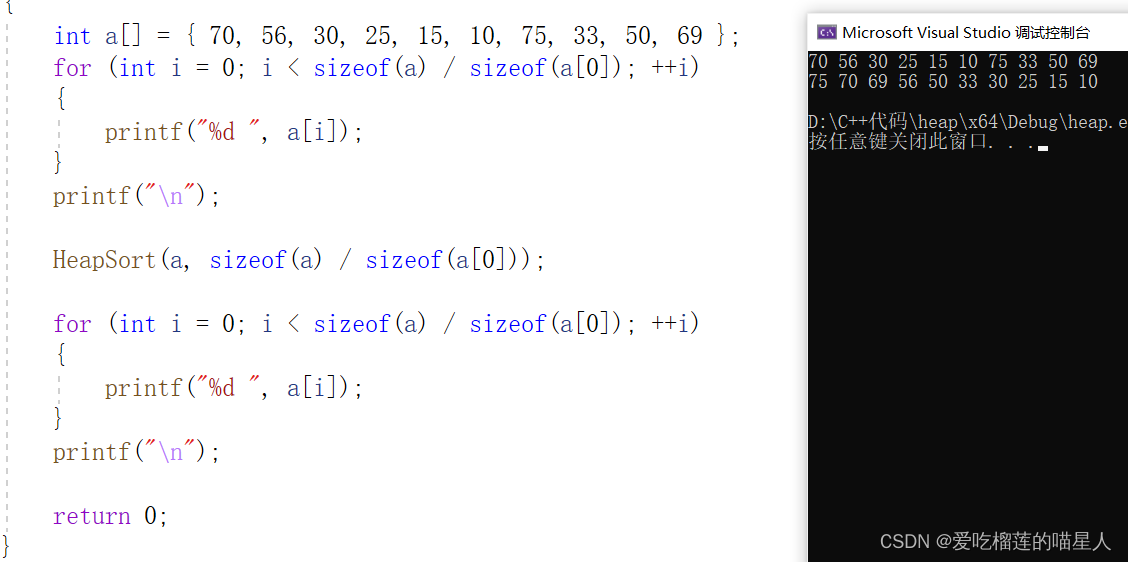
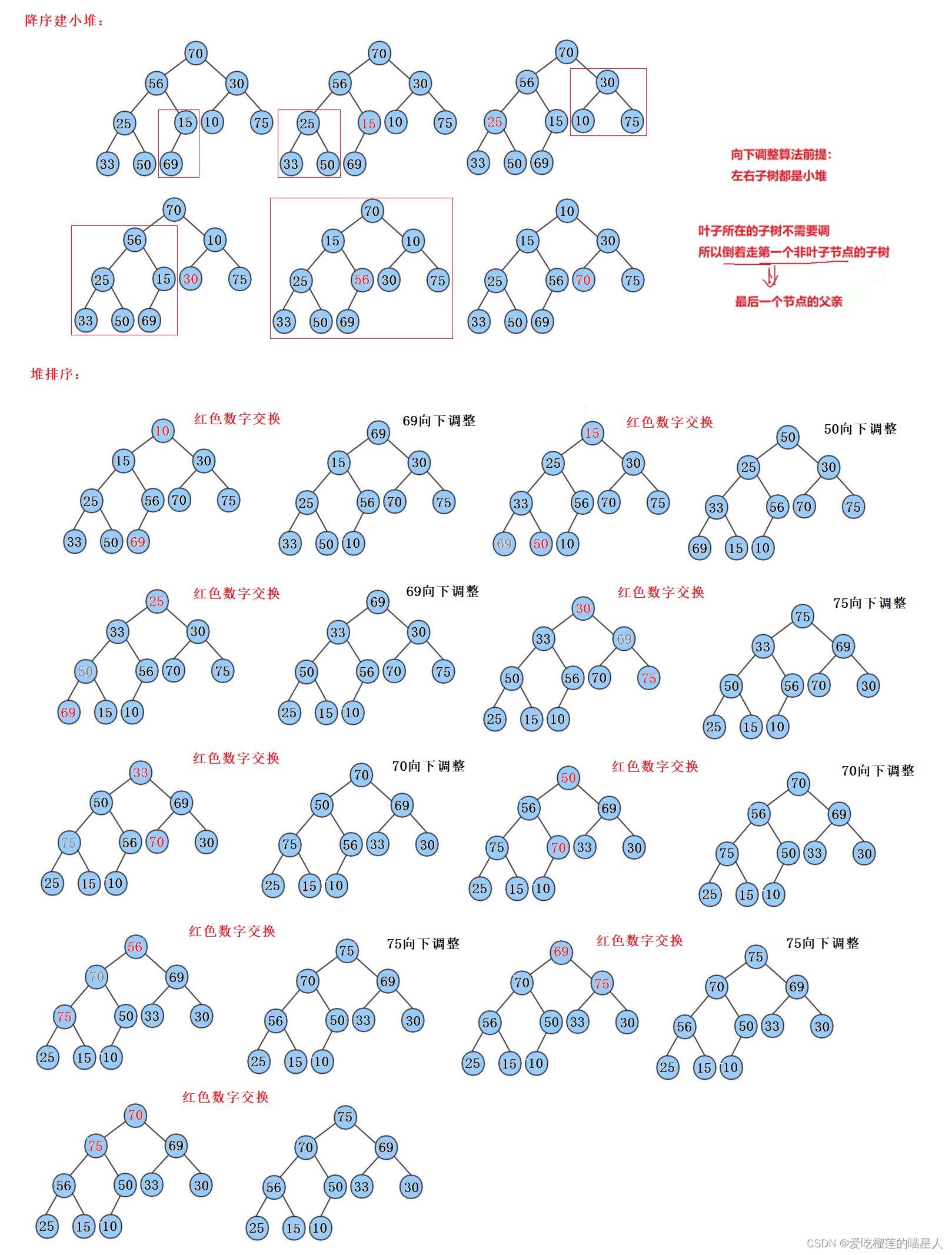
3)、例子：

void AdjustDown(int* a, int n, int parent)
{
	int child = parent * 2 + 1;
	while (child < n)
	{
		// 选出左右孩子中小的那一个
		if (child + 1 < n && a[child + 1] < a[child])
		{
			++child;
		}

		// 如果小的孩子小于父亲，则交换，并继续向下调整
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}
void HeapSort(int* a, int n)
{
	//下面我们给出一个数组，这个数组逻辑上可以看做一颗完全二叉树，但是还不是一个堆，现在我们通过算
	法，把它构建成一个堆。根节点左右子树不是堆，我们怎么调整呢？这里我们从倒数的第一个非叶子节点的
	子树开始调整，一直调整到根节点的树，就可以调整成堆。
 	//O(N)建小堆，降序
	for (int i = (n - 1 - 1) / 2; i >= 0; --i)
	{
		AdjustDown(a, n, i);
	}

	//依次选数，调堆
	//O(N*logN)
	for (int end = n - 1; end > 0; --end)
	{
		Swap(&a[end], &a[0]);

		//再调堆，选出次小的数
		AdjustDown(a, end, 0);
	}
}

int main()
{
	int a[] = { 70, 56, 30, 25, 15, 10, 75, 33, 50, 69 };
	for (int i = 0; i < sizeof(a) / sizeof(a[0]); ++i)
	{
		printf("%d ", a[i]);
	}
	printf("\n");

	HeapSort(a, sizeof(a) / sizeof(a[0]));

	for (int i = 0; i < sizeof(a) / sizeof(a[0]); ++i)
	{
		printf("%d ", a[i]);
	}
	printf("\n");

	return 0;
}

4)、运行结果

5)、详解例子建堆和排序

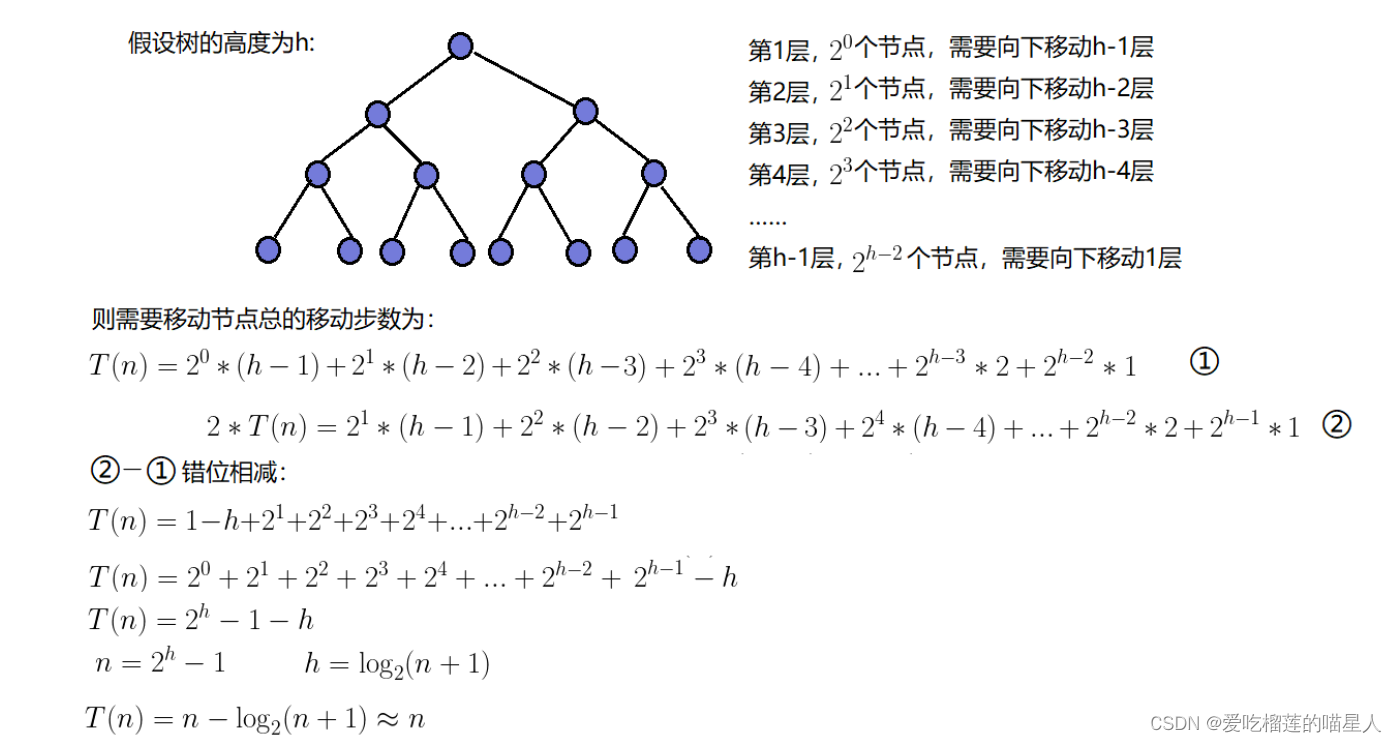
6)、建堆时间复杂度
因为堆是完全二叉树，而满二叉树也是完全二叉树，此处为了简化使用满二叉树来证明(时间复杂度本来看的
就是近似值，多几个节点不影响最终结果):

因此：建堆的时间复杂度为O(N)。

2、TOP-K问题

TOP-K问题：即求数据结合中前K个最大的元素或者最小的元素，一般情况下数据量都比较大。
对于Top-K问题，能想到的最简单直接的方式就是排序，但是：如果数据量非常大，排序就不太可取了(可能数据都不能下子全部加载到内存中)。最佳的方式就是用堆来解决，基本思路如下：
1. 用数据集合中前K个元素来建堆

• 前k个最大的元素，则建小堆
• 前k个最小的元素，则建大堆

2. 用剩余的N-K个元素依次与堆顶元素来比较，不满足则替换堆顶元素,将剩余N-K个元素依次与堆顶元素比完之后，堆中剩余的K个元素就是所求的前K个最小或者最大的元素。
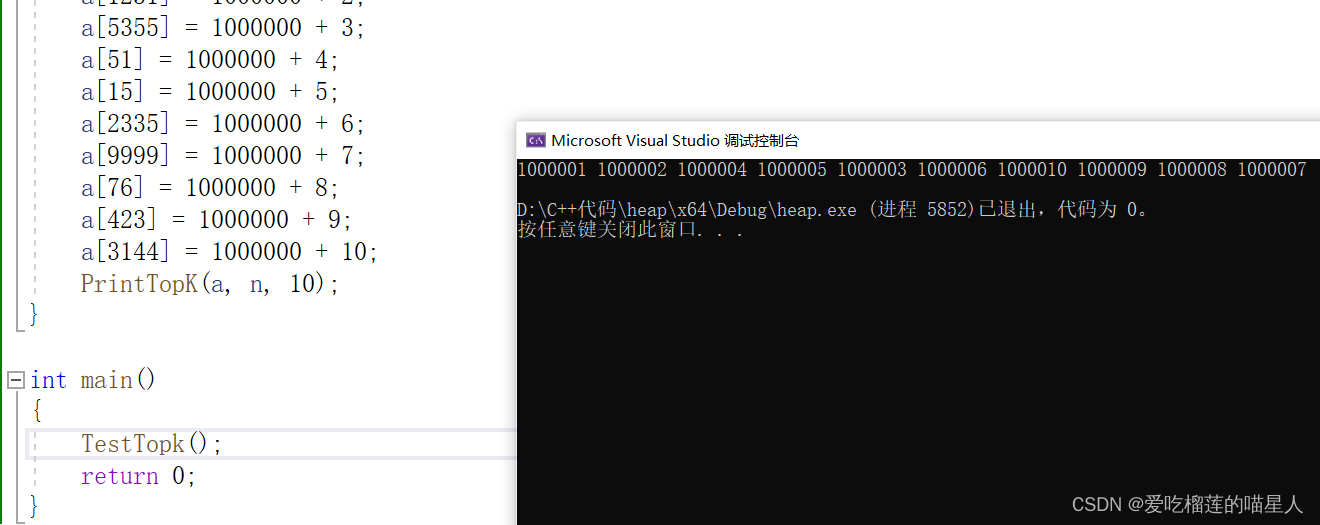
3、例子：

// 在N个数找出最大的前K个  or  在N个数找出最小的前K个
void PrintTopK(int* a, int n, int k)
{
	HP hp;
	HeapInit(&hp);
	// 创建一个K个数的小堆
	for (int i = 0; i < k; ++i)
	{
		HeapPush(&hp, a[i]);
	}

	// 剩下的N-K个数跟堆顶的数据比较，比他大，就替换他进堆
	for (int i = k; i < n; ++i)
	{
		if (a[i] > HeapTop(&hp))
		{
			HeapPop(&hp);
			HeapPush(&hp, a[i]);
			//hp.a[0] = a[i];
			//AdjustDown(hp.a, hp.size, 0);
		}
	}

	HeapPrint(&hp);

	HeapDestroy(&hp);
}

void TestTopk()
{
	int n = 1000000;
	int* a = (int*)malloc(sizeof(int) * n);
	srand(time(0));
	for (size_t i = 0; i < n; ++i)
	{
		a[i] = rand() % 1000000;
	}
	// 再去设置10个比100w大的数
	a[5] = 1000000 + 1;
	a[1231] = 1000000 + 2;
	a[5355] = 1000000 + 3;
	a[51] = 1000000 + 4;
	a[15] = 1000000 + 5;
	a[2335] = 1000000 + 6;
	a[9999] = 1000000 + 7;
	a[76] = 1000000 + 8;
	a[423] = 1000000 + 9;
	a[3144] = 1000000 + 10;
	PrintTopK(a, n, 10);
}

int main()
{
	TestTopk();
	return 0;
}

4、运行结果：

以上是本篇文章的全部内容，如果文章有错误或者有看不懂的地方，多和喵博主交流。互相学习互相进步。如果这篇文章对你有帮助，可以给喵博主一个关注，你们的支持是我最大的动力。