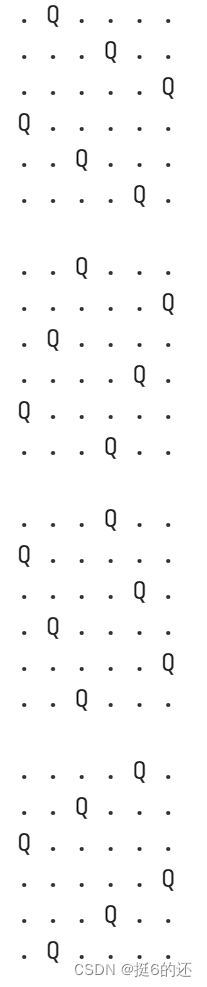
八皇后问题(*)

在国际象棋中，皇后是最厉害的棋子，可以横走、直走，还可以斜走。棋手马克斯·贝瑟尔 1848 年提出著名的八皇后问题：即在 8 × 8 的棋盘上摆放八个皇后，使其不能互相攻击 —— 即任意两个皇后都不能处于同一行、同一列或同一条斜线上。例如：

现在我们把棋盘扩展到?n×n?的棋盘上摆放?n?个皇后，请问该怎么摆？

请编写程序，输入正整数?n，输出全部摆法（棋盘格子空白处显示句点“.”，皇后处显示字母“Q”，每两个字符之间空一格）。

输入格式

正整数?n(n>0)

输出格式

若问题有解，则输出全部摆法（每两种摆法之间空一行）。
若问题无解，则输出 None。

要求：试探的顺序按从上到下逐行进行，其中每一行按从左到右的逐格进行，请参看输出样例2。

输入样例1

3

输出样例1

None

输入样例2

6

?

输出样例2

方法：回溯法。

思路：通过递归来控制层数，判断循环来控制判断当前层的的每一个位置的有效性，如果能放，则放，然后考虑放下一层，如果不能放，则继续考虑本层的下一个位置。

?递归的终止条件1为：所有层都已经放完了，那么此时就将这个棋盘（二维数组）存起来。

递归的终止条件2（同样是循环的终止条件）为：本层的所有位置都考虑完了。

那么这个问题可以分这几个子问题：

1.判断当前位置是否能放

2.存储棋盘（二维数组）

3.递归终止后回溯到根，要保证棋盘恢复到递归调用前的状态（递归放置的'Q'要清除才能不干扰下一次的递归）

速解：

1.定义一个函数IsValid，判断列，45度斜线，135度斜线。（不判断行是因为行只可能放一个）

2.用三维数组a[3000][n][n]，传参时函数参数写a[][n][n]，n维数组（n>=1）的第一个参数可以不写,因为数组的n-1维的数据尺寸已经确定。

3.回溯完后把原来放'Q'的位置恢复成放 '.' 。

至此，问题全部梳理出来了。

完整代码如下：

#include <stdio.h>
#include <stdlib.h>

//初始化棋盘
void clearboard(int sz, char(*board)[sz])
{
	for (int i = 0; i < sz; i++)
	{
		for (int j = 0; j < sz; j++)
		{
			board[i][j] = '.';
		}
	}
}
//判断当前位置的合法性
int IsValid(int sz, char(*board)[sz], int row, int col)
{
	//列判断
	for (int i = 0; i < sz; i++)
	{
		if (board[i][col] == 'Q')
			return 0;
	}
	//对角线判断
	for (int i = 0; i < sz; i++)
	{
		for (int j = 0; j < sz; j++)
		{
			if (j == i - row + col)
			{
				if (board[i][j] == 'Q')
					return 0;
			}
			if (row + col - i == j)
			{
				if (board[i][j] == 'Q')
					return 0;
			}
		}
	}
	return 1;
}
void memory(int sz, char a[][sz][sz], int* k, char(*board)[sz])
{
	for (int i = 0; i < sz; i++)
	{
		for (int j = 0; j < sz; j++)
		{
			a[(*k)][i][j] = board[i][j];
		}
	}
	(*k)++;
}
void Tracing(int sz, char a[][sz][sz], char(*board)[sz], int* k, int row)
{
	if (row == sz)
	{
		memory(sz, a, k, board);
		return;
	}
	else
	{
		for (int i = 0; i < sz; i++)
		{
			//先不放，先看当前位置是否会被影响，如果不会就放
			//直接放可能覆盖原来放好的'Q'
			if (IsValid(sz, board, row, i))
			{
				board[row][i] = 'Q';
				Tracing(sz, a, board, k, row + 1);
				board[row][i] = '.';
			}
		}
	}
}
int main()
{
	int n = 0;
	scanf("%d", &n);
	char a[3000][n][n];
	char board[n][n];
	clearboard(n, board);
	int k = 0;
	Tracing(n, a, board, &k, 0);
	if (k == 0)
	{
		printf("None\n");
		return 0;
	}
	for (int i = 0; i < k; i++)
	{
		for (int j = 0; j < n; j++)
		{
			for (int m = 0; m < n; m++)
			{
				printf("%c", a[i][j][m]);
				if (m < n - 1)
					printf(" ");
			}
			printf("\n");
		}
		if (i < k - 1)
			printf("\n");
	}
}