3 -灰度变换和空间滤波

本章目标：

1. 理解空间域处理（spatial domain processing）的意义，以及与变换域处理（transform domain processing）的区别
2. 熟悉灰度变换（intensity transformations）所用的主要技术
3. 理解图像直方图（image histograms）的物理意义，以及如何被用于图像增强（image enhancement）
4. 理解空间滤波（spatial filtering）的机制，以及如何形成
5. 理解解空间卷积和相关（spatial convolution and correlation）的主要原理
6. 熟悉空间滤波的主要类型，以及如何被运用
7. 理解空间滤波之间的关系，低通滤波的基本作用
8. 当单一图像增强方法（enhancement methods）失效的情况下，学习组合使用多种图像增强方法

一、背景

本章讨论的所有图像处理技术都基于空间域——对图像像直接操作

1.1 灰度变换和空间滤波基础

一些概念重申：

• 亮度： 图像的明暗程度，灰度值越大越亮，反之，越暗
• 对比度： 图像中最大灰度值与最小灰度值之间的差值
• 饱和度： 图像上的颜色种类个数有多少，越多该值越高，图片看上去很鲜艳，反之，图片看上去不自然
• 分辨率： 单位长度内包含的像素个数 ，越大，图片越清晰

---

$$g(x,y)=T[f(x,y)]$$
上述式子将贯穿本章，其中 ：

• $f(x,y)$是输入图片，$g(x,y)$是输出图片，$T$是一个关于像素点$(x,y)$邻域的运算算子
• 算子$T$可以作用于单张图片上的像素点（pixels of a single image），也可以作用于多张图片上的像素点（pixels of a set of images）

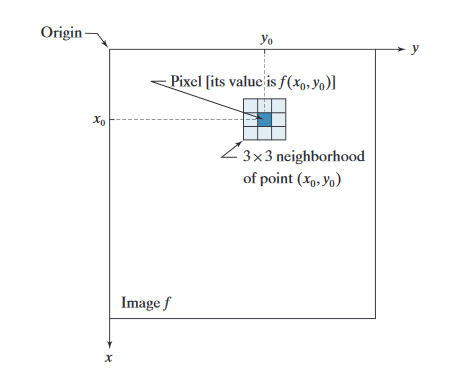
• 像素点$(x_0,y_0)$是一幅图像中的任意位置（arbitrary location）
• 上述坐标中，以该像素点为中心的 $3\times 3$ 正方形【一般是矩形 rectangular】就为该点的邻域（neighborhood）

---

最小的邻域为 $1\times 1$ , 此时$T$就为灰度（灰度级 gray-level 或映射 mapping）变换函数transformation function——结果仅取决于点的灰度（又称点处理技术point processing techniques，反之邻域处理技术neighborhood processing techniques） , 上述式子可以简化为
$$s=T(r)$$

此时，用 $s$ 和 $r$分别表示 $g$ 和 $f$在任意位置$(x,y)$的灰度值

---

灰度变换函数（intensity transformation） $T$小总结：

1. 直接对原图进行操作——空间域；是对单个像素点操作——点操作
2. 主要目的是进行图像增强
   • 改善图片质量，显示更多细节，提高图像对比度
   • 有选择的突出图像中感兴趣的特征，抑制不需要的特征
   • 有效改变图像的直方图分布，使像素的分布更均匀

二、一些基本的灰度变换函数

灰度变换函数类型：

• 线性变换 —— 连续和分段函数
• 非线性变换 —— 对数logarithmic和幂律函数 power-law

注： 一幅图像的灰度范围为 $[L_{min},L_{max}]$

2.1 线性灰度变换

2.1.1 连续函数

作用： 对图像的对比度和亮度进行调整
$$s=a\times r+b$$

$a$影响对比度，$b$影响亮度

?? 1. $a>1$ : 增强对比度
?? 2. $a<1$ : 降低对比度
?? 3. $b>0$ : 增加图像亮度
?? 4. $b<0$ : 降低图像亮度
?? 5. $a=?1,b=L_{max}$ : 图像翻转IMAGE NEGATIVES

2.1.2 分段函数

作用： 增强图像中感兴趣区域的灰度值，而抑制不感兴趣的灰度区域。通用公式如下：
$$s=?\begin{array}{l}\frac{s_1}{r_1}?r,r<r_1\\ \frac{s_2?s_1}{r_2?r_1}?(r?r_1),r_1\le r\le r_2\\ \frac{255?s_2}{255?r_2}?(r?r_2),r>r_2\end{array}$$

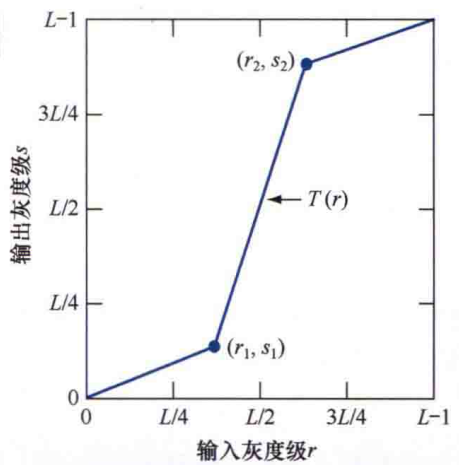
1. 对比拉伸函数 contrast stretching function
   作用： 将原图的灰度范围限制为自定义范围，增强感兴趣区域

r_min, r_max = 255, 0
for i in range(image.shape[0]):
    for j in range(image.shape[1]):
        for k in range(image.shape[2]):
            if image[i, j, k] > r_max:
                r_max = image[i, j, k]
            if image[i, j, k] < r_min:
                r_min = image[i, j, k]
r1, s1 = r_min, 0
r2, s2 = r_max, 255
k1 = s1/r1
k3 = (255-s2)/(255-r2)
k2 = (s2 - s1)/(r2 - r1)

precewise_img = np.zeros((image.shape[0], image.shape[1], 3), dtype=np.float32)
for i in range(image.shape[0]):
    for j in range(image.shape[1]):
        for k in range(image.shape[2]):
            if r1 <= image[i, j, k] <= r2:
                precewise_img[i, j, k] = k2*(image[i, j, k] - r1)
            elif image[i, j, k] < r1:
                precewise_img[i, j, k] = k1*image[i, j, k]
            elif image[i, j, k] > r2:
                precewise_img[i, j, k] = k3*(image[i, j, k] - r2)

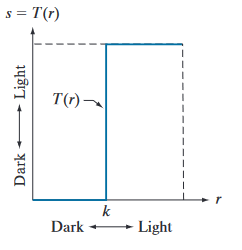
2. 阈值处理函数 thresholding function

当$r_1=r_2,s_1=0,s_2=L_{max}$时——上述的极限情况，此时分段线性函数便是阈值处理函数：$K$以下是黑色，以上是白色——产生一幅二级（值）图像a two level (binary) image

3. 灰度级分层 Intensity-Level Slicing
作用：
?? a) 可以将感兴趣取悦内的所有灰度值显示为一个值，而将其他区域的显示为另一个值——得到二值图像；
??b)可以将感兴趣区域变亮（或变暗），但保持图像中其他灰度值不变

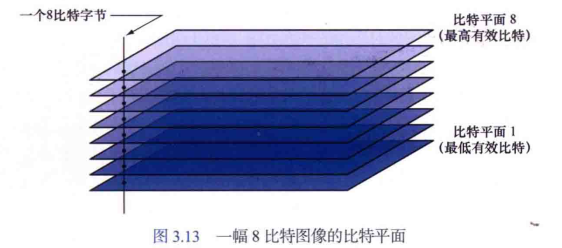
4. 比特平面分层 Bit-Plane Slicing

• 灰度值是由比特组成的整数，如在一幅256（0~255）级灰度图象中，一个灰度值由8比特（$2^8$）组成，此时可以称这幅图为8比特图
• $x$比特图像可由$x$个1比特平面组成，每个比特平面都是一个二值图像，比如8比特图像由8个1比特平面组成
• 最高有效的4个平面（尤其是其中较高的两个平面）包含大量具有视觉意义的数据

注：具体运算： https://blog.csdn.net/lxw234lxw/article/details/124022059

作用：
?? 1. 用来进行图像压缩 image compression
?? 2. 用来进行图像重建——存储4个最高有效比特平面，就能以可接受的细节和色调重建原图像【重建 reconstruction： 将第n个平面的像素乘以$2^{n?1}$，再将得到的所有平面相加】

2.2 非线性灰度变换

2.2.1 对数函数

作用： 压缩像素值的动态范围，将图像的低灰度值部分扩展，高灰度值部分压缩—— 对图像中低灰度值（暗）的细节进行增强

注： 反对数（指数）函数功能相反

$$s=clog(1+r)$$

	precewise_img = np.zeros((image.shape[0], image.shape[1], 3), dtype=np.float32)
    for i in range(img.shape[0]):
        for j in range(img.shape[1]):
        	for k in range(image.shape[2]):
            precewise_img[i][j][k] = math.log(1+img[i][j][k])
    # 归一化以及转回np.unit8
    cv2.normalize(precewise_img, precewise_img, 0, 255, cv2.NORM_MINMAX)
    img = cv2.convertScaleAbs(precewise_img)

2.2.2 幂律函数

作用：主要用于图像的校正，
??1. 可以对漂白的图片或过黑的图片进行修正，
??2. 可以增强对比度
$$s=c{r}^{\gamma },r\in [0,1]$$
考虑到偏移，也将上述式子写成如下形式：
$$s=c(r+?{)}^{\gamma }$$

三、图像直方图

• 令 $r_k$（k = 0,1,2,…,L-1）表示一幅 L 级灰度数字图像$f(x,y)$的灰度
• $M$ 和 $N$分别是图像的行数和列数

直方图 histogram： 关于图像灰度的函数，该函数的输出是图像中各个灰度级出现的次数或频率

• 非归一化直方图 unnormalized histogram ：
  $$h(r_k)=n_k,k=0,1,2,...,L?1$$
• 归一化直方图 normalized histogram ：
  $$p(r_k)=\frac{h(r_k)}{MN}=\frac{n_k}{MN}$$

• 一般使用归一化直方图，将此直方图简单地称为直方图或图像直方图 histograms or image histograms
• $p(r_k)$是对图像中出现的灰度级的概率的估计
• 直方图形状与图像外观相关

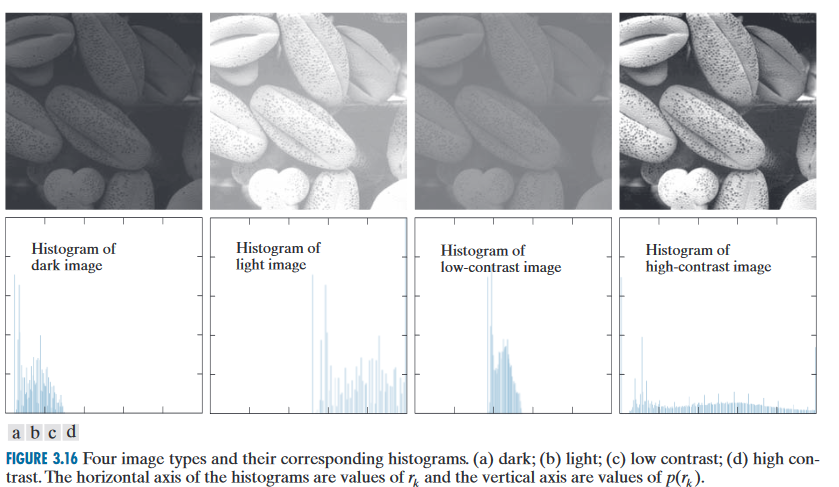
发现： 像素占据整个灰度级并且均匀分布的图像，将具有高对比度的外观和多种灰色调

3.1 直方图均衡化

直方图均衡化： 把原始图像的灰度直方图从比较集中的某个灰度区间 映射到 更广泛的灰度范围内的分布，且各灰度级的频次较为均衡——这样一幅图像中的各个位置都能看到，提高对比度

方法：

1. 假设图像的初始灰度级是连续的，令 $r$ 表示归一化的原图像，$s$为修正后的图像，有$0?r,s?1$，其中，0 表示为黑色，1 表示为白色
2. 对 $r$ 进行变换 ： $s=T(r)$，满足：
   • $T(r)$ 在区间 $0?r?1$ 内单调递增
   • 在区间 $0?r?1$ 内，有 $0?T(r)?1$
   • 反变换同样满足上述两个条件

注：

• 第一个条件保证输出的灰度值从不小于对应的输入值——防止因灰度反转而产生伪像
• 第二个条件保证输出的范围同输入的范围相同
• 此外，如果将第一个条件改为严格单调递增,保证反变换的映射是一对一的

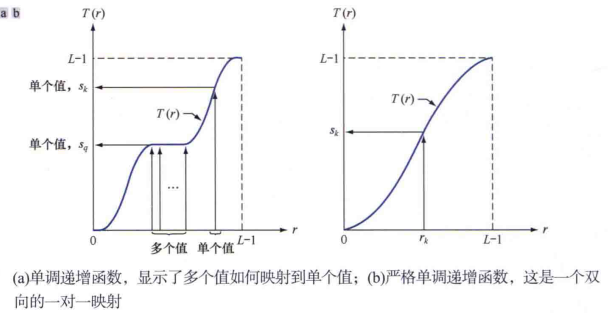
令 $p_r(r)$ 和 $p_s(s)$表示原图和修改后图中灰度级的概率密度函数；概率论基本结论，已知 $p_r(r)$和$T(r)$，且$T(r)$连续可微，则$p_s(s)$可由$p_r(r)$和$T(r)$表示。推导如下：

---

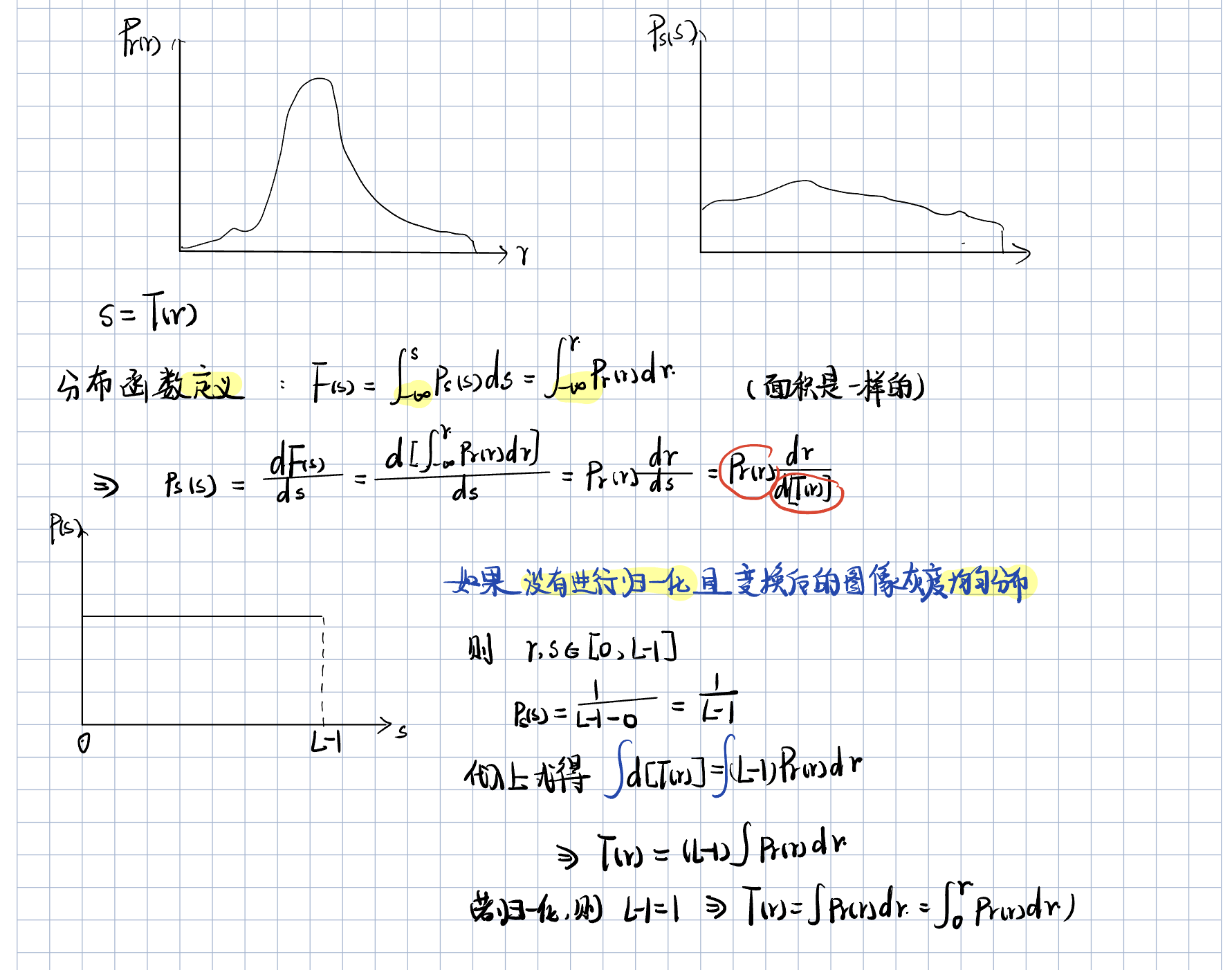
若图像的灰度值是离散的，则使用概率求和代替概率密度函数与积分：
$$p_r(r_k)=\frac{n_k}{MN}$$
$$s_k=T(r_k)=(L?1)\sum _{j=0}^k{p}_r(r_j),k=0,1,2,...,L?1$$

3.2 直方图匹配（规定化）

背景： 直方图均衡化可以根据输入图像的灰度级的概率密度函数自动 生成一个变换函数，继而得到一个直方图均匀分布的图像。但有时候，需要图像具有一特定的直方图形状
直方图匹配（规定化）： 将原图像的直方图变换为指定的形式，而不只是均匀分布的直方图

方法：

1. 假设图像的初始灰度级是连续的，令$p_r(r)$ 和 $p_z(z)$ 分别为原始图像的灰度级概率密度、规定化后的概率密度
2. 对原始图像进行直方图均衡化： $s=T(r)=(L?1){\int }_0^r{p}_r(w)dw$
3. 对规定化的图像进行直方图均衡化：$G(z)=T(r)=(L?1){\int }_0^z{p}_z(v)dv$
4. 有$s=G(z)=T(r)$，则$z=G^{?1}(s)=G^{?1}(T(r))$，得到了原始图像像素到规定化后图像像素的一个应黑色

---

离散形式：
使用原始图像的像素
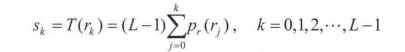使用目标-规定化后的图像的像素

3.3 局部直方图处理

方法： 定义一个邻域，并将其中心在水平方向或垂直方向上从一个像素移动到另一个像素。在每个位置，计算该邻域的直方图，使用直方图均衡化或规定化

四、空间滤波

滤波： 修改或抑制图像的规定频率分量
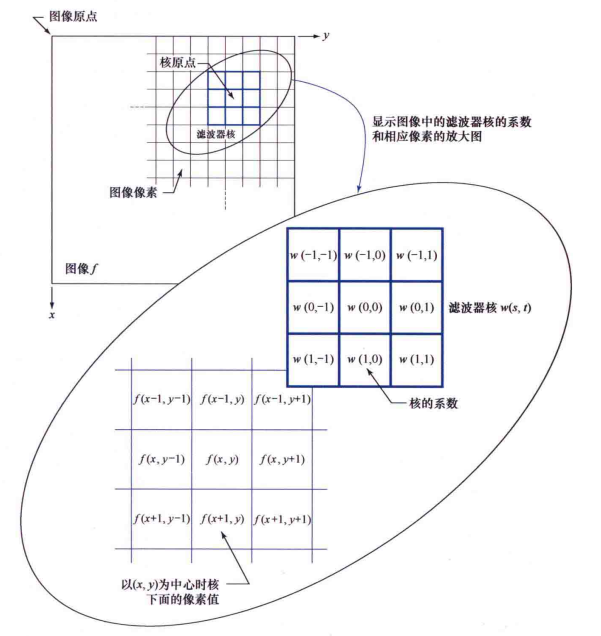
空间滤波： 通过把每个像素的值替换为该像素及其邻域的函数值来修改图像

4.1 线性空间滤波原理

前提： 图像$f$和滤波器核$w$

滤波器核$w$是一个阵列，大小定义了运算的邻域大小，系数决定该滤波器的性质

一般公式： 设核大小为 $m\times n$，$m=2a+1，n=2b+1$，a和b为非负整数——此为奇数大小的核
$$g(x,y)=\sum _{s=?a}^a\sum _{t=?b}^{b}w(s,t)f(x+s,y+t)$$

4.2 空间相关与卷积

相关（Correlation）： 在图像上移动核的中心，并且在每个位置计算乘积之和

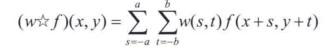
卷积（Convolution）： 把相关运算的核旋转180度

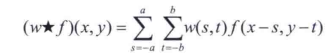
注：

• 当核的值关于其中心对称时，两者结果相同
  

4.3 可分离滤波器核

二维函数的可分离： 一个二维函数可以写为两个一维函数的乘积，$G(x,y)=G_1(x)G_2(y)$
可分离核： 一个核为一个矩阵，可分离意味着该举证可以表示为两个向量的外积，$w=c{r}^T$

---

如果一个核，可以分解为两个更简单的核，且满足$w=w_1★w_2$,则该可分离核与一幅图像的卷积，等于先跟$w_1$卷积，再跟$w_2$卷积

---

大小为$M\times N$的图像与大小为$m\times n$的核进行卷积需要进行MNmn次乘法和加法运算，而是用可分离核则只需要MN(m+n)次乘法核加法计算——第一次MNm,第二次MNn

---

如何证明一个核是可分离的： 该矩阵的秩为1

4.4 空间域滤波与频率域滤波

背景：

• 空间域与频率域之间的联系是傅里叶变换
• 满足一些温和条件的函数（如图像）可以表示为不同频率核振幅的正弦波之和
• 图像的外观依赖于正弦分量的频率

空间域转换到频率域中，进行低通滤波，再返回空间与

五、平滑（低通）空间滤波器

作用： 将第灰度的急剧过渡——降噪、减少图像中的无关细节、平滑因灰度级数量不足导致的图像中的伪轮廓——奶油抹匀了

1. 盒式滤波器：核系数相同（通常为1）——可分离
2. 低通高斯滤波器：可分离
   
   

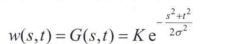
六、锐化（高通）空间滤波器

作用： 突出灰度中的过渡
类型： 一般可以分为基于一阶导数和二阶导数类型

6.1 基础

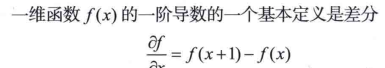
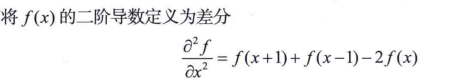
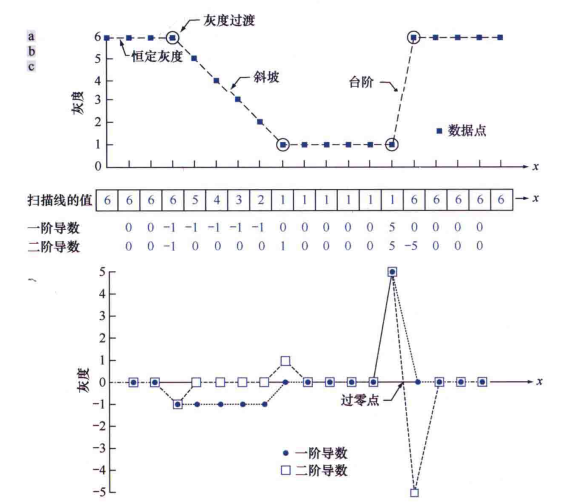
6.1 基于一阶导数的锐化滤波器——梯度

6.2 基于二阶导数的锐化滤波器——拉普拉斯