滑动窗口第二弹

力扣1658.将x减到0点最小操作数?

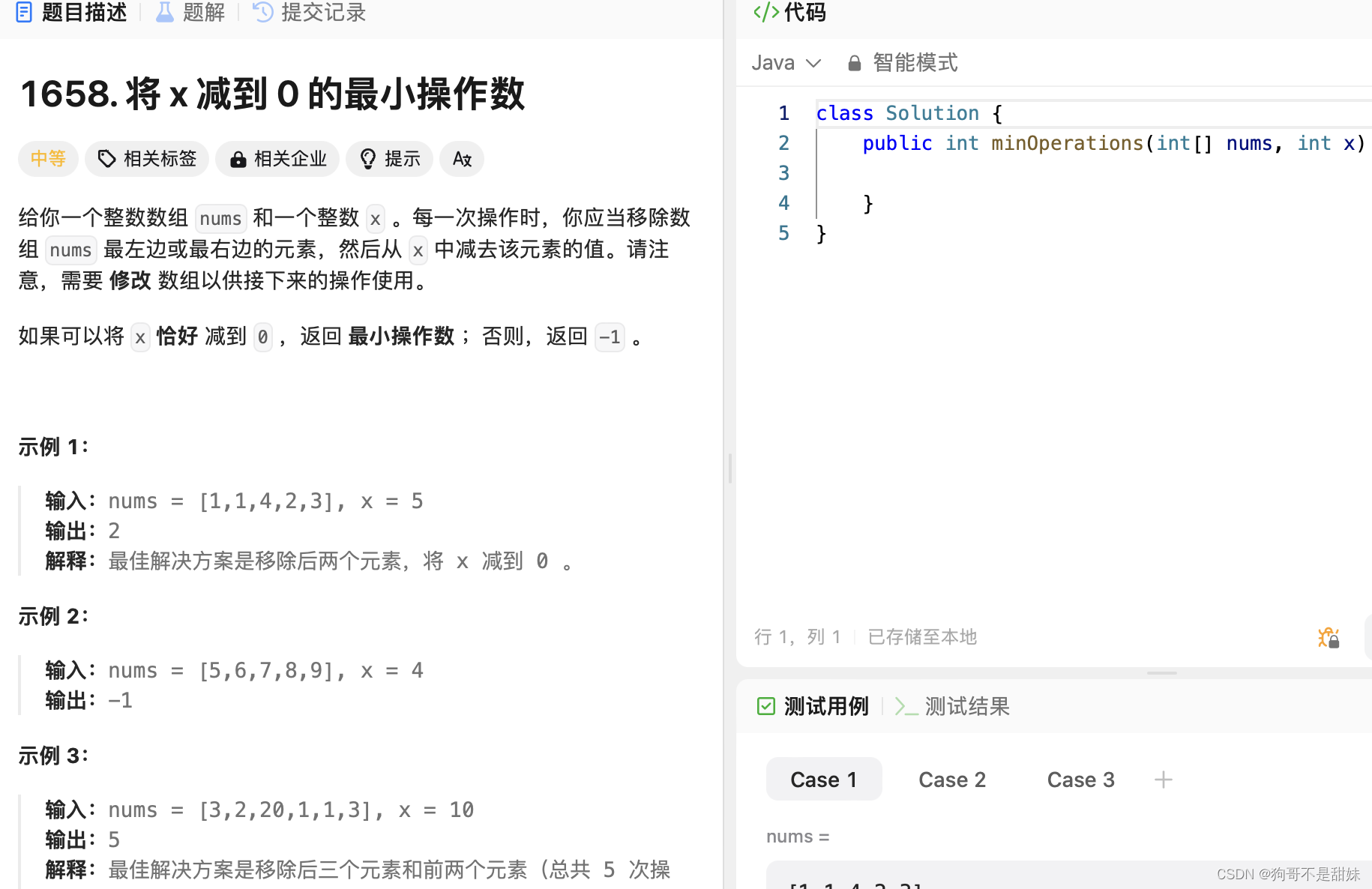
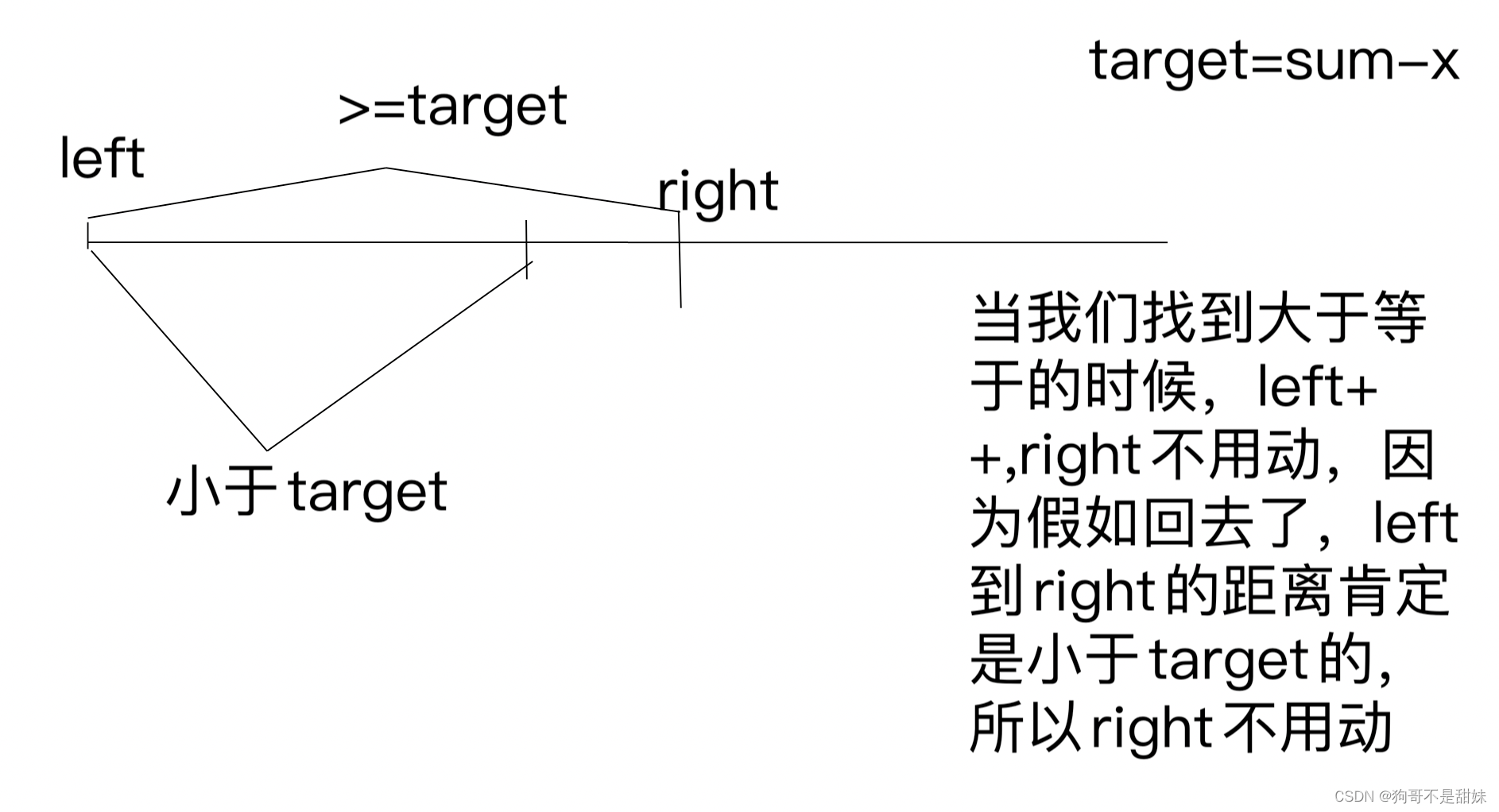
正难则反

想法永远是从暴力开始，然后观察能否使用滑动窗口优化

最后总长度-一个中间区域的最长

解法:滑动窗口

left=0,right=0

进窗口

判断

出窗口

更新结果

??里面的值必须都是正的才能使用滑动窗口

class Solution {
    public int minOperations(int[] nums, int x) {
    int left=0;
    int right=0;
    int n=nums.length;
    int sum=0;
    for(int a:nums)sum+=a;
    int target=sum-x;
    int tmp=0;
    int len=-1;
    if(target<0)return-1;
//我认为当前比较难的代码编写，就是很可能理解不出来两个循环的条件哪个在里面哪个在外面
//出窗口的在里面，入窗口的在外面
    while(right<n){      
    tmp+=nums[right];        //进窗口   
        while(tmp>target){   //出窗口的条件
         tmp-=nums[left];
              left++;
        }
         if(tmp==target){
            len=Math.max(len,right-left+1);
        }
           right++;
    }
    if(len==-1) return len;
    else return n-len;
    }
}

力扣904.水果成篮

最后翻译题意，就是找最长的子数组，在这段子数组中最多有两种类型不同

法1:暴力解法+哈希表

法2:滑动窗口（判断right是否要回去)

解法1:模拟哈希表

class Solution {
    public int totalFruit(int[] fruits) {
     int left=0;
     int right=0;
     int count=0;
     //我们常常借助哈希表来去统计有没有重复的次数
     int len=0;
     int n=fruits.length;
     //如果是字符集，可以使用这个来模拟,下标表示种类，数字表示个数
      //模拟哈希表，因为他的长度在那里，为什么是n+1,因为可以不用去修改东西，0的下标就是1而不是0，因为最少也是一种。这样就可以使，假如fruit[right]==1，那么对应的t[1]，而且不用考虑太多，n+1是肯定够的

     int []t=new int[n+1];
     //统计窗口内水果的种类
     // Map<Integer,Integer>hash=new HashMap<Integer,Integer>();
         while(right<n){
    //看你模拟的哈希表中，是否是0，假如是0就说明没有出现这个种类，那么种类就需要++
             //count
        if(t[fruits[right]]==0){
         count++;}
         t[fruits[right]]++;
         
       //出窗口
         while(count>2){
             t[fruits[left]]--;
             if(t[fruits[left]]==0){
                 count--;
             }
               left++;
         }
         //len，注意什么时候更新结果，是等于2的时候更新结果，假如放到前面，那么就变成等于三也去更新结果了。
         len=Math.max(len,right-left+1);
         right++;
     }
     return len;
    }
}

使用HashMap

class Solution {
    public int totalFruit(int[] fruits) {
     int left=0;
     int right=0;
     int count=0;
     //我们常常借助哈希表来去统计有没有重复的次数
     int len=0;
     int n=fruits.length;
     //如果是字符集，可以使用这个来模拟,下标表示种类，数字表示个数
   //  int []t=new int[n+1];
     //统计窗口内水果的种类
     Map<Integer,Integer>hash=new HashMap<Integer,Integer>();
         while(right<n){
    //看你模拟的哈希表中，是否是0，假如是0就说明没有出现这个种类，那么种类就需要++
             //count
         hash.put(fruits[right],hash.getOrDefault(fruits[right],0)+1);
         //包含的代码不会写
         while(hash.size()>2){
             //put也是改变的意思，不能光认为它是增加的含义
          hash.put(fruits[left],hash.get(fruits[left])-1);
          if(hash.get(fruits[left])==0){
              hash.remove(fruits[left]);
          }
          left++;
         }
         //len
         len=Math.max(len,right-left+1);
         right++;
     }
     return len;
    }
}

力扣438.找到字符串中所有字母异位词(两种方法)

//如何判断两个字符是不是异位词

滑动窗口

两类题：

right不断变化，left常常不变，窗口的大小不固定

但是这个滑动窗口是固定的

法一：

补充知识点:字符串的charAt(i) 获取字符串

s.charAt(i),返回字符串第i个下标的值，

Arrays.equals(x1,x2);

class Solution {

    public static List<Integer> findAnagrams(String s, String p) {
        int left = 0;
        List<Integer> res = new ArrayList<>();
        int m = p.length();
        int right = 0;
        int[] sCnt = new int[26];
        int[] pCnt = new int[26];
        for (int i = 0; i < p.length(); i++) {
//这个就是把p的字符，按照acil下标码顺序减去a存入（模拟的）哈希表里面。
            pCnt[p.charAt(i) - 'a']++;
        }
        while (right <s.length()) {
//这个就是把s的字符，按照acil下标码顺序减去a存入（模拟的）哈希表里面。
            sCnt[s.charAt(right)-'a']++;
            if (right - left + 1 > m) {
                sCnt[s.charAt(left)-'a']--;
                left++;
            }
//看两个数组是否相同，
            if(right-left+1==m&&Arrays.equals(sCnt,pCnt)){
                res.add(left);
            }
            right++;
        }
        return  res;
    }
}

法二：

他是通过count 来判断符不符合条件

他的想法：

开始和法1相同，都是模拟哈希，然后把要去重的存起来，然后把遍历s

//这个的意思是，pCnt是我们要的，那么sCnt就是要看它里面有没有和pCnt一样的，而且一个要点，他的字符串可以任意顺序，所以我们假如sCnt咩有pCnt里面那个东西，那么count不更改，假如有，但是大于他，就说明多了，count也不会++，就像是一个蛋糕，他先给你准备壳，你照着壳来做蛋糕

if(sCnt[s.charAt(right)-'a']<=pCnt[s.charAt(right)-'a'])
? ? ? ? ? ? ? ? count++;

第二块

? ?if(sCnt[s.charAt(left)-'a']<=pCnt[s.charAt(left)-'a']){
? ? ? ? ? ? ? ? ? ? count--;}

这个是说假如你去除的是一个必要的，那么就说明这一段不是，但是count会减一次，他就像是统计必要的这三个字母，你假如少了一个，那么count就--

 public static List<Integer> findAnagrams(String s, String p) {
        int left = 0;
        List<Integer> res = new ArrayList<>();
        int m = p.length();
        int right = 0;
        int[] sCnt = new int[26];
        int[] pCnt = new int[26];
        int count=0;
        for (int i = 0; i < p.length(); i++) {
            pCnt[p.charAt(i) - 'a']++;
        }
        while (right <s.length()) {
            sCnt[s.charAt(right)-'a']++;
            if(sCnt[s.charAt(right)-'a']<=pCnt[s.charAt(right)-'a'])
                count++;
            if (right - left + 1 > m) {

                if(sCnt[s.charAt(left)-'a']<=pCnt[s.charAt(left)-'a']){
                    count--;}
                sCnt[s.charAt(left)-'a']--;
                left++;
            }
            if(count==m){
                res.add(left);
            }
            right++;
        }
        return  res;
    }