【Math】重要性采样 Importance sample推导【附带Python实现】
【Math】重要性采样 Importance sample推导【附带Python实现】
文章目录
笔者在学习强化学习的过程中,经常遇到重要性采样的问题,这里简要记录一下推导过程方便以后查看。
1. Why need importance sample?
为什么需要重要性采样呢?假设我们目前有一个随机变量 X ~ X X\sim \mathcal{X} X~X, 并且该随机变量服从概率分布 p 0 ( X ) p_0(X) p0?(X),我们的目标是计算该随机变量的期望 E X ~ p 0 [ X ] \mathbb{E}_{X\sim p_0}[X] EX~p0??[X],我们同样知道随机变量 X X X 的另一个易于获得的概率分布 p 1 ( X ) p_1(X) p1?(X),我们如何通过这个易于获得的概率分布来计算在概率分布 p 0 ( X ) p_0(X) p0?(X)下的期望 E X ~ p 0 [ X ] \mathbb{E}_{X\sim p_0}[X] EX~p0??[X]呢?这个技巧就被称作重要性采样(Importance Sample)。
2. Derivation of Discrete Distribution
假设随机变量 X X X是服从离散的概率分布,并且我们在概率分布 p 1 ( X ) p_1(X) p1?(X)下,有一致同分布的采样 { x i } i = 1 n \{x_i\}^n_{i=1} {xi?}i=1n?。在概率分布 p 0 ( X ) p_0(X) p0?(X)下的期望 E X ~ p 0 [ X ] \mathbb{E}_{X\sim p_0}[X] EX~p0??[X]就可以用下式来进行表示
E X ~ p 0 [ X ] = ∑ x ∈ X p 0 ( x ) x = ∑ x ∈ X p 1 ( x ) p 0 ( x ) p 1 ( x ) x ? f ( x ) = E X ~ p 1 [ f ( X ) ] E X ~ p 0 [ X ] = E X ~ p 1 [ f ( X ) ] ≈ f ˉ = 1 n ∑ i = 1 n f ( x i ) = 1 n ∑ i = 1 n p 0 ( x i ) p 1 ( x i ) ? importance?weight x i \mathbb{E}_{X\sim p_0}[X] = \sum_{x\in\mathcal{X}}p_0(x)x = \sum_{x\in\mathcal{X}}p_1(x)\underbrace{\frac{p_0(x)}{p_1(x)}x}_{f(x)} = \mathbb{E}_{X\sim p_1}[f(X)] \\ \mathbb{E}_{X\sim p_0}[X] = \mathbb{E}_{X\sim p_1}[f(X)] \approx \bar{f} = \frac{1}{n} \sum^n_{i=1}f(x_i) = \frac{1}{n} \sum^n_{i=1} \underbrace{\frac{p_0(x_i)}{p_1(x_i)}}_{\text{importance weight}}x_i EX~p0??[X]=x∈X∑?p0?(x)x=x∈X∑?p1?(x)f(x) p1?(x)p0?(x)?x??=EX~p1??[f(X)]EX~p0??[X]=EX~p1??[f(X)]≈fˉ?=n1?i=1∑n?f(xi?)=n1?i=1∑n?importance?weight p1?(xi?)p0?(xi?)???xi?
其中, p 0 ( x i ) p 1 ( x i ) \frac{p_0(x_i)}{p_1(x_i)} p1?(xi?)p0?(xi?)?被称为重要性权重,那么通过这个重要性权重,我们就可以在概率分布 p 1 ( X ) p_1(X) p1?(X)下进行采样 { x i } i = 1 n \{x_i\}^n_{i=1} {xi?}i=1n?,来计算期望 E X ~ p 0 [ X ] \mathbb{E}_{X\sim p_0}[X] EX~p0??[X]了。
3. Derivation of Continuous Distribution
类似地,假设随机变量 X X X是服从连续的概率分布,并且我们在概率密度函数 p 1 ( x ) p_1(x) p1?(x)下,有一致同分布的采样 { x i } i = 1 n \{x_i\}^n_{i=1} {xi?}i=1n?。在概率函数 p 0 ( x ) p_0(x) p0?(x)下的期望 E X ~ p 0 [ X ] \mathbb{E}_{X\sim p_0}[X] EX~p0??[X]就可以用下式来进行表示
E
X
~
p
0
[
X
]
=
∫
?
∞
∞
x
×
p
0
(
x
)
d
x
=
∫
?
∞
∞
p
1
(
x
)
×
p
0
(
x
)
p
1
(
x
)
×
x
?
f
(
x
)
d
x
=
E
X
~
p
1
[
f
(
X
)
]
\mathbb{E}_{X\sim p_0}[X] = \int_{-\infty}^\infty x \times p_0(x) dx = \int_{-\infty}^\infty p_1(x) \times \underbrace{\frac{p_0(x)}{p_1(x)}\times x}_{f(x)} dx = \mathbb{E}_{X\sim p_1}[f(X)] \\
EX~p0??[X]=∫?∞∞?x×p0?(x)dx=∫?∞∞?p1?(x)×f(x)
p1?(x)p0?(x)?×x??dx=EX~p1??[f(X)]
然后我们使用大量的离散采样来估计连续的期望
E
X
~
p
0
[
X
]
=
E
X
~
p
1
[
f
(
X
)
]
≈
f
ˉ
=
1
n
∑
i
=
1
n
f
(
x
i
)
=
1
n
∑
i
=
1
n
p
0
(
x
i
)
p
1
(
x
i
)
?
importance?weight
x
i
\mathbb{E}_{X\sim p_0}[X] = \mathbb{E}_{X\sim p_1}[f(X)] \approx \bar{f} = \frac{1}{n} \sum^n_{i=1}f(x_i) = \frac{1}{n} \sum^n_{i=1} \underbrace{\frac{p_0(x_i)}{p_1(x_i)}}_{\text{importance weight}}x_i
EX~p0??[X]=EX~p1??[f(X)]≈fˉ?=n1?i=1∑n?f(xi?)=n1?i=1∑n?importance?weight
p1?(xi?)p0?(xi?)???xi?
3. An Example
假设 X ∈ X = + 1 , ? 1 X\in\mathcal{X}={+1,-1} X∈X=+1,?1,概率分布 p 0 ( X ) p_0(X) p0?(X)满足
p 0 ( X = + 1 ) = 0.5 , p 0 ( X = ? 1 ) = 0.5 p_0(X=+1)=0.5, p_0(X=-1)=0.5 p0?(X=+1)=0.5,p0?(X=?1)=0.5
那么在概率分布 p 0 p_0 p0?下的期望即为:
E X ~ p 0 [ X ] = ( + 1 ) × 0.5 + ( ? 1 ) × 0.5 = 0 \mathbb{E}_{X\sim p_0}[X] = (+1)\times 0.5 + (-1) \times 0.5 = 0 EX~p0??[X]=(+1)×0.5+(?1)×0.5=0
假设另一个概率分布 p 1 ( X ) p_1(X) p1?(X)满足
p 0 ( X = + 1 ) = 0.8 , p 0 ( X = ? 1 ) = 0.2 p_0(X=+1)=0.8, p_0(X=-1)=0.2 p0?(X=+1)=0.8,p0?(X=?1)=0.2
那么在概率分布 p 1 p_1 p1?下的期望即为:
E X ~ p 1 [ X ] = ( + 1 ) × 0.8 + ( ? 1 ) × 0.2 = 0.6 \mathbb{E}_{X\sim p_1}[X] = (+1)\times 0.8 + (-1) \times 0.2 = 0.6 EX~p1??[X]=(+1)×0.8+(?1)×0.2=0.6
通过重要性采样,我们便可以通过在概率分布 p 1 ( X ) p_1(X) p1?(X)下的采样来计算在概率分布 p 0 ( X ) p_0(X) p0?(X)下的期望值,即
E X ~ p 0 [ X ] = 1 n ∑ i = 1 n p 0 ( x i ) p 1 ( x i ) x i \mathbb{E}_{X\sim p_0}[X] = \frac{1}{n}\sum_{i=1}^n \frac{p_0(x_i)}{p_1(x_i)}x_i EX~p0??[X]=n1?i=1∑n?p1?(xi?)p0?(xi?)?xi?
实现代码如下:
import numpy as np
import matplotlib.pyplot as plt
# reproducible
np.random.seed(0)
# 定义元素和对应的概率
elements = [1, -1]
probs1 = [0.5, 0.5]
probs2 = [0.8, 0.2]
# 重要性采样 importance sample
sample_times = 300
sample_list = []
i_sample_list = []
average_list = []
importance_list = []
for i in range(sample_times):
sample = np.random.choice(elements, p=probs2)
sample_list.append(sample)
average_list.append(np.mean(sample_list))
if sample == elements[0]:
i_sample_list.append(probs1[0] / probs2[0] * sample)
elif sample == elements[1]:
i_sample_list.append(probs1[1] / probs2[1] * sample)
importance_list.append(np.mean(i_sample_list))
plt.plot(range(len(sample_list)), sample_list, 'o', markerfacecolor='none', label='sample data')
plt.plot(range(len(average_list)), average_list, 'b--', label='average')
plt.plot(range(len(importance_list)), importance_list, 'g--', label='importance sampling')
plt.axhline(y=0.6, color='r', linestyle='--')
plt.axhline(y=0, color='r', linestyle='--')
plt.ylim(-1.5, 2.5) # 限制y轴显示范围
plt.xlim(0,sample_times) # 限制x轴显示范围
plt.legend(loc='upper right')
plt.show()
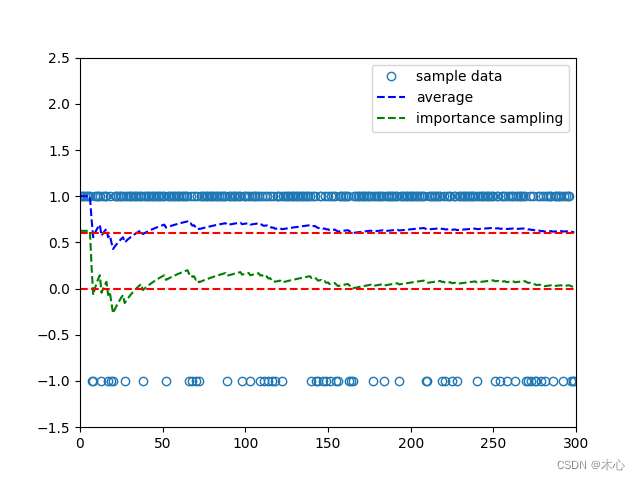
结果如下,可以看出之间用 p 1 ( X ) p_1(X) p1?(X)来进行期望的计算,随着样本数的增多,期望 E X ~ p 1 [ X ] \mathbb{E}_{X\sim p_1}[X] EX~p1??[X]越来越逼近0.6,但是经过重要性采样,结果越来越逼近0,符合期望 E X ~ p 0 [ X ] = 0 \mathbb{E}_{X\sim p_0}[X]=0 EX~p0??[X]=0。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!