代码随想录27期|Python|Day22|二叉树|235. 二叉搜索树的最近公共祖先|701.二叉搜索树中的插入操作|450.删除二叉搜索树中的节点
发布时间:2023年12月22日
235.?二叉搜索树的最近公共祖先
本题题干给出是BST,所以需要好好利用这个性质。
首先,如果一个节点是共同祖先,那么首先要满足值在[p, q]内,才能成为根节点。
但是,满足这个情况的节点可能有很多,但是最近的只有一个。比如下图:
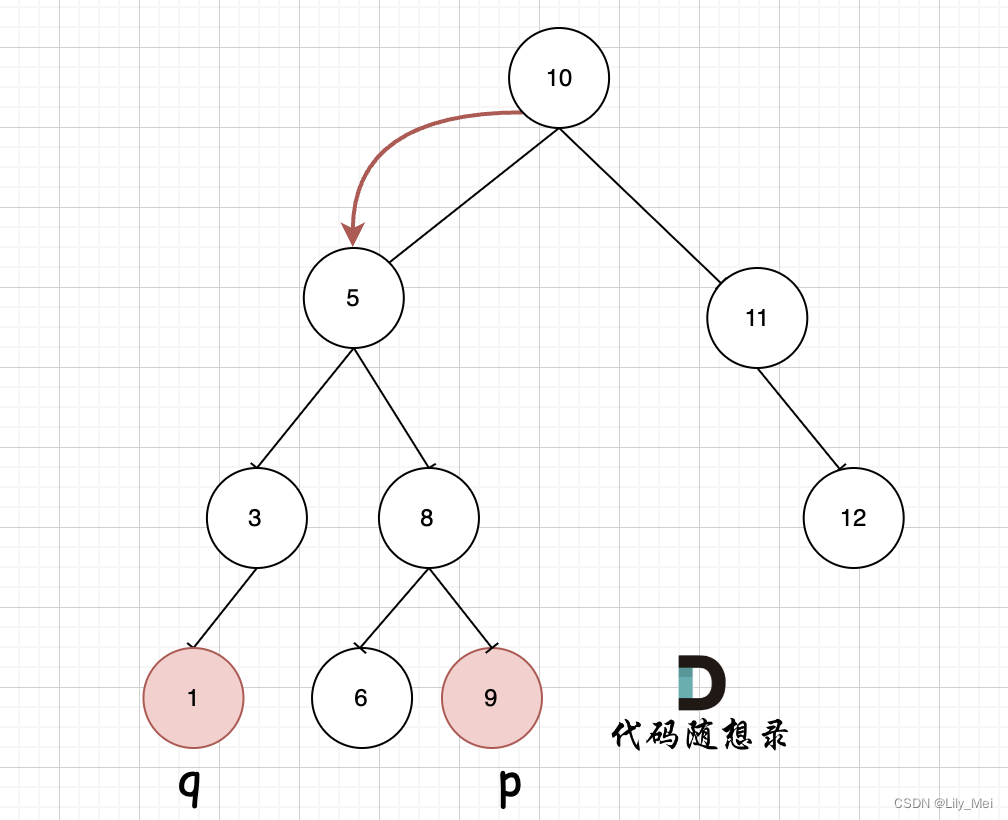
通过观察可以发现,如果从最顶端开始遍历,那么第一个落在[p, q]区间内的节点就是我们要找的共同祖先。?
递归
返回值的确定:由于是找到一个就返回,不需要联合left和right的逻辑,所以返回值为当前节点。
顺序:自上而下,大于p、q进左子树;小于p、q进右子树。
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution(object):
def lowestCommonAncestor(self, root, p, q):
"""
:type root: TreeNode
:type p: TreeNode
:type q: TreeNode
:rtype: TreeNode
"""
return self.traversal(root, p, q)
def traversal(self, node, p, q):
# 确定终止条件
if not node:
return node
# 如果当前节点大于p和q:去左子树
if node.val > p.val and node.val > q.val:
left = self.traversal(node.left, p, q)
if left is not None: # 如果左子树找到了区间内的第一个点,返回
return left
# 如果当前节点小于p和q:去右子树
elif node.val < p.val and node.val < q.val:
right = self.traversal(node.right, p, q)
if right is not None: # 找到区间内的第一个点,返回
return right
return node # 找到一个就返回,不需要遍历整个树,return需要返回值迭代
迭代更适合BST的遍历搜索。遍历顺序和递归是一致的。
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution(object):
def lowestCommonAncestor(self, root, p, q):
"""
:type root: TreeNode
:type p: TreeNode
:type q: TreeNode
:rtype: TreeNode
"""
# 迭代
while root:
if root.val > p.val and root.val > q.val:
root = root.left
elif root.val < p.val and root.val < q.val:
root = root.right
else:
return root
return None701.?二叉搜索树中的插入操作?
BST的一个性质:插入值都可以落在叶子节点(不重复的情况下)
利用上面这个性质,就变得十分甚至九分的简单:小于root进左子树;大于root进右子树。遇到空节点,创建新node。
插入的一个好处是不会改变已有的结构,只需要开花结果即可。?
递归
本题也是属于找到(构造)好就直接回溯返回根节点的,所以返回值是node,中间处理的时候需要left和right分别接住左右子树的返回值。
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution(object):
def insertIntoBST(self, root, val):
"""
:type root: TreeNode
:type val: int
:rtype: TreeNode
"""
node = root
if node is None:
node = TreeNode(val)
return node
# 中间处理:小于当前节点,进左子树
if node.val > val:
node.left = self.insertIntoBST(node.left, val)
# 大于当前节点,进右子树
elif node.val < val:
node.right = self.insertIntoBST(node.right, val)
return node # 找到(构造)一个满足条件的即返回,所以返回值是node迭代
迭代可以参考上一片BST的迭代写法。这样写的好处是可以直接按照顺序从上往下遍历。
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution(object):
def insertIntoBST(self, root, val):
"""
:type root: TreeNode
:type val: int
:rtype: TreeNode
"""
# 迭代
if root is None:
root = TreeNode(val)
return root
cur = root
# while 结束的时候cur停在和val并列的一层
while cur:
pre = cur
if cur.val > val:
cur = cur.left
else:
cur = cur.right
node = TreeNode(val)
# 需要用上一层的节点来指向val节点
if node.val < pre.val:
pre.left = node
else:
pre.right = node
return root450.?删除二叉搜索树中的节点?
和上面的添加节点只用在叶子节点添加不同,这里我们需要改变树的内部结构,类似链表的删除(虽然二叉树默认是链表形式储存的)。
| 没有该节点 | 返回None |
| 是叶子节点(左右都是空节点) | 直接删除 |
| 是中间节点,左空右不空 | 删除+衔接 |
| 是中间节点,左不空右空 | 删除+衔接 |
| 是中间节点,左右都不空 | 右子树继承+嫁接左子树 |
那么对应上面的每一种情况我们就可以确定递归函数的终止条件。
最后一种的删除方式可以参考下图:
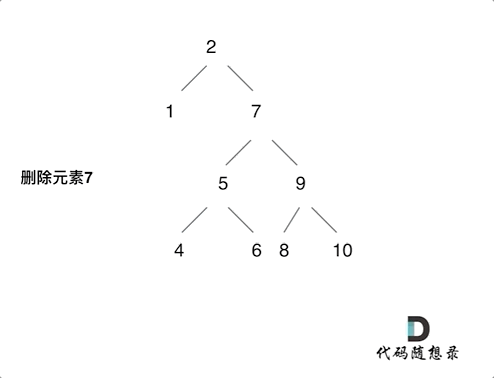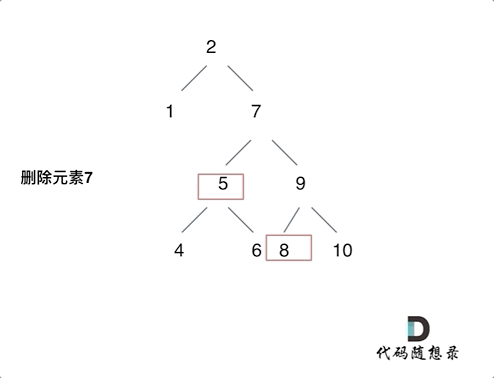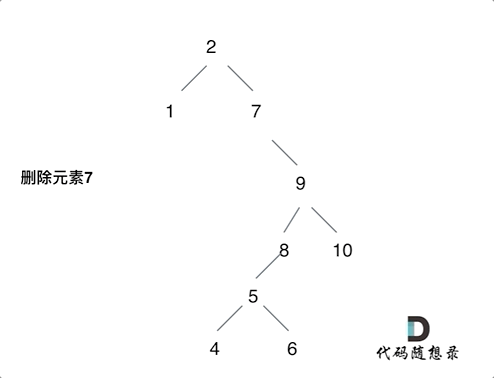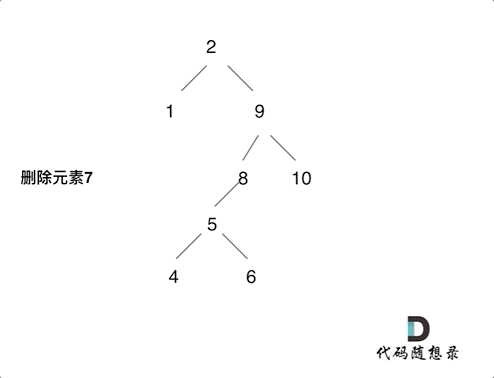
这里使用比较一般的递归解法,逐步实现每一种情况的分解。
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution(object):
def deleteNode(self, root, key):
"""
:type root: TreeNode
:type key: int
:rtype: TreeNode
"""
# <1> 没找到节点
if not root:
return None
if root.val == key:
# <2> 找到的是叶子节点
if root.left == None and root.right == None:
return None
# <3> 中间节点没有左子树
elif root.left == None:
return root.right
# <4> 中间节点没有右子树
elif root.right == None:
return root.left
# <5> 中间节点左右子树都有
else:
cur = root.right # 从右子树开始
# 找到比左子树根节点大的第一个数,也就是右子树的最左端
while cur.left:
cur = cur.left
# 原左子树嫁接到原右子树的最左端
cur.left = root.left
# 右子树继承原根节点
return root.right
# 递归
if root.val > key: # 小于走左子树
root.left = self.deleteNode(root.left, key)
elif root.val < key: # 大于走右子树
root.right = self.deleteNode(root.right, key)
return root?第22天完成🎉
文章来源:https://blog.csdn.net/m0_57527624/article/details/135147731
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- JavaScript DOM表单相关操作之表单验证
- vue-cli创建项目,vue项目目录介绍
- Tomcat Notes: Web Security
- 若依generator模块解读,Java小白入门(七)
- 优雅地使用python读取excel
- NumPy 中级教程——通用函数(ufuncs)
- POI:对Excel的基本写操作 整理1
- 非线性方程求根
- IOS-高德地图隐私合规示例-Swift
- 模型Model:QAbstractItemModel