4. 寻找两个正序数组的中位数

引流：人工智能领域专栏?

题目：

力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

给定两个大小分别为?m?和?n?的正序（从小到大）数组?nums1?和?nums2。请你找出并返回这两个正序数组的?中位数?。

算法的时间复杂度应该为?O(log (m+n))?。

【解题思路 】

从题目中，我们可以凝练出以下几个直接决定题目能解出来的点：

（1）两个数组的中位数，意味着把两个数组合并起来后取中间的那个数或者中间两个数的平均数；

（2）数组的长度有奇有偶，所以中位数是取中间那个数还是中间两个数的平均数，要分两种情况考虑；

（3）两个数组已经是升序排列，所以正常我们只需要把两个数组按照双指针的方法合并成一个升序数组即可，这个时间复杂度已经挺低了，为，然而题目要求时间复杂度为，意味着我们不能直接将两个数组合并后再找中位数；

（4）时间复杂度是二分法的时间复杂度，二分法的核心思想是：要在有序数组中查找第k大的数，可以每次都先排除数组中不包含第k个数的一半数；

????????综合上述分析，本题实际上就是要从两个有序数组中找第k大的数，且这个第k大的数是两个数组的中位数。我们虽然不能直接将两个数组合并，但是，由于两个数组都是有序数组，所以当我们取每个数组的前k/2个数时，会出现两种情况，第一个数组的第k/2个数小于第二个数组的第k/2个数，或者第一个数组的第k/2个数大于第二个数组的第k/2个数，我们拿前者的情况举例：当第一个数组的第k/2个数小于第二个数组的第k/2个数时，意味着第k个数也就是本题的中位数肯定不在这第一个数组的前k/2个数中，因此可以排除，为什么呢？因为我们取的是两个数组的分别的前k/2个数，所以这两个“前k/2个数”都加起来撑死也就是前k个数，而当第一个数组的第k/2个数小于第二个数组的第k/2个数时，第一个数组的前k/2个数必然包含在了第二个数组的前k/2个数中，这就好比一个有序数组的最大的那个数比另一个有序数组最大的数还要小，那么前一个数组必然是包含在另一个数组中的，既然两个数组“前k/2个数”的量都加起来也不超过k，且又前一个数组的前k/2个数包含在另一个数组的前k/2个数中，所以前一个数组的那前k/2个数可以大胆舍去。

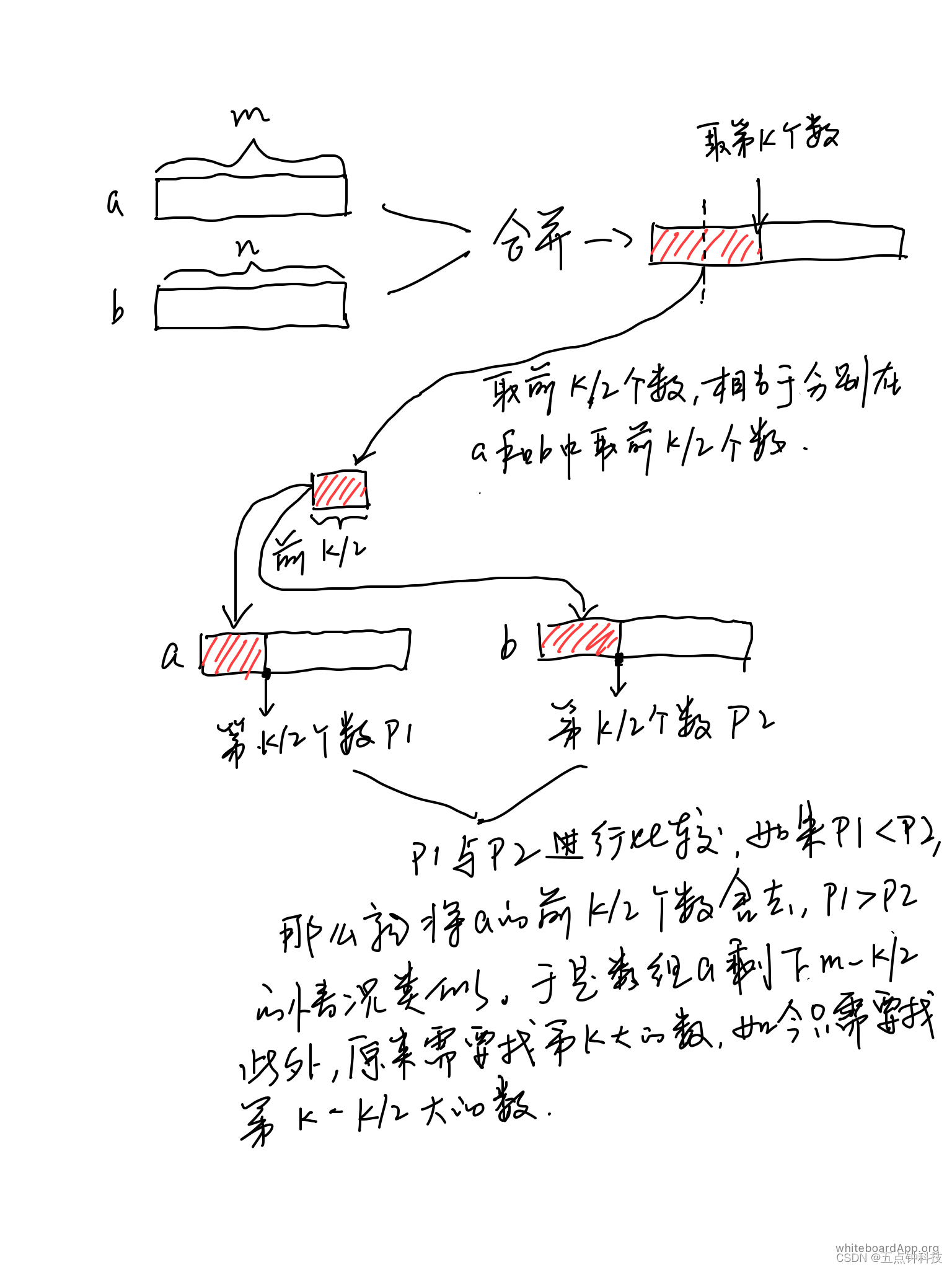举个例子：a数组为[1, 3, 5, 7, 9]，b数组[2, 4, 6, 8]，要取这两个数组的中位数，先看下这两个数组的长度和为奇数，所以中位数所在的位置为(5+4)/2=4，即k为4，现在取a数组的前2个数[1, 3]与b数组的前两个数[2, 4]，由于3<4，那么1和3可以完全排除，因为纵使[1, 3]+[2, 4]=[1, 2, 3, 4]，其数组长度也不超过k，再不济也有个4顶在最后头。

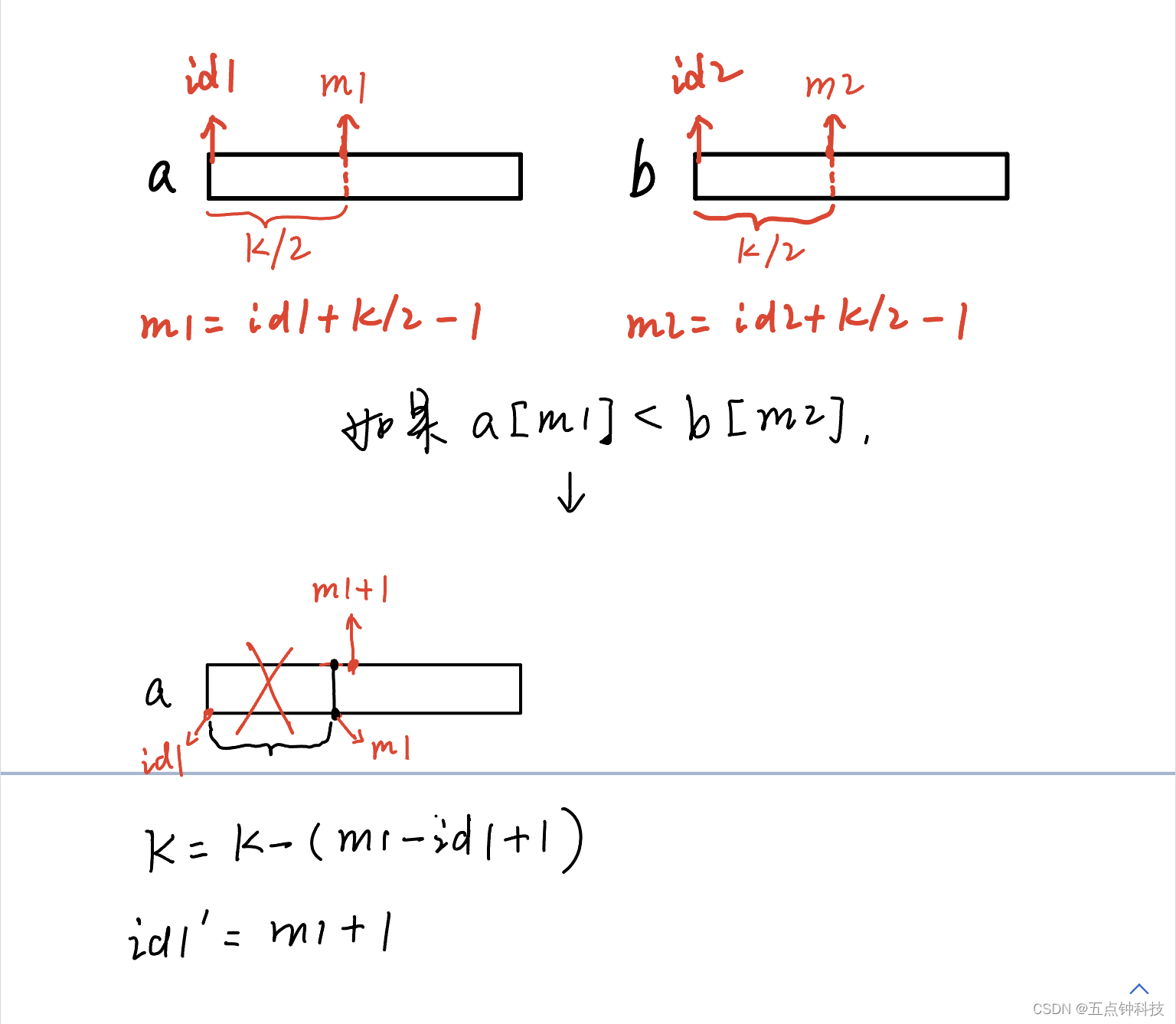
在本题中，我们设定id1和id2两个指针永远指向数组a和b的开头，那么每次找到两个数组的第k/2个数即为id1+k/2-1、id2+k/2-1：

【代码】

def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:
        if not nums1:
            return nums2[len(nums2)//2] if len(nums2)%2 else (nums2[len(nums2)//2-1] + nums2[len(nums2)//2])/2
        if not nums2:
            return nums1[len(nums1)//2] if len(nums1)%2 else (nums1[len(nums1)//2-1] + nums1[len(nums1)//2])/2
        
        m, n = len(nums1), len(nums2)

        def findkth(k):
            id1, id2 = 0, 0
            
            while True:
                # 当某个数组被删完了，那么中位数就在另一个数组中
                if id1 == m:
                    return nums2[id2 + k - 1]
                if id2 == n:
                    return nums1[id1 + k - 1]
                # 此时只需要寻找第1小的数即可
                if k == 1:
                    return min(nums1[id1], nums2[id2])

                m1 = min(id1+k//2-1, m-1)
                m2 = min(id2+k//2-1, n-1)
                if nums1[m1] < nums2[m2]:
                    k = k - (m1 - id1 + 1)
                    id1 = m1 + 1
                else:
                    k = k - (m2 - id2 + 1)
                    id2 = m2 + 1
        size = m + n
        if size % 2:
            return findkth((size+1)//2)
        else:
            return (findkth(size//2+1)+findkth(size//2)) / 2